If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Code Based Positioning (SPS)
| Fundamentals | |
|---|---|
| Title | Code Based Positioning (SPS) |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
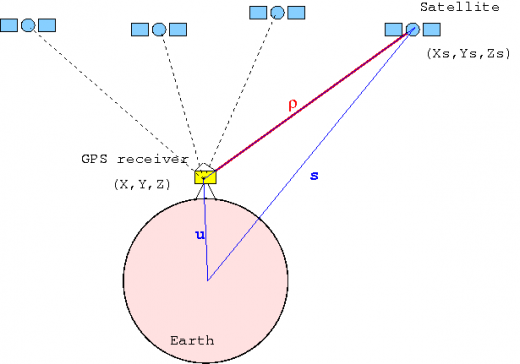
The target is to determine the receiver coordinates [math]\displaystyle{ {\mathbf r}=(x,y,z) }[/math] and clock offset [math]\displaystyle{ \delta t }[/math] from pseudorange measurements [math]\displaystyle{ R^j }[/math] of at least 4 satellites in view. The positioning principle is based on solving a geometric problem from the measured ranges to the satellites, with known coordinates. The satellite coordinates can be computed from the broadcast message, which also provides all necessary information for the measurements modelling for the Standard Positioning Service (SPS).
From the code pseudorange measurements [math]\displaystyle{ R^j }[/math] for, at least, four satellites (see GNSS Measurements Modelling and Instrumental Delay),
- [math]\displaystyle{ R^j=\rho^j+c(\delta t-\delta t^j)+T^j+\hat{\alpha}\, I^j+TGD^j+\mathcal{M}^j+{\boldsymbol \varepsilon}^j \qquad \mbox{(1)} }[/math]
The following measurement equations system can be written, neglecting the multipath and receiver noise terms:
- [math]\displaystyle{ \begin{array}{r} R^j-D^j\simeq \sqrt{(x^j-x)^2+(y^j-y)^2+(z^j-z)^2}+c\,\delta t\\[0.3cm] j=1,2,...,n~~~~ (n \geq 4)\\ \end{array} \qquad \mbox{(2)} }[/math]
where the left side equations contain the measurements [math]\displaystyle{ R^j }[/math] and all modeled terms [math]\displaystyle{ \left ( D^j=-c\,\delta t^j+T^j+\hat{\alpha}\,I^j+TGD^j \right ) }[/math] (see Clock Modelling, Tropospheric Delay, Klobuchar Ionospheric Model, and Instrumental Delay).
The right side contains the four unknown parameters: The receiver coordinates [math]\displaystyle{ (x,y,z) }[/math] and the receiver clock offset [math]\displaystyle{ \delta t }[/math].
The previous equation (2) defines a non linear system, which a usual resolution technique consists of linearising the geometric range [math]\displaystyle{ \rho }[/math] in the neighbourhood of a point [math]\displaystyle{ (x_0,y_0,z_0) }[/math] corresponding to an approximate receiver position.
Then, linearising the satellite-receiver geometric range
- [math]\displaystyle{ \rho^j(x,y,z)=\sqrt{(x^j-x)^2+(y^j-y)^2+(z^j-z)^2} \qquad \mbox{(3)} }[/math]
at the approximative solution [math]\displaystyle{ {\mathbf r}_0=(x_0,y_0,z_0) }[/math], one obtains:
- [math]\displaystyle{ \rho^j=\rho_0^j+\frac{x_0-x^j}{\rho_0^j} dx +\frac{y_0-y^j}{\rho_0^j} dy+\frac{z_0-z^j}{\rho_0^j}dz \qquad with \qquad dx=x-x_0; dy=y-y_0;dz=z-z_0 \qquad \mbox{(4)} }[/math]
Substituting (4) into (2) we can rewrite the measurement equations as a linear system (where [math]\displaystyle{ R^j }[/math] can be whatever, smoothed or unsmoothed code):
- [math]\displaystyle{ \begin{array}{r} R^j-\rho_0^j-D^j=\frac{x_0-x^j}{\rho_0^j}dx +\frac{y_0-y^j} {\rho_0^j} dy+\frac{z_0-z^j}{\rho_0^j} dz+c\,\delta t\\ \\ j=1,2,...,4~~~~(n \geq 4) \end{array} \qquad \mbox{(5)} }[/math]
The previous navigation equation system [footnotes 1] is written in matrix notation as:
- [math]\displaystyle{ \left[ \begin{array}{l} R^1-\rho_0^1-D^1\\ \vdots\\ R^n-\rho_0^n-D^n \end{array} \right] = \left( \begin{array}{cccc} \frac{x_0-x^1}{\rho_0^1}& \frac{y_0-y^1}{\rho_0^1}& \frac{z_0-z^1}{\rho_0^1} & 1\\ \vdots&\vdots&\vdots\\ \frac{x_0-x^n}{\rho_0^n}& \frac{y_0-y^n}{\rho_0^n}& \frac{z_0-z^n}{\rho_0^n} & 1\\ \end{array} \right) \left[ \begin{array}{l} dx\\ dy\\ dz\\ c\,\delta t \end{array} \right] \qquad \mbox{(6)} }[/math]
In general, an over-dimensioned system is obtained (for [math]\displaystyle{ n \gt 4 }[/math]), which can be solved using the Least Squares adjustment.
After solving the equations system (6), the improved estimate of the receiver coordinates is:
- [math]\displaystyle{ \begin{array}{l} \left[ \begin{array}{l} x\\ y\\ z\\ \end{array} \right] =\left[ \begin{array}{l} x_0\\ y_0\\ z_0\\ \end{array} \right] + \left[ \begin{array}{l} dx\\ dy\\ dz\\ \end{array} \right] \end{array} \qquad \mbox{(7)} }[/math]
The equations (2) can be linearised again about these new estimates (7) of the receiver position, and the solution can be iterated until the change between two consecutive iterations is under a given threshold. Typically, the iterations converge quickly, in few iterations, even if starting with [math]\displaystyle{ (x_0,y_0,z_0)=(0,0,0) }[/math], i.e., the earth's centre.
The equations (6) will be named Navigation Equation System and can be written in compact form as:
- [math]\displaystyle{ {\mathbf Y}={\mathbf G}\,{\mathbf X} \qquad \mbox{(8)} }[/math]
where the vectors and matrix involved can be defined as:
- Prefit-residuals: Y is a ([math]\displaystyle{ n \times 1 }[/math]) vector containing the residuals between the measured and predicted pseudoranges, "before fitting" the parameters [math]\displaystyle{ (dx,dy,dz, \delta t) }[/math] to the linear model.
- Geometry matrix: G is a ([math]\displaystyle{ n \times 4 }[/math]) matrix containing the receiver-satellite geometry [footnotes 2]. The first three elements of each row (j = 1,...,n) are the components of the unitary line-of-sight-vector [math]\displaystyle{ {\boldsymbol \rho}= -\frac{(x_0-x^j,y_0-y^j,z_0-z^j)}{|| (x_0-x^j,y_0-y^j,z_0-z^j)||} }[/math].
- Unknown parameters: X is a ([math]\displaystyle{ 4 \times 1 }[/math]) vector containing the deviation [math]\displaystyle{ (dx,dy,dz) }[/math] between the approximated and the true coordinates and the receiver clock offset [math]\displaystyle{ \delta t }[/math].
For more information, please go to the article
Notes
- ^ Strictly speaking, this system corresponds to the case where satellite coordinates at emission time have been calculated using pseudorange algorithm described in Satellite Coordinates Computation. In case of using the purely geometric algorithm of Satellite Coordinates, the elements of the associated matrix (design matrix or Jacobian) varies slightly.
- ^ The matrix [math]\displaystyle{ {\mathbf G} }[/math] can be computed in the ENU coordinates instead of XYZ as in (6). In this local system the rows are [math]\displaystyle{ [\cos el^i \sin az^i, \cos el^i \cos az^i, \sin el^i, 1] }[/math], where [math]\displaystyle{ el^i }[/math] and [math]\displaystyle{ az^i }[/math] are the elevation and azimuth angle of the satellite [math]\displaystyle{ i }[/math] observed from the receiver position (please refer to Transformations between ECEF and ENU coordinates for further details)