Carrier Phase Ambiguity Fixing

Fundamentals
Title	Carrier Phase Ambiguity Fixing
Author(s)	J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain.
Level	Intermediate
Year of Publication	2011

The carrier phase measurements are much more precise than the code pseudorange measurements (typically, about two orders of magnitude), but they contain the unknown ambiguities (B), (see Linear observation model for PPP). If such ambiguities are fixed, thence the carrier phase measurements become as unambiguous pseudoranges, but accurate at the level of few millimetres.

Double differenced ambiguity fixing

In this article the carrier ambiguities will be considered in double differences between pairs of receivers and satellites. This is done in order to cancel out the fractional part of the ambiguities ([math]\displaystyle{ b_{rec} }[/math], [math]\displaystyle{ b^{sat} }[/math]), being the remaining ambiguities integer number of wavelengths. That is, given

[math]\displaystyle{ B_{rec}^{sat}=\lambda \,N_{rec}^{sat}+b_{rec}+b^{sat} \qquad \mbox{(1)} }[/math]

the double differences, regarding to a reference receiver and satellite, yield:

[math]\displaystyle{ \Delta \nabla B_{rec}^{sat}=B_{rec}^{sat}-B_{{rec}_{_0}}^{sat}-(B_{rec}^{{sat}_{_0}}-B_{{rec}_{_0}}^{{sat}_{_0}})=\lambda \,\Delta \nabla N_{rec}^{sat} \qquad \mbox{(2)} }[/math]

where the satellite and receiver ambiguity terms ([math]\displaystyle{ b_{rec},b^{sat} }[/math]) cancel-out.

• Carrier phase ambiguity fixing with two frequencies

• Carrier phase ambiguity fixing with three frequencies

Undifferenced Ambiguity Fixing

The double-differenced ambiguities between pairs of satellites and receivers are integer numbers of wavelengths, see equation (2). Indeed, the fractional part cancels in such double-differences.

[math]\displaystyle{ \nabla \Delta b_{rec}^{sat}=0 \qquad \mbox{(3)} }[/math]

An immediate consequence of previous equation (3) is the split of the fractional part of the ambiguities (for each satellite-receiver arch) in two independent terms, one of them linked only to the receiver and the other only to the satellite.

[math]\displaystyle{ \nabla \Delta b_{rec}^{sat}=0 \Longleftrightarrow b_{rec}^{sat}=b_{rec}+b^{sat} \qquad \mbox{(4)} }[/math]

Notice that (4) means that fractional parts of the ambiguity ([math]\displaystyle{ b_{rec} }[/math] and [math]\displaystyle{ b^{sat} }[/math]) are not linked to a specific satellite-receiver arc, but [math]\displaystyle{ b^{sat} }[/math] depends only of satellite (and it is common to all carrier measurements of receivers tracking this satellite) and [math]\displaystyle{ b_{rec} }[/math] depends only to the receiver (and it is common to all satellites tracked by a given receiver).

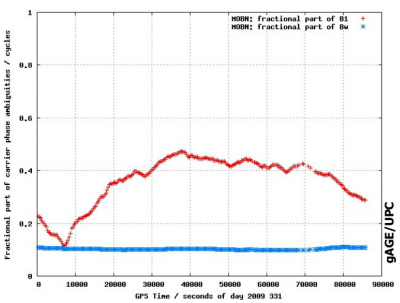
The fractional part of the wide-lane ambiguity can be easily estimated from the Melbourne-Wübbena combination, because it is uncorrelated from other parameters in the navigation filter (see figure 1, in blue ). While the fractional part of the short-lane ambiguity (i.e., [math]\displaystyle{ b_1 }[/math]) can be added to satellite and receiver clock. This approach leads to the so called Phase Clocks [Laurichesse and Mercier, 2007] , which are different from the code clock (i.e., not consistent with the code clock)

Other, more straightforward approach, is to consider such fractional part of ambiguities as Carrier Phase Instrumental Delays , and to remove them using accurate determinations of such values, computed from a receiver network [Juan et al., 2010] . Indeed, the Carrier Instrumental Delays or fractional part of ambiguities ([math]\displaystyle{ b_{rec} }[/math] and [math]\displaystyle{ b^{sat} }[/math]) can be estimated from a global network of permanent stations, after fixing the double-differenced ambiguities [math]\displaystyle{ \nabla \Delta B_{rec}^{sat}=\lambda\, \nabla \Delta N_{rec}^{sat} }[/math] between satellites and receivers. As it is shown in figure 1 theses estimates are stable enough to be broadcast to the users as low varying parameters.

Figure 1: Fractional part of ambiguities for GPS satellite PRN19 (left) and receiver MOBN (right). The Wide-lane is shown in blue and the [math]\displaystyle{ L1 }[/math] in red. The figures are from [Juan et al., 2010] . Vertical axis is in cycles and horizontal in seconds of day. The pattern in the figures is due to the correlations with the other parameters in the filter, mainly the satellite clocks

frameless

frameless

Thence, having accurate determinations of such parameters, the user can remove this fractional part and fix the remaining ambiguity as an integer number. This can be done in a similar way as double differenced mode, but in undifferenced mode; allowing, in this way, to perform real-time ambiguity fixing for PPP, as well.

Notice that, a PPP based ambiguity fixing approach can allow to perform a wold-wide ambiguity fixing, because no baseline limitations applies , improving the PPP accuracy. Nevertheless, as with the PPP, a large convergence time is required for the filter to start the ambiguity fixing (see Carrier phase ambiguity fixing with two frequencies)

Some works focussing into the undiffrenced (or zero-difference) ambiguity fixing are as follows: [Ge et al., 2008] , [Laurichesse and Mercier, 2007], [Collins, 2008] ,[Banville et al., 2008] , [Juan et al., 2010], [Hernandez-Pajares et al., 2010] among others.