If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Instrumental Delay: Difference between revisions
Carlos.Lopez (talk | contribs) (Created page with "{{Article Infobox2 |Category=Fundamentals |Title={{PAGENAME}} |Authors= J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain. |Level=Medium...") |
Carlos.Lopez (talk | contribs) No edit summary |
||
| (18 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Article Infobox2 | {{Article Infobox2 | ||
|Category=Fundamentals | |Category=Fundamentals | ||
|Authors=J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. | |||
|Level=Intermediate | |||
|YearOfPublication=2011 | |||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
Possible sources of these delays are antennas, cables, as well as different filters used in receivers and satellites. These instrumental delays affect both, code and carrier measurements. | Possible sources of these delays are antennas, cables, as well as different filters used in receivers and satellites. These instrumental delays affect both, code and carrier measurements. | ||
The receiver instrumental delay is assimilated in the receiver clock. That is, being common for all satellites, it is assumed as zero and is included in the receiver clock estimate. | The receiver instrumental delay is assimilated in the receiver clock. That is, being common for all satellites, it is assumed as zero and is included in the receiver clock estimate. | ||
Satellite clocks ( | Satellite clocks (broadcast or precise) are referred to the ionosphere-free combination of codes (<math>R_{_{PC}}</math>) and, thence, the instrumental delays cancel in such combination of two frequency signals (see [[Combination of GNSS Measurements]]). | ||
For single frequency users, the satellites broadcast in their navigation messages the Timing Group Delay or Total Group Delay (TGD), which is proportional to the DCB, or interfrequency bias, between the two codes involved in such PC combination <math>K_{P21}\equiv K_{P2}-K_{P1}</math> (see equations ( | For single frequency users, the satellites broadcast in their navigation messages the Timing Group Delay or Total Group Delay (TGD), which is proportional to the Differential Code Bias (DCB), or interfrequency bias, between the two codes involved in such PC combination <math>K_{P21}\equiv K_{P2}-K_{P1}</math> (see equations (6, 11) in the article [[Combining pairs of signals and clock definition]] for further details). | ||
::<math> | ::<math> | ||
TGD_{P1}=\frac{-1}{\gamma_{_{12}}-1} (K_{P2}^ | TGD_{P1}=\frac{-1}{\gamma_{_{12}}-1} (K_{P2}^{sat}-K_{P1}^{sat})=-\hat{\alpha}_1\,K_{P21}^{sat} \qquad \mbox{(1)} </math> | ||
As the instrumental delays | As the instrumental delays cancel in the PC combination, thence, the TGDs for the two associated codes are related by the square of their signal frequencies: | ||
::<math> | ::<math> | ||
| Line 28: | Line 26: | ||
It must be pointed out that the instrumental delay depends not only on the signal frequency but also on the code. For example, there is a DCB between the C1 and P1 GPS codes, and thence, the DCB between the P2 and P1 codes is different to the DCB between P2 and C1 codes. The biases between the C1 and P1 codes, for the different GPS satellites are provided, for instance, by IGS centres. | It must be pointed out that the instrumental delay depends not only on the signal frequency but also on the code. For example, there is a DCB between the C1 and P1 GPS codes, and thence, the DCB between the P2 and P1 codes is different to the DCB between P2 and C1 codes. The biases between the C1 and P1 codes, for the different GPS satellites are provided, for instance, by IGS centres. | ||
Among the navigation message, DCBs are also provided by IGS centres, together with Global Ionospheric | The [[GALILEO General Introduction|Galileo]] navigation messages F/NAV and I/NAV broadcast TGDs for the code on frequency E1, associated to the ionosphere free combinations of codes at the frequencies E5a,E1 and E5b,E1, respectively. No TGDs (nor any ionospheric model) is broadcast in the [[GLONASS General Introduction|GLONASS]] navigation message. | ||
Among the navigation message, DCBs are also provided by IGS centres, together with Global Ionospheric Maps (GIM) files. At this regard, it must be pointed out that there is a correlation between the DCBs and the ionospheric estimates (see [[Combining pairs of signals and clock definition]]). Indeed, the DCBs are associated to the ionospheric model used to compute such values. Thence, the DCBs broadcasted in the GPS navigation message must be used with the [[Klobuchar Ionospheric Model|Klobuchar]] ionospheric model and the DCBs of IGS GIMs with the IONEX files. | |||
::{| | ::{| | ||
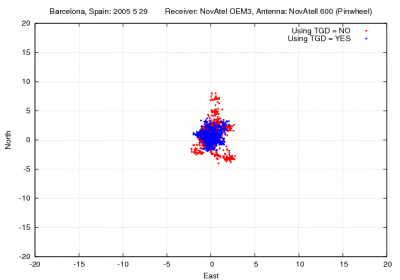
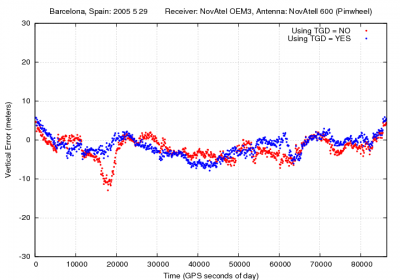
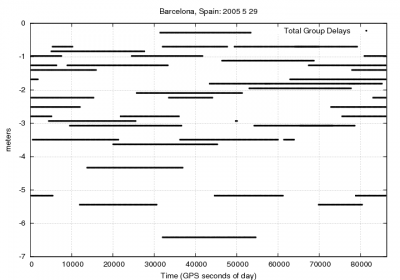
|+align="bottom"|''Figure 1: Total Group Delay: Range and position domain effect '' | |+align="bottom"|''Figure 1: Total Group Delay: Range and position domain effect.'' | ||
| [[File:Instrumental_Delay_H_Nov_tgd.png|none|thumb|400px|frameless]] | | [[File:Instrumental_Delay_H_Nov_tgd.png|none|thumb|400px|frameless]] | ||
| [[File:Instrumental_Delay_V_Nov_tgd.png|none|thumb|400px|frameless]] | | [[File:Instrumental_Delay_V_Nov_tgd.png|none|thumb|400px|frameless]] | ||
|- | |- | ||
| [[File:Instrumental_Delay_Nov_TGD.png |none|thumb|400px|frameless]] | | [[File:Instrumental_Delay_Nov_TGD.png |none|thumb|400px|frameless]] | ||
| '' First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the broadcasted Total Group Delays (TGDs) (equation 1). The variation in range is shown in the second row at left'' | | '' First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the broadcasted Total Group Delays (TGDs) (equation 1). The variation in range is shown in the second row at left.'' | ||
|} | |} | ||
Figure 1 illustrates the values of the GPS P1 code TGDs. Moreover the effect of neglecting such delays in | Figure 1 illustrates the values of the GPS P1 code TGDs. Moreover the effect of neglecting such delays in Single Point Positioning for the horizontal and vertical error components is depicted by comparing the navigation solution using (blue) and not using (red) such TGDs. | ||
Finally, the carrier phase instrumental delays are assimilated in the unknown ambiguities, which are estimated as real numbers (floating ambiguities) when positioning in [[Code and Carrier | Finally, the carrier phase instrumental delays are assimilated in the unknown ambiguities, which are estimated as real numbers (floating ambiguities) when positioning in [[Code and Carrier Based Positioning (PPP)|PPP]]. | ||
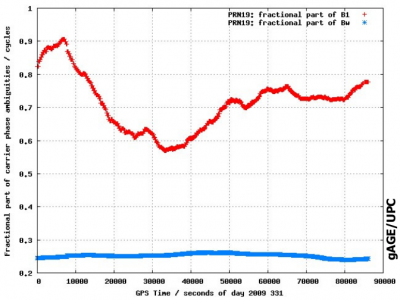
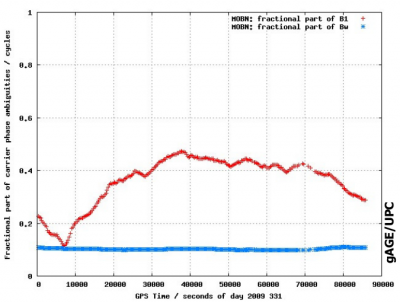
Figure 2 shows the fractional part of the wide-lane and L1 ambiguities <ref>Actually, the residuals of carrier phase instrumental delays module the wavelength</ref>. for a GPS satellite and for a receiver. These carrier phase instrumental delays | Figure 2 shows the fractional part of the wide-lane and L1 ambiguities <ref group="footnotes">Actually, the residuals of carrier phase instrumental delays module the wavelength</ref>. for a GPS satellite and for a receiver. These carrier phase instrumental delays cancel in the double differences between satellites and receivers and, thence, are not needed to know to fix ambiguities in differential mode. Nevertheless, they are needed (the satellite ones) for undifferenced ambiguity fixing, e.g., real-time ambiguity fixing for PPP (see [[Carrier Phase Ambiguity Fixing]]). | ||
::{| | ::{| | ||
|+align="bottom"|''Figure 2: Fractional part of ambiguities for GPS satellite PRN19 (left) and receiver MOBN (right). The Wide-lane is shown in blue and the <math>L1</math> in red.'' | |+align="bottom"|''Figure 2: Fractional part of ambiguities for GPS satellite PRN19 (left) and receiver MOBN (right). The Wide-lane is shown in blue and the <math>L1</math> in red. The figures are from <ref> [Juan et al., 2010] Juan, J., Hernandez-Pajares, M. and Sanz, J., 2010. Precise Real Time Orbit Determination and Time Synchronization (PRTODTS). TN2 & TN3: GPS PRTODTS Design and Validation Documents, v0.0. | ||
ESA report (ESA ITT AO/1-5823/08/NL/AT), ESOC/ESA, The Netherlands.</ref>. Vertical axis is in cycles and horizontal in seconds of day. The pattern in the figures is due to the correlations with the other parameters in the filter, mainly the satellite clocks.'' | |||
| [[File:Instrumental_Delay_sat_frac1.png|none|thumb|400px|frameless]] | | [[File:Instrumental_Delay_sat_frac1.png|none|thumb|400px|frameless]] | ||
| [[File:Instrumental_Delay_rec_frac1.png|none|thumb|400px|frameless]] | | [[File:Instrumental_Delay_rec_frac1.png|none|thumb|400px|frameless]] | ||
|} | |} | ||
For more information see [[GPS C1, P1 and P2 Codes and Receiver Types]] | For more information see [[GPS C1, P1 and P2 Codes and Receiver Types]] | ||
==Notes== | |||
<references group="footnotes"/> | |||
==References== | ==References== | ||
| Line 64: | Line 69: | ||
[[Category:Fundamentals]] | [[Category:Fundamentals]] | ||
[[Category:GNSS Measurements Modelling]] | |||
Latest revision as of 11:33, 23 February 2012
| Fundamentals | |
|---|---|
| Title | Instrumental Delay |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
Possible sources of these delays are antennas, cables, as well as different filters used in receivers and satellites. These instrumental delays affect both, code and carrier measurements.
The receiver instrumental delay is assimilated in the receiver clock. That is, being common for all satellites, it is assumed as zero and is included in the receiver clock estimate.
Satellite clocks (broadcast or precise) are referred to the ionosphere-free combination of codes ([math]\displaystyle{ R_{_{PC}} }[/math]) and, thence, the instrumental delays cancel in such combination of two frequency signals (see Combination of GNSS Measurements).
For single frequency users, the satellites broadcast in their navigation messages the Timing Group Delay or Total Group Delay (TGD), which is proportional to the Differential Code Bias (DCB), or interfrequency bias, between the two codes involved in such PC combination [math]\displaystyle{ K_{P21}\equiv K_{P2}-K_{P1} }[/math] (see equations (6, 11) in the article Combining pairs of signals and clock definition for further details).
- [math]\displaystyle{ TGD_{P1}=\frac{-1}{\gamma_{_{12}}-1} (K_{P2}^{sat}-K_{P1}^{sat})=-\hat{\alpha}_1\,K_{P21}^{sat} \qquad \mbox{(1)} }[/math]
As the instrumental delays cancel in the PC combination, thence, the TGDs for the two associated codes are related by the square of their signal frequencies:
- [math]\displaystyle{ TGD_{P2}=\gamma_{_{12}}\, TGD_{P1} \qquad \mbox{(2)} }[/math]
It must be pointed out that the instrumental delay depends not only on the signal frequency but also on the code. For example, there is a DCB between the C1 and P1 GPS codes, and thence, the DCB between the P2 and P1 codes is different to the DCB between P2 and C1 codes. The biases between the C1 and P1 codes, for the different GPS satellites are provided, for instance, by IGS centres.
The Galileo navigation messages F/NAV and I/NAV broadcast TGDs for the code on frequency E1, associated to the ionosphere free combinations of codes at the frequencies E5a,E1 and E5b,E1, respectively. No TGDs (nor any ionospheric model) is broadcast in the GLONASS navigation message.
Among the navigation message, DCBs are also provided by IGS centres, together with Global Ionospheric Maps (GIM) files. At this regard, it must be pointed out that there is a correlation between the DCBs and the ionospheric estimates (see Combining pairs of signals and clock definition). Indeed, the DCBs are associated to the ionospheric model used to compute such values. Thence, the DCBs broadcasted in the GPS navigation message must be used with the Klobuchar ionospheric model and the DCBs of IGS GIMs with the IONEX files.
Figure 1: Total Group Delay: Range and position domain effect. First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the broadcasted Total Group Delays (TGDs) (equation 1). The variation in range is shown in the second row at left.
Figure 1 illustrates the values of the GPS P1 code TGDs. Moreover the effect of neglecting such delays in Single Point Positioning for the horizontal and vertical error components is depicted by comparing the navigation solution using (blue) and not using (red) such TGDs.
Finally, the carrier phase instrumental delays are assimilated in the unknown ambiguities, which are estimated as real numbers (floating ambiguities) when positioning in PPP.
Figure 2 shows the fractional part of the wide-lane and L1 ambiguities [footnotes 1]. for a GPS satellite and for a receiver. These carrier phase instrumental delays cancel in the double differences between satellites and receivers and, thence, are not needed to know to fix ambiguities in differential mode. Nevertheless, they are needed (the satellite ones) for undifferenced ambiguity fixing, e.g., real-time ambiguity fixing for PPP (see Carrier Phase Ambiguity Fixing).
Figure 2: Fractional part of ambiguities for GPS satellite PRN19 (left) and receiver MOBN (right). The Wide-lane is shown in blue and the [math]\displaystyle{ L1 }[/math] in red. The figures are from [1]. Vertical axis is in cycles and horizontal in seconds of day. The pattern in the figures is due to the correlations with the other parameters in the filter, mainly the satellite clocks.
For more information see GPS C1, P1 and P2 Codes and Receiver Types
Notes
- ^ Actually, the residuals of carrier phase instrumental delays module the wavelength
References
- ^ [Juan et al., 2010] Juan, J., Hernandez-Pajares, M. and Sanz, J., 2010. Precise Real Time Orbit Determination and Time Synchronization (PRTODTS). TN2 & TN3: GPS PRTODTS Design and Validation Documents, v0.0. ESA report (ESA ITT AO/1-5823/08/NL/AT), ESOC/ESA, The Netherlands.