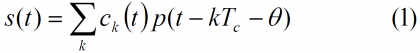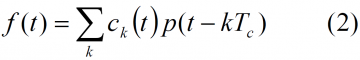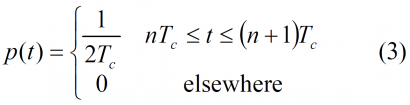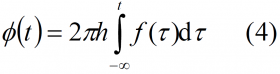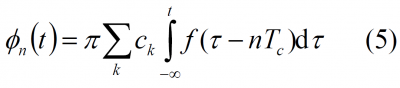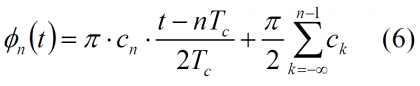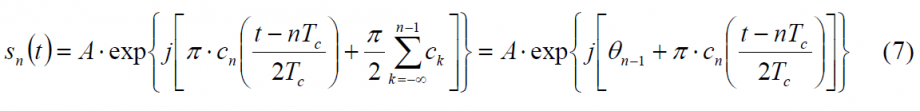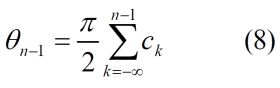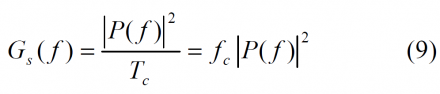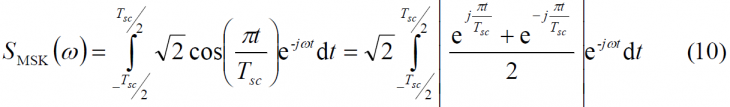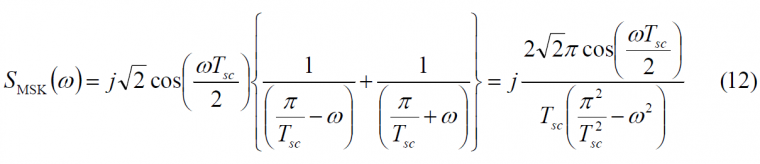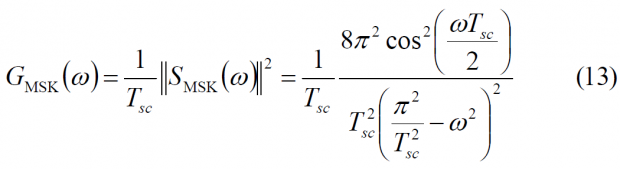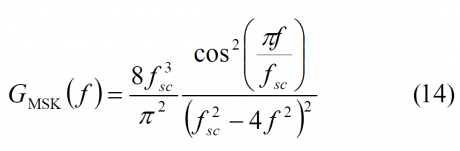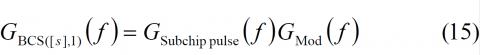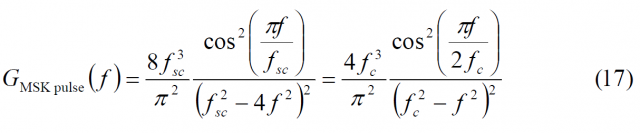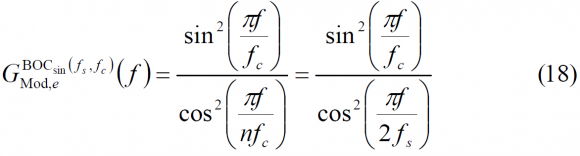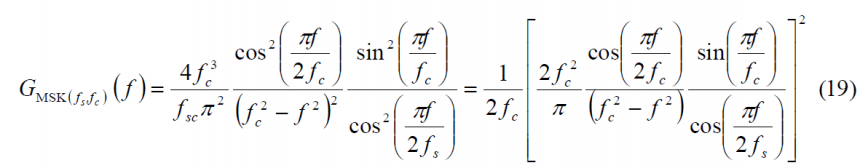Minimum Shift Keying (MSK)

Fundamentals
Title	Minimum Shift Keying (MSK)
Author(s)	J.A Ávila Rodríguez, University FAF Munich, Germany.
Level	Advanced
Year of Publication	2011

The MSK modulation is a constant envelope signal with continuous phase that results from modulating the instantaneous frequency with rectangular pulses. MSK is considered to be a special case of Offset QPSK (OQPSK) with half sinusoidal pulse weighting rather than rectangular. Furthermore, MSK presents lower side lobes than QPSK and OQPSK as shown in [S. A. Gronemeyer and A. L. McBride, 1976] and [H. R. Mathwich et al., 1974] . As one can imagine, this could be of great interest for those navigation bands where the Out of Band emission constraints are stringent as in the case of the C-band between 5010 and 5030 MHz.

Assuming that the PRN codes are ideal and making the same assumptions of previous chapters, the MSK modulation can be seen as a particular case of SMCS with sinusoidal pulse waveform. Moreover, since MSK is a particular case of MCS, all the expressions derived in those articles can also be used for this particular case.

In the MSK modulation the evolution of the phase over the time is linear. Indeed, recalling the general expression of

and keeping in mind that MSK is a frequency modulation, it can be shown that the evolution of the frequency over time adopts the following expression:

where [math]\displaystyle{ c_k \left (t\right ) }[/math] is the PRN code and [math]\displaystyle{ p \left (t\right ) }[/math]is the frequency pulse, defined for period n as follows:

Accordingly, the variation of the phase over the time will adopt the following form:

with . Putting now (2) and (4) together, the evolution of the phase over one period , that is [math]\displaystyle{ nT_c \le t\le \left (n+1 \right ) T }[/math], will be:

which can also be expressed as follows:

Accordingly, the expression of the MSK will be:

with

Taking now the real and imaginary part of (7), the sinusoidal shape of the chip waveform is then observed. Since we assume ideal codes, we only need to work with the chip waveform as described in (9) (refer to Autocorrelation & Power Spectral Density).

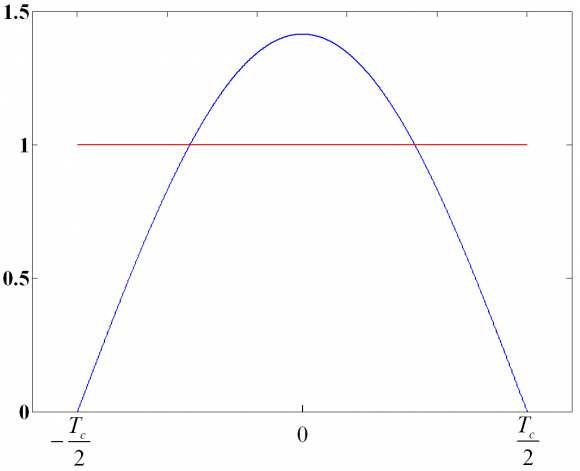
Next figure compares the typical binary pulse with that of MSK:

Figure 1: Binary and MSK chip waveform.

In order the original power of MSK to remain equivalent to that of the ordinary binary signals, the factor [math]\displaystyle{ A = sqrt{2} }[/math] was used in the MSK expression as we can observe. To derive now the PSD according to (9), we calculate first the Fourier Transform of the MSK pulse waveform:

which simplifies to:

As we can recognize, we are defining the spreading waveform in a subchip of length [math]\displaystyle{ T_sc }[/math] where [math]\displaystyle{ T_c = nT_sc }[/math], being [math]\displaystyle{ T_c }[/math] the duration of a chip and n the number of subchips in one chip. Accordingly, this is the Fourier transform of the subchip part and [math]\displaystyle{ f_sc = n f_c }[/math]. This expression can be further simplified yielding:

According to this, the normalized Power Spectral Density of the spreading MSK waveform adopts the following form:

which can also be expressed as follows:.

As we can recognize, this expression perfectly coincides with that derived [S. Pasupathy, 1979] .

Once we have derived the pulse waveform for a cosine shape, any SMCS can be obtained using the general formula obtained in (15).

As an example, in the next lines we derive the expression for a sine-phased [math]\displaystyle{ BOC \left (f_s , f_c \right ) }[/math] with MSK pulses and we will compare it with the original BPSK with MSK pulses. For simplicity in the notation we call [math]\displaystyle{ MSK \left (f_s , f_c \right ) }[/math] to the first one and </math>MSK \left (f_c \right)</math> to the second one. As one can imagine, this notation can be generalized to any BOC or arbitrary BCS signal. It is important to note that in this particular case [math]\displaystyle{ T_sc }[/math] is equal to [math]\displaystyle{ T_c/n }[/math] and [math]\displaystyle{ f_sc = nf_c }[/math] consequently. In addition, it can be shown that [math]\displaystyle{ nf_c = 2f_s }[/math] for the modulating term as it was also the case for the usual BOC modulation. In conclusion, the PSD of MSK-BOC([math]\displaystyle{ f_s }[/math],[math]\displaystyle{ f_c }[/math]) or MSK([math]\displaystyle{ f_s }[/math] , [math]\displaystyle{ f_c }[/math]) for short, will adopt the following form:

where in this particular case:

since [math]\displaystyle{ f_sc = 2f_c }[/math] for the sine-phased MSK-BOC case. On the other hand, for the even case, the modulation spectral term adopts the following form in general:

where n is again the number of subchips in one chip. Thus, multiplying now both terms and normalizing the power to integrate to 1 in an infinite bandwidth yields thus the PSD of the MSK([math]\displaystyle{ f_s }[/math],[math]\displaystyle{ f_c }[/math]):

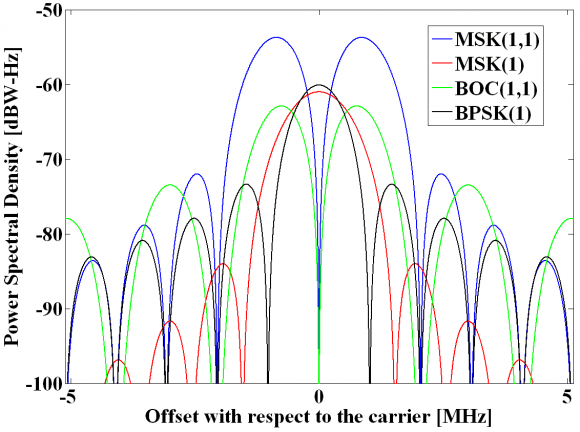
For comparison the PSDs of MSK(1,1), MSK(1), BPSK(1) and BOC(1,1) are shown next:

Figure 2: PSDs of MSK(1,1), MSK(1), BOC(1,1) and BPSK(1).

As we can recognize from the previous figure, for the same chip rate of 1.023 Mcps, MSK(1) has a main lobe that is 1.5 times wider than that of BPSK(1). On the other hand, MSK(1,1) has a main lobe that is as broad as that of BOC(1,1) but with secondary lobes that are half the width. MSK has a very good spectral confinement and provides at the same time constant envelope.

Credits

The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)