If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Sinusoidal Multilevel Coded Symbol (SMCS) Signals
| Fundamentals | |
|---|---|
| Title | Sinusoidal Multilevel Coded Symbol (SMCS) Signals |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
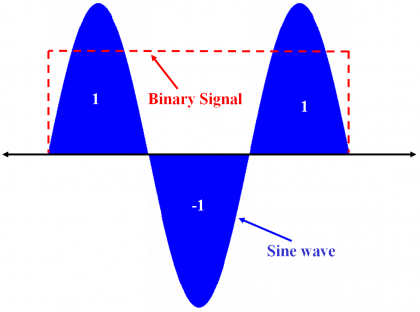
In this article we will discuss a family of signals that results from modulating each subchip of the generation vector [math]\displaystyle{ \bar s }[/math] with a sinusoidal function. Such signals receive the name of Sinusoidal Offset Carrier signals or SOC for short if the sinusoidal function is modulated by a binary code. The alternative use of Linear Offset Carrier or LOC is also often observed in the literature. As we can recognize, SMCS can be interpreted as a particular MCS that uses subchip pulses with sinusoidal shape. Accordingly, the equation (1) could be applied. The original idea to use this signal for satellite navigation was presented in [J. W. Betz, 1999][1] and has been further developed in [J. Winkel, 2002][2]. The SOC signal can be defined as follows:
where n corresponds to the number of periods of the sine wave that are contained in each code bit and the factor [math]\displaystyle{ sqrt{2} }[/math] was introduced to normalize the power to 1. Furthermore, [math]\displaystyle{ c_k }[/math] refers to the subchips modulating the chip waveform. It is important to note that the chip waveform is defined by the sequence of subchips that forms it according to the generation vector [math]\displaystyle{ \bar s }[/math] (please refer to Multilevel Coded Spreading Symbols (MCS) for further details on the generation of vector [math]\displaystyle{ \bar s }[/math] ).
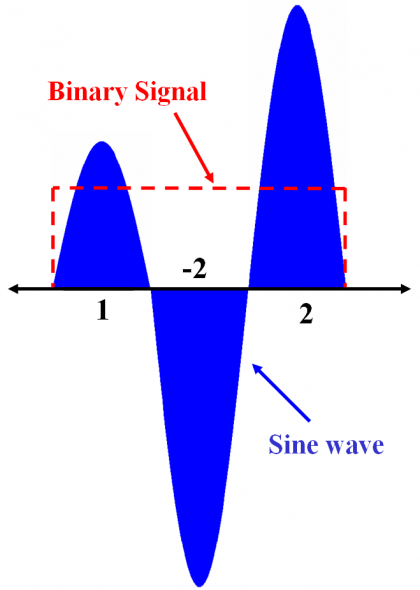
While this definition applies only to the case of Offset Carrier Chips ([1, -1, 1, -1, …]), one can imagine a generalized version for Binary Coded Symbols. We will define these signals thus in general as Sinusoidal Binary Coded Symbols or SBCS for short. Next figure shows an example of SBCS with vector [1,-1,1].
As we can clearly recognize, there exists the same relationship between SBCS signals and SOCs as there was between BCS and BOC. In fact, the SOC signal that we defined above is a particular case of the SBCS modulation that we have just described. According to this, if we talk about SBCS([1,-1],1) and SOC(1,1) we are indeed referring to the same signal.
In addition, it is important to mention that since, as we know from theory, the square-wave contains tones at odd frequencies multiple of the elemental frequency, the SOC signal can be interpreted qualitatively as a BOC signal that is filtered to have only the first tone.
To summarize, we can conclude that this idea can be understood as a particular case of Multilevel Coded Spreading Symbols (MCS) modulation with a pulse waveform of sinusoidal form.
Next figure shows another example.
Furthermore, it is important to note that unlike in the most straightforward definition of the SOC modulation, the factor accompanying the sine signal will not be in general [math]\displaystyle{ sqrt{2} }[/math] and will depend on the particular symbol sequence. In fact, the factor has the mission to normalize the power of the signal to unity.
Related articles
References
- ^ [J. W. Betz, 1999] J. W. Betz, The offset carrier modulation for GPS modernization, in Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 1999, pp. 639–648, January 1999, San Diego, California, USA.
- ^ [J. Winkel, 2002] J. Winkel, Modeling and Simulating Generic GNSS Signal Structures and Receiver in a Multipath Environment, Ph.D. Thesis, University FAF Munich, Neubiberg, Germany.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)