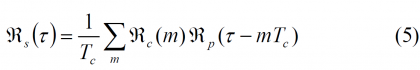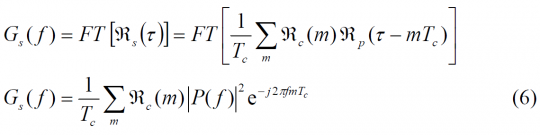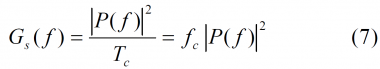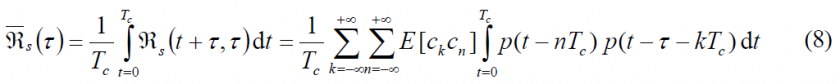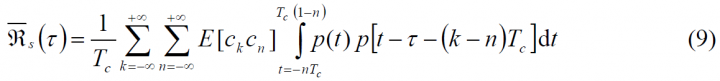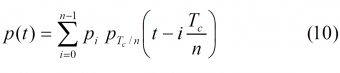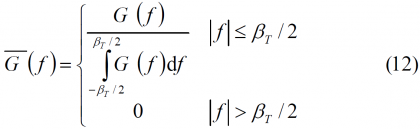If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Autocorrelation & Power Spectral Density
| Fundamentals | |
|---|---|
| Title | Autocorrelation & Power Spectral Density |
| Author(s) | J.A. Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
Autocorrelation and Power Spectral Density
When dealing with DSSS signals, two very important characteristics are the autocorrelation function and the power spectrum, since they determine the navigation performance of a signal.
Let us assume that our signal is stationary in wide sense and can be expressed as follows:
where θ is a uniformly distributed variable within [math]\displaystyle{ \left [ 0, T_c \right ) }[/math]. As we know, we say that a signal is stationary in wide sense when the first and second moments do not change with the time. This means in other words:
- and
what is equivalent to saying that the mean is constant and the correlation function does only depend on the difference of time between t1 and t2. It must be noted that [math]\displaystyle{ \Delta }[/math] does not vary with time representing thus an initial random shift in the signal that remains constant over time.
Assuming that our signal fulfils the above described properties, we can show that the autocorrelation function is defined thus as:
since the signal is assumed to be stationary. We can further simplify this expression as:
According to this, the power spectral density of s(t) can be obtained from the Fourier Transform of the autocorrelation of s(t), [math]\displaystyle{ \mathfrak{R}_S(\tau) }[/math] derived above, according to:
where P(f) is the Fourier Transform of the waveform p(t). Moreover, the signal was assumed to be real. Assuming now that the PRN codes show ideal properties – that is random, non periodic, identically distributed, equiprobable and independent – then the crosscorrelation can be approximated as [math]\displaystyle{ E \left \{C_k C_n^* \right \} \approx \delta_{kn} }[/math] or what is equivalent [math]\displaystyle{ \mathfrak{R}_C (m) \approx \delta (m) }[/math], and the power spectrum density simplifies to:
For further justification on the use of the Dirac delta in the previous lines, refer to [M. J. Lighthill, 1958][1] where additional arguments are provided. This expression is of great value since it will allow us to calculate the power spectral density of the different signals we will analyze in our work. Indeed, if we can express all the different signal waveforms by means of their chip waveform we will be able to use this expression to obtain the power spectral density. As we will mention later, this is not possible in a general case but fortunately it is a good approximation for most of the cases.
Moreover, real DSSS signals are not stationary in wide sense. Thus, it is better to work with the average autocorrelation function in general. According to this, the average autocorrelation function can be expressed as follows:
where [math]\displaystyle{ p(t) }[/math] was assumed to be real. This expression can be further developed as follows:
where [math]\displaystyle{ \mathfrak{R}_S (\tau) }[/math] was derived some lines above in (5). Again, assuming the codes show ideal properties, the crosscorrelation will be [math]\displaystyle{ E \left \{C_k C_n \right \} \approx \delta_{kn} }[/math].
Observing the equation above we can clearly recognize that the average autocorrelation function for a DSSS signal is equal to the aperiodic autocorrelation function of the chip waveform under the assumption that the codes are ideally random. This is a very important result since we will base most of the derivations of this chapter on it. Later we will relax this strong assumption on the ideality of the codes and see how the results differ when actual non-ideal codes are employed to modulate the chip waveform.
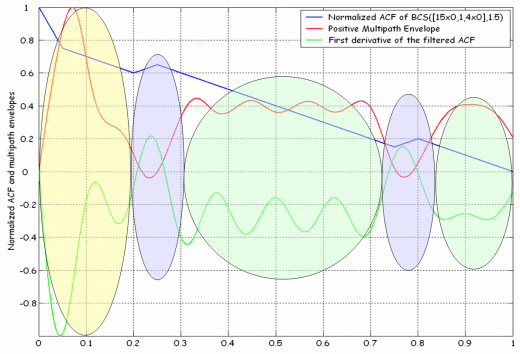
Once we have derived the expression for the average autocorrelation function (ACF) of a generic DSSS signal, the first question that arises is how the ACF of an ideal waveform should look like in order to be able to accomplish the best possible precise ranging in satellite navigation. As shown in the following figure, the sharper the peak of the autocorrelation function, the more precise the ranging will be with this waveform. Similar works with band-limited signals have been carried out by [F. Antreich and J. A. Nossek, 2007][2]. An E-L discriminator with 0.1 chips of spacing was employed in this example.
The following conclusions can be obtained from the figure above:
- If an E-L tracker is used, there is a high correlation between the multipath performance of a signal and the first derivative of the autocorrelation function.
- The first plateau (in yellow in the figure) or peak of the multipath envelopes is determined by the spacing of the correlator, by the location of the first secondary peak of the ACF and by the slope of the ACF around the main peak.
- The steeper the slope, the better as it reduces the plateau of the multipath envelopes.
- The nearer to the main peak the inversion of the sign of the secondary peak takes place, the better the multipath since the envelope is obligated to fall to 0 (blue).
- An inversion in the slope of the ACF forces the multipath envelopes to pass through zero. Therefore the closer this inversion is to the main peak, the lower the multipath envelopes will be for short multipath (blue).
- No inversion in the slope makes the multipath envelope to move/keep the height of the plateau (green).
- A change in the slope (not in the sign) makes the multipath envelope tend to a new plateau (yellow).
- The sensitivity of a signal to multipath is lower the higher the chipping rate is since the effect of multipath is invisible to the receiver once the multipath signal comes from a given distance that depends on the particular discriminator.
As a conclusion, the steeper the main peak of the autocorrelation and the more ripples this has, the better the potential performance of the signal will be. The counterpart is that the higher the number of elements in one chip, the higher will be the number of ripples of the autocorrelation so that the receiver might have problems to track or acquire the correct peak.
From (9) we can deduce that a signal with a sharp autocorrelation function can be generated by selecting p(t) with good aperiodic correlation properties. In the ideal case, p(t) should be a Dirac delta.
The expression for the chip waveform p(t) is given by
According to this, each chip waveform is broken up into n rectangular pulses of duration [math]\displaystyle{ T_c / n }[/math] with amplitudes defined by the sequence {pi}. Furthermore, [math]\displaystyle{ P_{T_c / n}(t) }[/math] represents the shape of each of the rectangular pulses the chip waveform is broken up into. In principle {pi}, defined as MCS (Multilevel Coded Symbols) sequence in this thesis, could adopt any real value, although for satellite navigation a bi-phase signal with {pi}[math]\displaystyle{ \left \{p_i \right \} \in \left \{+1, -1 \right \} }[/math] is typical.
Finally, the power spectral density of the DSSS signal can be obtained as the Fourier Transform of the autocorrelation function derived above, according to
The interesting thing about the derivations above is that since the autocorrelation function was expressed in a tailored way using the general formulation of (10), the power spectrum can also be tailored shaping thus the attributes of the desired signal as we wish. This is of great interest for navigation applications, since on the one hand, as we mentioned above, we are interested in having autocorrelation functions as sharp as possible around the main peak, while at the same time a broad spectrum with minimum overlapping with other signals would minimize mutual interference with other existing signals in the band.
One final but important comment is that normally it is assumed that the transmitted GNSS interfering signals are band limited at the satellite transmitter. Thus, if we assume an ideal transmit filter of rectangular form (also referred to as brick-wall filter in this thesis) with bandwidth T, the normalized power spectral density of unit power within the satellite transmission bandwidth should be expressed as follows:
References
- ^ [M. J. Lighthill, 1958] M. J. Lighthill, Introduction to Fourier Analysis and Generalized Functions, New York, Cambridge University Press, 1958
- ^ [F. Antreich and J. A. Nossek, 2007] F. Antreich and Josef A. Nossek, On Chip Pulse Shape Design for Global Navigation Satellite Systems, Second CNES Workshop on Galileo Signals and Signal Processing, 24-25 April 2007, ESTEC, Noordwijk, The Netherlands.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)