Time References

Fundamentals
Title	Time References
Author(s)	J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain.
Level	Basic
Year of Publication	2011

Introduction

Our everyday life follows the alternation of day and night, and seasons of year, and then the initial conception of time was based on the motion of sun. Nevertheless, as science and technology evolved, more precise uniform and well-defined time scales were needed.

Several time references are currently adopted, based on the different periodic processes associated, such as earth rotation, celestial mechanics or transitions between energetic levels in atomic oscillators. Table 1 summarises the different used time systems as well their associated periodic process.

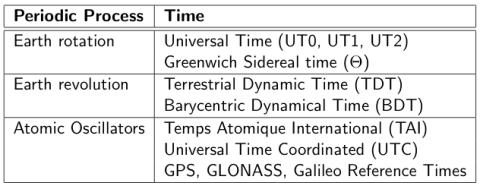Table 1: Different time systems (from [Hofmann-Wellenhof et al., 2003])

For information on the time references used in the different GNSS, please refer to Time References in GNSS.

Description

Universal and Sidereal times are associated with earth daily rotation. Universal time (solar time) uses the sun as a reference. Sidereal time uses the Vernal Equinox (the Aries point). This leads to the fact that, in a year, both times differ by 24 hours (one lap) and, thence, the sidereal day is shorter than the solar day by 3^m 56^s.4, see section Sidereal Time. That is:

1 mean sidereal day = 1 mean solar day − 3^m56^s.4

Universal time UT (UT0, UT1, UT2) is not completely uniform. So, the Atomic Time TAI was introduced to achieve a more uniform time scale. TAI and UT accumulate a drift along time. Due to this, UTC was defined, which is an atomic time that keeps itself within 0.9 seconds from UT1. It is done by the systematic introduction of a certain number of seconds called Leap Seconds. This causes that, along time, the difference between UTC and TAI varies in integer leaps of 1 second. UTC is generated by the Bureau International des Poids et Mesures (BIPM), located in Paris. The leap seconds are determined by the International Earth Rotation and Reference Systems Service (IERS).

UTC is obtained from about 250 cesium clocks and hydrogen masers located at about 65 different laboratories, distributed around the world, and applying a set of algorithms to assure an uniform time. It is not determined in real time, but generated with a delay of about half month. Real-time estimates of UTC are computed and provided by different centres, as the UTC(USNO), from the United States Naval Observatory (USNO), the UTC(NIST), from the National Institute of Standards and Technology (NIST), and the UTC(SU) from Russia (SU stands for the former Soviet Union) or, in general, UTC(k) as a realization of UTC by a given laboratory k, see [Lewandowski et al., 2006]. ESA’s timing capability built to support the validation of the Galileo timing performances also provides an UTC estimate, formally known as UTC (ESTEC). Recently this estimate is also being providing as a contribution to the generation of the overall UTC.

Please find more detailed information in Time Systems.

Time References Relationship

The following relations are met (see details in article appendix Transformations between Time Systems).

[math]\displaystyle{ \begin{array}{lcl} TAI\,=\,TDT\,-\,32^s.184 \\ TAI\,=\,UTC\,+\,1^s *\,n \\ UTC\,=\,UT1\,+\,dU\, T\, 1,\, where\, |dU T 1|\, \lt \, 0^s.9. \end{array} \qquad \mbox{(1)} }[/math]

where n is the number of Leap Seconds introduced for a given epoch (e.g., 01/Jul/97 n = 31, 01/Jan/99 n = 32, 01/Jan/06, n = 33, 01/Jan/09 n = 34).

Figure 1: UT1-UTC and leap seconds adjustments (data from USNO)

Calendar Systems

In order to facilitate calculations for long time intervals, the Julian date is used (from Julio Scalier). The 1st of January of 4713 BC is considered as the reference epoch and, starting from there, days are counted in a correlative way. The Julian Day (JD) starts at 12^h of the corresponding civil day (i.e.: 6^d.0 January 1980 = JD 2444244.5). The current reference standard epoch for the scientific community is:

[math]\displaystyle{ J2000.0 = 1^d.5\, January\, 2000\, =\, JD\, 2\,451\,545.0 \qquad \mbox{(2)} }[/math]

The Modified Julian Day (MJD) is also used, which is obtained subtracting 2 400 000.5 days from the Julian Day.

The following expression provides the Julian Day from a civil date (YYMMDDUT):

[math]\displaystyle{ \begin{array}{ll} ~~JD=int[365.25 * y]+ int[30.6001 * (m+1)] + DD +\frac{UT (hours)}{24}+1720981.5 \\[0.2cm] ~\mbox{where:}\\[0.2cm] ~~ \qquad y=YY-1,~~ m=MM+12,~~ MM\leq 2 & \\ ~~ \qquad y=YY,~~ m=MM,~~ MM\gt 2\\ \end{array} \qquad \mbox{(3)} }[/math]

From Julian Day, and taking into account that GPS reference data (6^d.0 January 1980) corresponds to JD 2 444 244.5, one immediately obtains the GPST. Thence, taking module 7, the GPS week is found.

The inverse transformation is given in equation (3) in Julian Date.

As another example, the 3 hours (Moscow Time) on January 1st 1975 (21 hours GMT December 31st, 1974) used by GLONASS as a reference time in some computations, corresponds to JD 2 442 413.375 (GMT).

Greenwich Mean Sidereal ([math]\displaystyle{ \theta_{_G} }[/math]) Time and Universal Time are related by the following expression (see equation (4) in CEP to ITRF):

[math]\displaystyle{ \begin{array}{ll} ~~\theta_{_G}=r\cdot UT1+6^h41^m50^s_{\cdot}5481+8\,640\,184^s_{\cdot}812\,866\,T_u+0^s_{\cdot}093104\,T_u^2-6^s_{\cdot}2\cdot 10^{-6}\,T_u^3\\[0.2cm] ~\mbox{where:}\\[0.2cm] ~~ \qquad r=1.0027379093\\ ~~ \qquad T_u=(JD_{[UT1\, date]}-2\,451\,545.0)/36\,525.0\\ \end{array} \qquad \mbox{(4)} }[/math]