If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
The SBAS Integrity Concept Standardised by ICAO: Application to EGNOS
| EGNOS | |
|---|---|
| Title | The SBAS Integrity Concept Standardised by ICAO: Application to EGNOS |
| Author(s) | Benoit Roturier, DGAC/STNA, France; Eric Chatre GSA, GNSS Supervisory Authority, Brussels, Belgium and Javier Ventura-Traveset, ESA, European Space Agency. |
| Level | Intermediate |
| Year of Publication | 2006 |
__APPROVEDREVS__
Abstract
There have been a lot of debates, within the International Civil Aviation Organisation (ICAO) GNSS Panel (GNSSP) group of experts[footnotes 1], on the proper way to ensure SBAS user safety while at the same time respecting the high availability requirement. The group finally validated a method at the GNSSP Seattle meeting in June 2000 which is reproduced in the GNSS Standards And Recommended Practices (SARPs), published in November 2002[1]. Although the technical relevant information for a SBAS system designer to implement the SBAS integrity concept is fully described in the SARPs, only the strict necessary information is reported there, and it is quite difficult to a non specialist to properly understand this important concept. Since the SBAS integrity concept is quite specific and new, some kind of complementary information to the SARPs was felt desirable. This is the main motivation of this paper, which will also illustrate how the integrity is being managed through the European EGNOS SBAS project.
Introduction
The integrity service of ICAO compliant GNSS systems may currently be provided by the three normalised augmentations known under the terms ABAS (Airborne Based Augmentation System), GBAS (Ground Based Augmentation System) and SBAS (Satellite Based Augmentation System)[1]. ABAS integrity concept relies on the single observation through the airborne user receiver of redundant pseudo range information, while GBAS (resp. SBAS) integrity elaboration relies on the use of a single (resp. a network) of ground reference stations.
In addition to integrity service, GBAS and SBAS also provide to the user differential corrections to improve the precision in a restricted area around a single reference station for GBAS and over a wide area defined by a network of reference stations for SBAS. Finally, the SBAS geo satellites also transmit a ranging navigation signal similar to a GPS satellite.
Therefore, the SBAS integrity service which is addressed here should protect the user from both:
- failures of GNSS/GEO satellites (drifting or biased pseudo ranges) by detecting and excluding faulty satellites through the measurement of GPS signals with the network of reference ground stations;
- transmission of erroneous or inaccurate differential corrections. These erroneous corrections may in turn be induced from either:
- undetected failures in the ground segment;
- processing of reference data corrupted by the noise induced by the measurement and algorithmic process.
This last type of failure, which may occur when the system is in a nominal state (no GNSS/GEO satellite failure, no ground segment/user equipment failure) is usually known as “fault free case”. Protection of the user against noise effects has been quite demanding during the process of definition and validation of the ICAO SBAS integrity concept. In fact, the potential for such non integrity events generated in fault free conditions is inherent to data measurement and processing, to provide users with basic and precise correction messages and is thus a permanent risk which has to be carefully managed. This has involved the definition of statistical error bounds called horizontal or vertical protection levels (HPL or VPL) which will be discussed in depth in section V.
Before dwelling in depth into the details of the elaboration of adequate parameters to protect users from non integrity events which might occur from system failure (section IV) or noise (section V), we will recall integrity requirements (section II) and integrity definitions (section 3).
Integrity Requirements
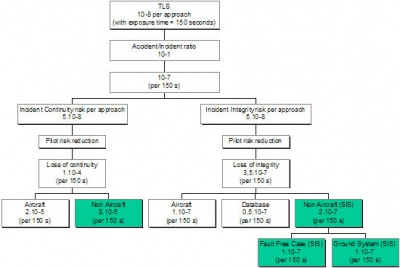
The elaboration of a high level fault tree for all phases of flight leading to a given objective in term of Target Level of Safety (TLS)[footnotes 2] and further decomposition for a number of phases of flight into aircraft, airborne database and signal in space (SIS) contribution to this risk has been provided by the ICAO All Weather Operational Panel[2] (AWOP)[3].
The fault tree for approach with vertical guidance (APVI,II and Category 1 approach type) corresponding to the most demanding operations supported by SBAS derived from AWOP work is shown in Fig. 1[footnotes 3]. This paper will focus on Non Aircraft, signal in space (SIS) integrity risk corresponding to the bottom right part allocations of Fig. 1. AWOP work has been used as input by GNSSP to define the high level integrity requirements summarised in Fig. 2.
| Typical operation | Time to Alarm | Integrity | Hor. alert limit | Vert. alert limit |
|---|---|---|---|---|
| En-route | 5 mn | 1-10-7/h | 4 NM | N/A |
| En-route | 15 s | 1-10-7/h | 2 NM | N/A |
| En-route, Terminal | 15 s | 1-10-7/h | 1 NM | N/A |
| NPA | 10 s | 1-10-7/h | 0.3 NM | N/A |
| APV I | 10 s | 1-2x10-7/app | 40.0 m | 50 m |
| APV II | 6 s | 1-2x10-7/app | 40.0 m | 20 m |
| CAT I | 6 s | 1-2x10-7/app | 40.0 m | 15 - 10 m |
Integrity Definitions
The provisions for integrity in the SARPs are complex for a non expert, but also are the definitions of non integrity events and three levels of definitions may be identified which are further discussed in this section.
High level definition of integrity
The high level definition of integrity in the SARPs is (§A.1[1]): A measure of the trust which can be placed in the correctness of the information supplied by the total system. Integrity includes the ability of a system to provide timely and valid warnings to the user (alerts).
It has to be noted that the integrity requirement in Fig. 2 includes both an alert limit in horizontal and vertical dimensions and an allocated time to warn the user. Moreover, the integrity is often specified by its inverse, integrity risk, as in Fig. 1. The integrity risk may be defined as the probability of providing a signal that is out of tolerance without warning the user in a given period of time.
The out of tolerance condition is defined in the SARPs in the user position domain. Although it might seem obvious from the high level definition of integrity given above that a non integrity event corresponds to the situation obtained when any user navigation system error (NSE) in horizontal or vertical dimensions is superior to Horizontal or Vertical Alert Limit (HAL or VAL), while not providing timely and valid warnings to the user, the definition which has been retained in the SARPs is a little bit more conservative (as shown in[4] [4]), and is described in the next section.
Non integrity event definition applicable to the ground system designer
This definition (in the most demanding case of APVII or Cat I) may be found in §B.3.5.7.5.1[1]: “Given any valid combination of active data, the probability of an out-of-tolerance condition for longer than 5.2 consecutive seconds shall be less than 2 x 10-7 during any approach, assuming a user with zero latency. An out-of-tolerance condition is defined as a horizontal error exceeding the HPLSBAS or a vertical error exceeding the VPLSBAS (as defined in B.3.5.5.6).” The Horizontal and Vertical Protection Level (HPL and VPL) are elaborated within the user receiver (cf B.3.5.5.6[1]) at each epoch by combining ground transmitted parameters, aircraft parameters and geometry of the user with respect to satellites used in the position calculation. They will be further discussed in section V. This definition (NSE > HPL or VPL) is often referenced as “Misleading Information (MI)” case. It has to be used by a SBAS system designer to prove by simulation and/or tests that the SBAS design is SARPs compliant with respect to integrity requirements. It is also a high level requirement for the calculation of ground parameters used in XPL elaboration by a SBAS system designer, as further discussed in section V.3. However, since this definition implies the knowledge of the NSE, a standard user may obviously not apply this out of tolerance test to raise a flag in case of non-integrity event.
Non integrity event definition applicable to a SBAS standard user
The test to be done at user level to check the correctness of transmitted data is defined in SARPs (§B.3.5.8.4.2[1]): “The receiver shall compute and apply horizontal and vertical protection levels defined in B.3.5.5.6” This definition is not really explicit (!), but more may be found in the guidance material section (§C.6.4.4[1]): “… If the computed HPL exceed the Horizontal Alert Limit (HAL) for a particular operation, SBAS integrity is not adequate to support that operation. The same is true for precision approach and APV operations, if the VPL exceeds the vertical alert limit (VAL).” This test (HPL or VPL > HAL or VAL), which is implemented at each epoch, allows to declare the SBAS “system unavailable” for a given level of operation since in this case the probability of an MI (and HMI) event is high. Note that xPL and xAL (x stands either H or V) are now known by the user. If a SBAS is SARPs compliant as defined in section II.2, then a user applying the above test will be protected to the required level.
Example
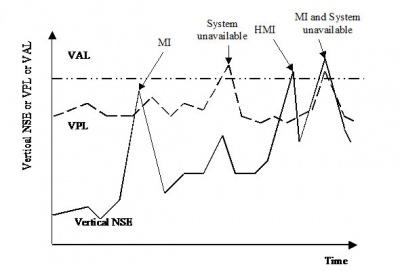
The three above discussed integrity tests (HMI, MI and system unavailable) appear more explicitly in figure 3:
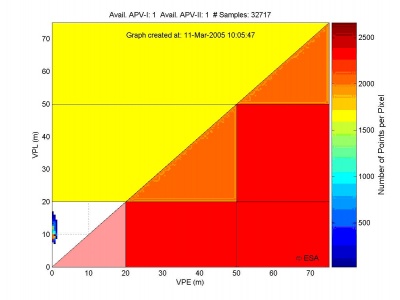
Another practical representation of these different cases is obtained through a 2D plot of the Vertical Position Error (VPE) against the VPL where each pixel corresponds to a measurement epoch as in Fig. 4. This is usually known in Europe as the Stanford diagram. Fig. 4 illustrates the trade off between integrity and availability (Stanford diagram) as obtained through EGNOS real measurements at the ESA EGNOS P.O. in Toulouse, France on March 2005. The diagonal traces the limit between the safe operation of the system (left side) and the unsafe conditions (right side). The EGNOS System is shown to be safe in the nominal test conditions of Fig. 4, with an availability of both APV-1 and APV-1 of 100% for this specific test period.
When focusing on integrity, an interesting modification of the all in view Stanford diagram is the Stanford-ESA Integrity diagram, where for a specific user location and period interval, every computed sample represents the worst possible geometrical integrity situation for that user at that location. Thus, if no integrity risk violation is observed with the Stanford-ESA Integrity diagram computation at a given location and for a given period of time, we may certainly conclude that for all possible GPS satellite geometries and SBAS information that could potentially be used in that location and for that period, the system was safe (please refer to The Stanford – ESA Integrity Diagram: Focusing on SBAS Integrity for more details).
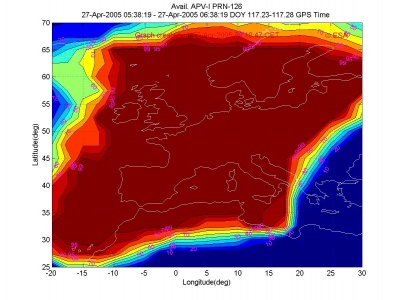
Fig. 5, obtained trough the ESA EGNOS performance real time website shows typical EGNOS coverage across Europe of APV-I (VAL=50 metres). It is to be noted that during this measurement campaign two EGNOS reference stations in South/East of Europe were not yet deployed, which explains the outage in that area.
Ground System Integrity
The ground system integrity risk allocation shown at the bottom of Fig. 1 (10-7/app in case of APV and Cat I operations) should cover:
- Failures on navigation code and data transmitted by GNSS satellites (including evil waveforms).
- Corruption of data to be transmitted to the user, through the geo satellites.
- Failures issued from the ground system hardware, software design or corruption of data through the Wide Area Network connecting the ground elements.
Faulty GNSS satellites
When such a failure occurs, the ground segment will provide the appropriate corrections along with the parameters allowing XPL calculation, unless the error gets too large in which case the faulty satellite is flagged with a ”don’t use” status. When the error is not significantly large, the user equipment will process these data and the only impact will be on system availability and continuity through XPL inflation at user level. In EGNOS system, specific modulation distortion failures (evil waveforms) are also managed through Signal Quality Monitoring (SQM) defined in ICAO Amendment 77[1] using specific Reference and Integrity Monitoring Stations type C (RIMS C).
Corruption of data through geo link
EGNOS has implemented the following techniques defined in ICAO SARPs[1] to minimise at the lowest possible level the risk of data corruption through the geo link:
- convolutional encoding adding a bit to each information bit, allowing Forward Error Correction (FEC) at the receiver level and providing a high level of robustness to channel burst errors.
- 24 bit Cyclic redundancy check (CRC) providing a very low probability of undetected error within a message.
Bit to bit comparison of transmitted messages in the ground segment is also realised. The impact of errors induced by this type of failures at user level should therefore be very low.
Hardware, Software and Wide Area Network failure
No recommendation exists in the SARPs on the design of the ground segment. The SBAS system designer has to demonstrate that the probability of undetected failures transmitted through the SIS will be inferior to the integrity risk allocation for ground system failures given in Fig. 1. Due to space restriction, it is not possible to go into details in this paper of ESA recommended techniques to provide the required integrity level for EGNOS. Some important features are listed below:
- Two independent processing chains, one checking the other, fed by two different reference stations (RIMS A and B) developed by separate manufacturers to avoid common modes of failure are implemented
- Specific and independent RIMS –C network for evil waveform detection
- Software integrity is managed through appropriate design methodology (based on DO178B Standards).
- A complementary set of integrity mechanisms which are automatic safety devices (no actions of operators required as the time to alarm requirements does not allow it) and they are independent of the EGNOS monitoring & control,
- All data transported over the EGNOS Wide Area Network is protected by a 32 bit CRC.
The undetected failures from the ground segment could introduce corrupted data in the transmitted messages. If the integrity requirement is not met, the user will obviously not be protected against such failures by the XPL algorithms. To fulfil the integrity requirements, the ground system shall reduce the probability of failure of each critical function and shall be able to detect this kind of failures with a global probability of missed detection (Pmd) defined by:
[math]\displaystyle{ Pmd_{ground\,monitor} = \frac{Integrity\,requirement}{Pr failure_{ground\,segment}} }[/math]
Fault Free Case Integrity
The XPL algorithms
To protect the user against misleading information (MI) due to data corrupted by the noise induced by the measurement and algorithmic process when the system is in a nominal state (no GNSS/GEO satellite failure, no ground segment/user equipment failure), it has been shown that SARPs require the elaboration by the ground segment of two different parameters used in the XPL computation. These parameters give an indication on the error uncertainty, which is modelled by:
- the variance (σUDRE) of a zero-mean normal distribution which describes the user differential range errors (UDRE) for each ranging source after application of fast and long-term corrections, and excluding atmospheric effects and receiver errors,
- the variance (σUIRE) of a zero-mean normal distribution which describes the L1 residual user ionospheric range error (UIRE) for each ranging source after application of ionospheric corrections. This variance is determined from the variance (σGIVE) of an ionospheric model based on the broadcast grid ionospheric vertical error (GIVE)[footnotes 4].
The other potential errors to affect user integrity in nominal conditions considered by GNSSP are:
- aircraft pseudo range errors due to the combination of receiver and aircraft multipath (ground multipath is not considered here). This error is well characterised by a zero mean normal distribution whose variance σair is given by the sum of SARPs modelled variance of receiver and aircraft multipath error.
- The residual pseudo range error of a tropospheric correction model, characterised by a variance σtropo which is defined by a standard model in the SARPs
Since all these individual pseudo range errors are supposed to be characterised by independent, zero mean, normal distributions, the global residual pseudo range error for the i-th ranging source (σi) may also be characterised by a zero mean normal distribution whose variance is:
[math]\displaystyle{ {\sigma}^2_i = {\sigma}^2_{i,flt}+{\sigma}^2_{i,UIRE}+{\sigma}^2_{i,air}+{\sigma}^2_{i,tropo} }[/math] (1)
Where σi,flt may be straightforwardly derived from δUDRE through a tedious calculation given in SARPs (B.3.5.5.6.2[1]) to take into account degradation parameters in case of missed SBAS messages. From (1), and for a given user to ranging sources geometry, it is quite straightforward to derive the vertical protection level (VPL) equation by:
- going from the pseudo range variance domain through the position variance domain (this is necessary because the integrity definitions are all in the position domain)
- by scaling the position domain variance to the integrity requirement.
The first step is straightforward since it is well known that the position domain residual error can be considered as a linear combination of pseudo range errors used in the navigation solution. Therefore the variance in the position domain residual error is a linear combination of σi2 and is also representative of a zero mean Normal law:
[math]\displaystyle{ {\sigma}^2_{Vposition} = \sum_{i=1}^N S^2_{V,i}{\sigma }^2_{i} }[/math] (2)
Where SV,i are geometrical parameters defined in ICAO Amendment 77[1], RTCA-DO 229[5]. The second step is obtained by multiplication of the position domain variance by a factor K that propagates this variance to a level compatible with the integrity requirement. The VPL equation is then simply:
[math]\displaystyle{ VPL_{SBAS}=K_V{\sqrt{\sum_{i=1}^N S^2_{V,i}{\sigma }^2_{i}}} }[/math] (3)
The derivation of K, which not very explicit in the SARPs, is given in section V.2.
Derivation of K factors for XPL computations
First it is important to note that the probability of missed detection of a MI event associated to the XPL algorithm (PmdXPL) has to be expressed per sample (per each XPL computation). In order to establish the link between this Pmd and the integrity requirement, it is necessary to make assumptions on the number of independent sample per time unit. For example if there are n independent samples/operation, and the integrity requirement for this operation is 10-x, the Pmd to be specified for the XPL will be:
[math]\displaystyle{ Pmd_{XPL} = \dfrac{10-x} {n} }[/math] (4)
Therefore in order to establish the appropriate value of K, it is necessary to first determine the number of independent samples per time unit. Based on ionospheric corrections, 360 s has been adopted as a reasonable assumption to ensure independence. Using this value, it is possible to compute the required probability of missed detection associated to HPL for each phase of flight.
- En route to NPA: the requirement is 0.5.10-7/h
PmdHPL = 0.5.10-7 * 360 / 3600 ~ 5*10-9 per sample
- APV I, II, Cat I: The apportionment between HPL and VPL has been chosen such that the continuity of service is maximised. Since there is a conformable margin on the horizontal position (larger alert limit and better accuracy performance), the integrity allocation has been minimised. The following Pmd have been chosen (ICAO Amendment 77[1],RTCA-DO 229[5]) for HPL and VPL (a decorrelation time of 360s implies that during the approach (150s) there is only one independent sample):
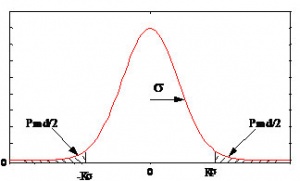
PmdHPL = 10-9 per sample., PmdVPL = 10-7 per sample Using appropriate statistical laws for the distribution of residual position errors, it is now possible to compute the K factor that scales the variance to a level compatible with the integrity requirement. K is determined from a Rayleigh distribution for En route to NPA applications since the protection has to be bi-dimensionnal. For APVI, II and Cat. I applications, two uni-dimensional k factors are determined from a Normal distribution corresponding to the lateral (crosstrack) and vertical protections. Looking at Fig. 6, it may be seen that the value of K may be directly calculated from the knowledge of the cumulative distribution function (cdf) of the relevant statistical law.
- For en route to NPA applications, the value for K is therefore:
KH NPA = Rayleigh cdf -1(1-5*10-9) = 6.18.
- For precision approach (PA) applications (APV I, II, Cat 1), the K values for lateral and vertical protections are:
KV PA = Normal cdf -1(1-10-7/2) = 5.33 KH PA = Normal cdf -1(1-10-9/2) = 6.0 These values are in accordance with the K parameters given in the SARPs in section B.3.5.5.6.1.
Discussion on zero mean, normal distribution assumption
As stated in the SARPs (§C.6.4.5[1]): “One of the most challenging tasks for an SBAS provider is to determine UDRE and GIVE variances such that the protection level integrity requirements are met without impacting availability. The performance of individual SBAS depends on the network configuration, geographical extent and density, the type and quality of measurements used and the algorithms used to process the data.” An important item in the background of this statement is that the variances representative of the ground system residual errors for each ranging sources have to be derived from zero mean Normal laws for the XPL computation to be valid. It has been shown in the previous section that this assumption is important in several steps of the XPL algorithm elaboration.
However in practice the distribution of individual pseudorange residual error, although in practice not very different from Normal laws, may not have Normal tails, or not have a zero mean, or sufficient data to demonstrate the distribution may not be available. When this issue was first investigated in the aviation community, the idea was that overbounding the individual arbitrary error distributions contributing to the position domain error by zero mean normal distributions would allow to overbound the distribution of total error with a zero mean normal distribution which could then be used in the XPL algorithm.
However further inspection revealed that this idea might not be valid for any individual error distribution. It was shown[6] that a sufficient condition for the above overbounding strategy to hold was that each initial error distribution was not necessarily normal but unimodal and symmetric. Still, it was not possible to ensure that for any SBAS this condition would be true, since the ground segment architecture is not specified in the SARPs.
ICAO GNSSP then finally decided at Seattle meeting in June 2000 that since the shape of the error distributions will be very dependant of the SBAS system architecture and algorithms and no general overbounding method could be identified, it would be the responsibility of the system designer to provide a method to compute UDRE and GIVE variances in compliance with the high level 2.10-7/app requirement given in section 3.2. Two detailed work plans (called Integrity & Continuity work plans) have been launched in the case of EGNOS, specifically, to assess that methodology in detail for the case of EGNOS own architecture and algorithms.
Summary
The ICAO validated SBAS integrity concept which will be published in SARPs in November 2001 has been summarised in this paper and some examples issued from ESA current design of EGNOS have tried to illustrate how it may be practically implemented. This paper has tried to highlight the following items:
- integrity allocation between the different potential error contributors;
- difference between the integrity definitions existing in the SARPs and their domain of application;
- XPL concept to protect the user in nominal (fault free) conditions;
- final recommendation of GNSSP on the derivation of ground parameters used in XPL calculation.
The concepts presented in this paper are all described in the SARPs but they may be disseminated through several sections and also since the SARPs have to be as compact as possible, the rationale for particular choice of parameters or methods is usually not explicit in the SARPs. It is the authors wish then that this paper might have contributed to bridge the gap from the SARPs formal requirements to a more complete vision of SBAS integrity issues.
Notes
- ^ Currently (2006) known as Navigation System Panel (NSP).
- ^ The top TLS objective is that the probability of accident leading to hull loss should be inferior to 1.5 10-7 per flight.
- ^ The AWOP 2.10-7 figure for SIS integrity risk by approach (150 s) has been further decomposed by GNSSP into a 10-7/approach allocation for the ground system integrity risk and a 10-7/approach allocation for the fault free case.
- ^ More precise definitions of the ground segment elaborated parameters σUDRE and σGIVE may be found in ICAO Amendment 77, §C.6.4.6 and C.6.4.7.
References
- ^ a b c d e f g h i j k l m ICAO Amendment 77, Annex 10 to the Convention on International Civil Aviation, Aeronautical Telecommunications: International Standards and Recommended Practices, Volume 1, Radio Navigation Aids, November 2002.
- ^ ICAO AWOP/15 Report, 15th meeting, Montreal 26 September- 12 October 1994.
- ^ ICAO AWOP/16 Report, 16th meeting, Montreal 23 June- 4 July 1997.
- ^ Liu Fan, “Analysis of Integrity Monitoring for The Local Area Augmentation System Using The GNSS”, PhD. Report, Ohio University, August 1998.
- ^ a b RTCA, “Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment”, RTCA-DO 229 C, November 2001.
- ^ Bruce DeCleene, “Defining Pseudo Range Integrity – Overbounding” ION Conference, September 2000.