If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Solar Time
| Fundamentals | |
|---|---|
| Title | Solar Time |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
The Solar Time is affected by two main causes:
- The orbit of the earth is elliptic, thus, according to the second Kepler's law [footnotes 1] the orbital speed is not constant.
- The Earth's axis of rotation is not perpendicular to the plane of earth's orbit around sun [footnotes 2] and, thence, the angular rate is not constant [footnotes 3]. It moves fastest at the end of December and slowest at mid-September.
To have a more uniform time, a fictitious Mean Sun is defined, which moves along the (celestial) equator of earth with uniform speed (mean velocity of the actual sun). Using this mean sun, one defines Mean Solar Time as the hour angle [footnotes 4] of the centre of the mean sun.
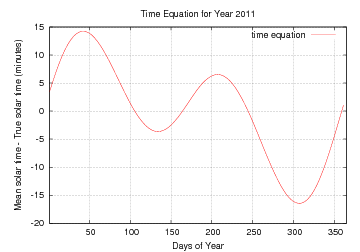
The difference between Mean Solar Time and True Solar Time is reflected in the Equation of Time, which is a periodic function with a one year period. Figure 1 shows a plot of the Equation of Time. This evolution is the direct consequence of the two effects on the apparent Solar rotation rate described above.
From Mean Solar Time, Civil Time is defined as Mean Solar Time augmented in 12 hours, so that each day begin at midnight [footnotes 5]. Civil Time is local, i.e., associated to local meridians. In order to have a global time not linked to these local meridians, Universal Time (UT) is defined as the Civil Time at Greenwich meridian.
On the other hand, the earth's rotation rate is not uniform. It is affected by secular variations, mainly due to the tidal frictions, seasonal changes and other irregular
or like random effects, producing variations in the earth's mass distribution and moment of inertia. To deal which such effects, the following times (or refinements of UT) have been introduced:
- UT0: is the mean solar time at the Greenwich meridian and is determined at a particular observatory by astronomic observations. As this time is based on the instantaneous earth rotation, thence it is affected by both earth's irregular spin rate and polar motion.
- UT1: is obtained by correcting UT0 for the effect of polar motion on the observing site location (i.e., deducting to the CTP pole, see Transformations between Time Systems):
- [math]\displaystyle{ UT1=UT0+\Delta l \qquad \mbox{(1)} }[/math]
- where:
- [math]\displaystyle{ \Delta l=\frac{1^{s}}{15}\;(x_p\; \sin \lambda -y_p\; \cos \lambda)\; \tan \varphi \qquad \mbox{(2)} }[/math]
- UT1 is the same around the world (i.e., it does not depend on the observatory location). This time is fundamental in geodetic astronomy, because it defines the orientation of the conventional terrestrial system (see articles Reference Systems and Frames and Conventional Terrestrial Reference System) in space.
- UT2: is obtained by removing periodic seasonal variations in UT1 time (see Transformations between Time Systems), but it is not uniform enough due to other effects on the earth's rotation still remaining. Nowadays it is considered obsolete.
- [math]\displaystyle{ UT2=UT1+\Delta S \qquad \mbox{(3)} }[/math]
Notes
- ^ The radius vector from the sun to the earth sweeps out equal areas in equal times.
- ^ The sun moves around the ecliptic not the equator. The ecliptic is the apparent circular path of the sun on the celestial sphere during the course of a year. The plane of the ecliptic is inclined an angle of about 23[math]\displaystyle{ ^{o} }[/math]26[math]\displaystyle{ ^' }[/math] with respect to the equator, see equation (5) in ICRF to CEP.
- ^ The angular displacement of sun measured over the ecliptic and over the equator are not linearly related.
- ^ Sun hour angle: is the angular displacement of the sun (measured over the equator and in retrograde sense) from the local meridian. Thence, it is zero when the sun is on the local meridian (solar noon), negative before local noon and positive in the afternoon.
- ^ Midnight is the time when the hour angle of Mean sun's centre is at a longitude of [math]\displaystyle{ 180^o }[/math].