If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Satellite Eclipses
| Fundamentals | |
|---|---|
| Title | Satellite Eclipses |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
High-precision GNSS positioning degrades during the GNSS satellites eclipse seasons. Indeed, once the satellite goes into the shadow, the radiation pressure vanishes. This effect introduces errors in the satellite dynamics due to the difficulty to properly modelling the solar radiation pressure. On the other hand, the satellite solar sensors lose sight of the sun and the attitude control (trying to keep the panels facing the sun) is degraded. The yaw attitude of GPS satellites is essentially random during an eclipse and for up to [math]\displaystyle{ 30 }[/math] minutes past exiting from shadow [1].Each GPS satellite has two eclipse seasons per year, each lasting for about seven weeks [2].
As a consequence, the orbit during shadow and eclipse periods may be considerably degraded and the removal of satellites under such conditions can improve the high-precision positioning results.
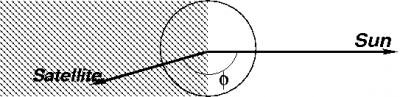
The eclipse condition can be defined from a simple cylinder model for the shadow of the Earth (see figure 1) [2]
- [math]\displaystyle{ \cos \phi =\displaystyle \frac{{\mathbf r}^{sat}\cdot {\mathbf r}_{sun}}{ {r}^{sat} {r}_{sun}} \lt 0 }[/math] and [math]\displaystyle{ r^{sat} \sqrt{1-\cos^2 \phi}\, \lt a_e \qquad \mbox{(1)} }[/math]
Where [math]\displaystyle{ {\mathbf r}^{sat} }[/math] and [math]\displaystyle{ \displaystyle r^{sat} }[/math] are the vector from the geocentre to the satellite and the magnitude of that vector, respectively. Vector [math]\displaystyle{ {\mathbf r}_{sun} }[/math] is the geocentre vector to sun and [math]\displaystyle{ \displaystyle {r}_{sun} }[/math] is its magnitude, while [math]\displaystyle{ \displaystyle a_e }[/math] is the mean equatorial radius of the Earth (see table (1) or (2) in Reference Frames in GNSS).
Notice that, as commented before, the satellites should be removed during the eclipse condition and also during the first [math]\displaystyle{ 30 }[/math] minutes, at least, after exiting from eclipse.
References
- ^ [Bar-Sever, Y.E., 1994] Bar-Sever, Y.E., 1994. Improvement to the GPS attitude control subsystem enables predictable attitude during eclipse seasons.
- ^ a b [Mervat, 1995] Mervat, L., 1995. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System. PhD. University of Bern, Philosophisch-naturwissenschftichen Fakultat.