If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Relativistic Path Range Effect: Difference between revisions
mNo edit summary |
Gema.Cueto (talk | contribs) No edit summary |
||
| Line 15: | Line 15: | ||
where <math>\displaystyle r^{sat}, r_{rcv} </math> are the geocentric distances of satellite and receiver and <math>\displaystyle r_{rcv}^{sat} </math> is the distance between them. The constants <math>\displaystyle c = 299792458 | where <math>\displaystyle r^{sat}, r_{rcv} </math> are the geocentric distances of satellite and receiver and <math>\displaystyle r_{rcv}^{sat} </math> is the distance between them. The constants <math>\displaystyle c = 299792458 m/s </math> and <math>\displaystyle \mu=G\,M_\oplus=3.986004418 \cdot 10^{14}\, m^3/s^2 </math> are the speed of light and the Earth's gravitational constant, respectively (see [[Reference Frames in GNSS]]). | ||
Latest revision as of 14:00, 2 June 2022
| Fundamentals | |
|---|---|
| Title | Relativistic Path Range Effect |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
This is a secondary relativistic effect that can be required only for high accuracy positioning. Its net effect on range is less than 2 cm and thence, for most purposes it can be neglected.
This effect is named the Shapiro signal propagation delay and introduces a general relativistic correction to the geometric range: Due to the space-time curvature produced by the gravitational field, the Euclidean range, computed by equation (3) in article Code Based Positioning (SPS), must be corrected by an amount given by the expression:
- [math]\displaystyle{ \Delta \rho_{_{rel}}=\frac{2\,\mu}{c^2}ln\frac{r^{sat}+r_{rcv}+r_{rcv}^{sat}}{r^{sat}+r_{rcv}-r_{rcv}^{sat}} \qquad \mbox{(1)} }[/math]
where [math]\displaystyle{ \displaystyle r^{sat}, r_{rcv} }[/math] are the geocentric distances of satellite and receiver and [math]\displaystyle{ \displaystyle r_{rcv}^{sat} }[/math] is the distance between them. The constants [math]\displaystyle{ \displaystyle c = 299792458 m/s }[/math] and [math]\displaystyle{ \displaystyle \mu=G\,M_\oplus=3.986004418 \cdot 10^{14}\, m^3/s^2 }[/math] are the speed of light and the Earth's gravitational constant, respectively (see Reference Frames in GNSS).
This correction must be added to the Euclidian distance given by the following equation (2).
- [math]\displaystyle{ \rho_{rcv}^{sat}=\left\|{\mathbf r}^{sat}-{\mathbf r}_{rcv}\right \|=\sqrt{(x^{sat}-x_{rcv})^2+(y^{sat}-y_{rcv})^2+(z^{sat}-z_{rcv})^2} \qquad \mbox{(1)} }[/math]
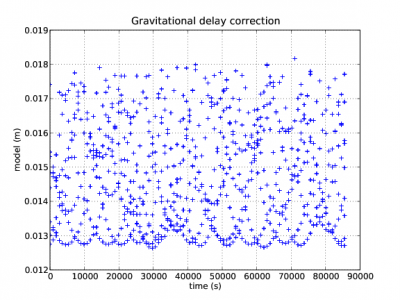
Next figure 1 illustrates with an example the Shapiro signal propagation delays for the satellites in view from a receiver in Barcelona, Spain (receiver coordinates [math]\displaystyle{ \lambda\simeq 2^ o }[/math] [math]\displaystyle{ \phi \simeq 41^o }[/math]).
A very good review of relativistic effects on GPS can be found in [Ashby, N., 2003] [1] , (see https://link.springer.com/content/pdf/10.12942%2Flrr-2003-1.pdf).
References
- ^ [Ashby, N., 2003] Ashby, N., 2003. Relativity in the Global Positioning System