If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Receiver Antenna Phase Centre
| Fundamentals | |
|---|---|
| Title | Receiver Antenna Phase Centre |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
The measurements are referred to the Antenna Phase Centre (APC) position. As this location is frequency dependent, a point tied to the base of the antenna is used as a more suitable reference. This point is named Antenna Reference Point (ARP). The manufacturers provide technical information on the APC position relative to the ARP. On the other hand, relative and absolute antenna phase centre corrections have been compiled by IGS and are provided in the PCV and ANTEX files respectively for several antenna models (see Antenna Phase Centre).
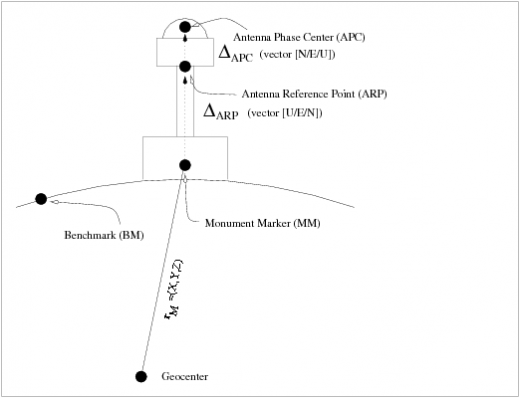
In geodetic positioning, the receiver coordinates are referred to a Monument Marker (MM) or to an external Benchmark (BM). Figure 1 illustrates this concept.
In the IGS SINEX files, the computed coordinates for Monument Marker coordinates are given in the block "SOLUTION/ESTIMATE", in ECEF coordinates, for each processed station. The position of the ARP relative to the MM, or the site eccentricity vector, are given the block "SITE/ECCENTRICITY" in Up North East (UNE) coordinates. Finally, the Antenna Phase Centre offsets for the different frequencies used and the Antenna Calibration model (e.g., ANTEX file) are given in the "SITE/GPS_PHASE_CENTER" block of data [footnotes 1].
Let [math]\displaystyle{ {\mathbf r}_{M} }[/math] be the position of Monument Marker in a ECEF reference frame. Let [math]\displaystyle{ {\boldsymbol \Delta}_{ARP} }[/math] be the offset vector defining the ARP position relative to the Monument Marker, and [math]\displaystyle{ {\boldsymbol \Delta}_{APC} }[/math] the offset vector defining the APC position relative to the ARP. Thence the receiver APC position [math]\displaystyle{ {\mathbf r} }[/math], in a ECEF reference frame is given by [footnotes 2]:
- [math]\displaystyle{ {\mathbf r}={\mathbf r}_M+{\boldsymbol \Delta}_{ARP}+{\boldsymbol \Delta}_{APC} \qquad\mbox{(1)} }[/math]
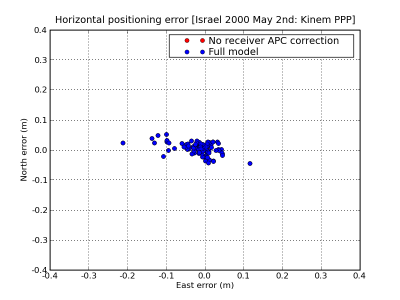
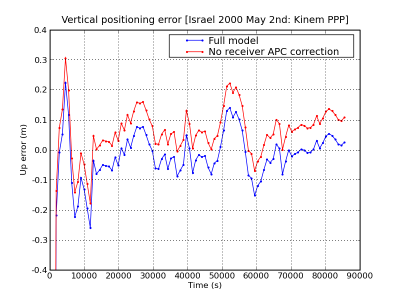
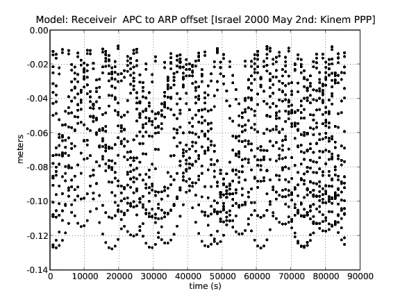
Figure 2: Receiver Antenna Phase Centre: Range and position domain effect. First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the Receiver APC correction. The variation in range is shown in the second row at left. As the APC vector is along the vertical axis, its effect is a displacement in the vertical component
Figure 2, shows an example illustrating the effect of APC correction in the positioning domain (first row) and range domain (second row). The solution computed using the APC correction is shown in blue and the solution without using the APC in red. The projection in range of the APC offset is shown in the second row at left. The results correspond to an Ashtech-ZXII3 receiver with ASH70093D_M antenna, located at coordinates [math]\displaystyle{ \lambda=34^o45^m }[/math], [math]\displaystyle{ \phi=30^o36^m }[/math] (Israel), on May 2nd 2000 and positioned in Kinematic Precise Point Positioning (PPP) mode.
Notes
- ^ See SINEX format at: http://www.iers.org/MainDisp.csl?pid=190-1100110. SINEX files can be found at ftp://cddis.gsfc.nasa.gov/pub/gps/products.
- ^ Note: As commented before, [math]\displaystyle{ {\boldsymbol \Delta}_{APC} }[/math] is a frequency dependent correction. Equation
- [math]\displaystyle{ {\boldsymbol \Delta}_{APC_{LC}}=\frac{f_1^2 {\boldsymbol \Delta}_{APC_{L1}}-f_2^2 {\boldsymbol \Delta}_{APC_{L2}}}{f_1^2-f_2^2} }[/math]