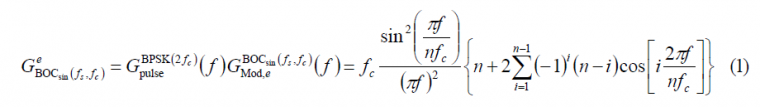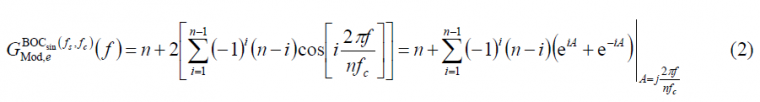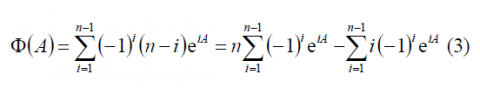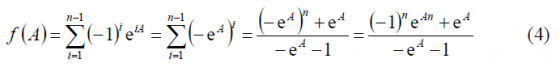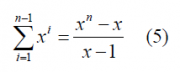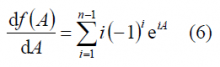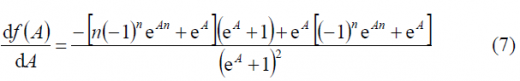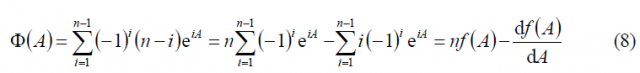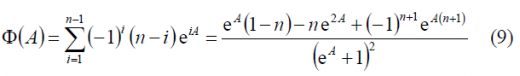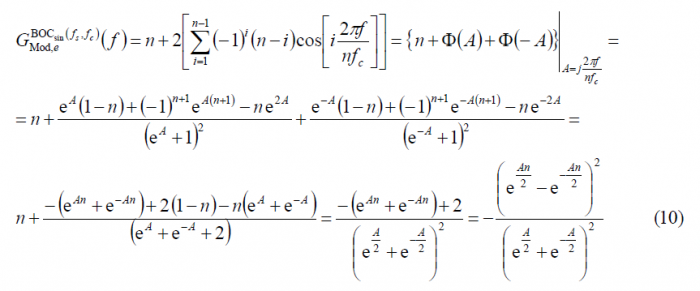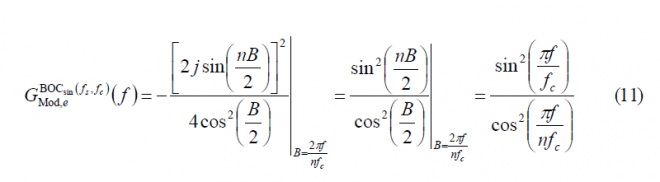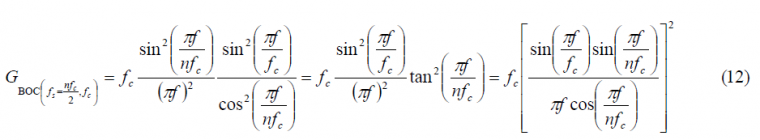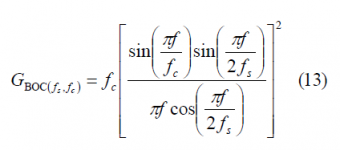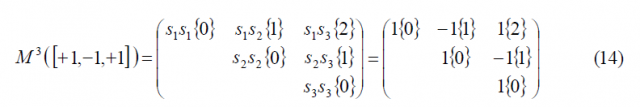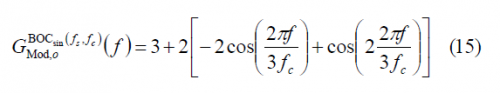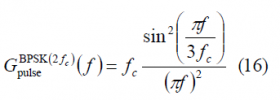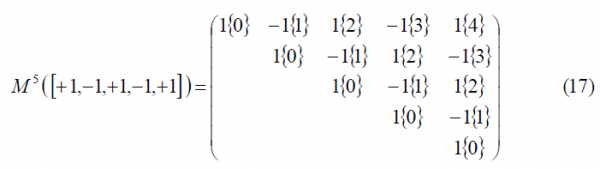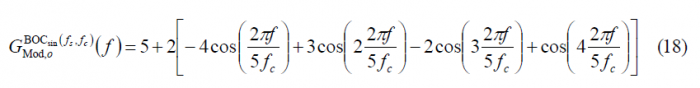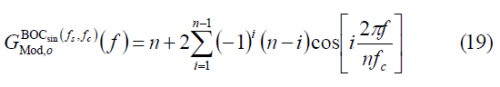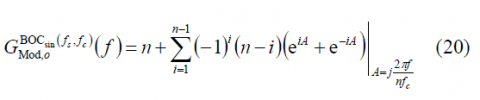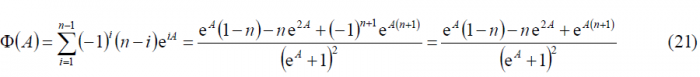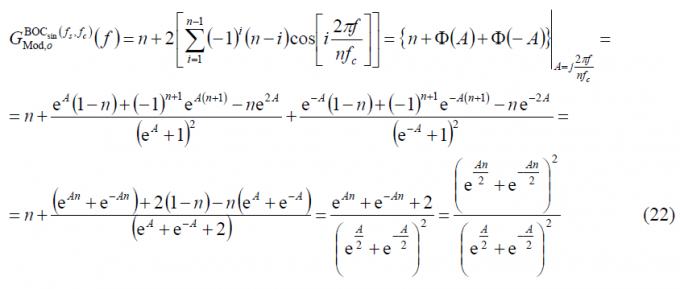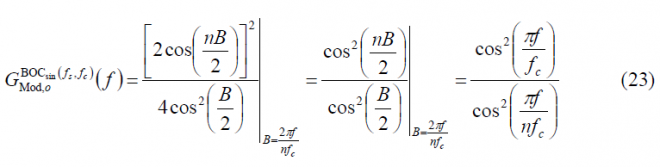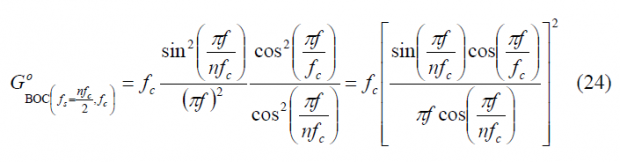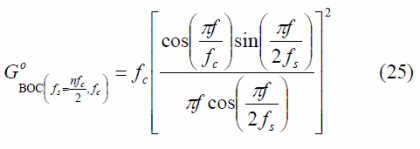If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Power Spectral Density of Sine-phased BOC signals
| Fundamentals | |
|---|---|
| Title | Power Spectral Density of Sine-phased BOC signals |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
The power spectral density of any BOC[math]\displaystyle{ \left(f_s,f_c\right) }[/math] in sine phasing can be expressed using the theory on Multilevel Coded Spreading Symbols (MCS) signals as follows:
(B.1) where the superindex e indicates the even case. Moreover, the modulating factor for the even case presents the following form:
(B.2)
As we can see, the problem to calculate can be reduced into an easier one by means of the following auxiliary function [math]\displaystyle{ \Phi \left(A\right) }[/math]:
and also with the auxiliary function , defined as follows:
where we have made the change
The interesting property about the above defined function is shown in the next relationship:
In fact, taking (4)we can see that
Thus (3) can be rewritten as follows
Combining now (4) and (6) according to (8) we obtain the following expression:
And the modulating function simplifies thus to:
where we have also taken into account that according to the definition of the BOC modulation in terms of a BCS vector, n is even in the even version. Additionally, since A can also be expressed as A=jB the expression above simplifies to
Once a simplified form has been derived for the BCS modulating factor of BOC(fs, fc), we substitute in (1) yielding the well-known expression for the Power Spectral Density (see Binary Offset Carrier (BOC)):
Since , the equation (12) can also be expressed as follows:
This is the well known expression that we find everywhere in the literature. Now that we have solved the case of the even BOC modulation in sine phasing, we calculate next its odd counterpart. For the case of the odd BOC modulation in sine phasing, we have to derive first a general expression for any odd n. We will proceed by generalizing over n.
For n = 3, [math]\displaystyle{ BOC_{sin}\left(f_s,f_c\right) }[/math] can also be expressed as BCS([+1,-1,+1], fc), such that the generation matrix will adopt the following form:
Thus, the odd modulating term yields this time:
where o indicates the odd case, and
In the same manner, for , [math]\displaystyle{ BOC_{sin}\left(f_s,f_c\right)=BOC_{sin}\left(2f_c,f_c\right) }[/math] what can also be defined as in the general form BCS([+1,-1,+1,-1,+1], fc) with generation matrix given by:
Thus, for the case of , we will have:
If we continue by induction we can find the expression for any odd n:
As we can recognize, (19) is equal to (2) except that n is odd now with [math]\displaystyle{ n \in \left \{ 3,5,7,\cdots \right \} }[/math] Moreover, it can be shown that for the odd [math]\displaystyle{ n=2f_s/f_c }[/math] is still valid. For simplicity, we express the modulating factor above using its exponential equivalent expression:
Using now the expressions derived above for the sum term [math]\displaystyle{ \Phi\left(A\right) }[/math], it can be shown that:
Again, this expression is similar to that obtained for the even case, but with a slight difference. Indeed, since n is odd, the second summand in the numerator has a changed sign with respect to (9). The modulating function is thus shown to present the following form:
Additionally, since A can also be expressed as A=jB, (22) simplifies to
Once we have the BCS modulating factor of an arbitrary odd [math]\displaystyle{ BOC\left(f_s,f_c\right) }[/math] it can be shown that the power spectral density is (see Binary Offset Carrier (BOC)):
which coincides perfectly with the expressions found in the literature [J. W. Betz, 1999][1], [A.R. Pratt and J.I.R. Owen, 2003][2] and [E. Rebeyrol et al., 2005][3].
Furthermore, since [math]\displaystyle{ n=2f_s/f_c }[/math], the previous expression can also be shown as follows:
References
- ^ [J. W. Betz, 1999] J. W. Betz, The offset carrier modulation for GPS modernization, in Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 1999, pp. 639–648, January 1999, San Diego, California, USA.
- ^ [A.R. Pratt and J.I.R. Owen, 2003] Anthony R. Pratt & John I.R. Owen, BOC Modulations Waveform, Proceedings of the International Technical Meeting of the Institute of Navigation, ION-GNSS 2003, 9-12 September 2003, Portland, Oregon, USA.
- ^ [E. Rebeyrol et al., 2005] E. Rebeyrol, C. Macabiau, L. Lestarquit, L. Ries, J-L. Issler, M.L. Boucheret, M. Bousquet , BOC Power Spectrum Densities, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 2005, 24-26 January 2005, Long Beach, California, USA.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)