If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Examples of single frequency Cycle-Slip Detectors
| Fundamentals | |
|---|---|
| Title | Examples of single frequency Cycle-Slip Detectors |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
The examples of single frequency detectors presented next are based only on data measurements of a single receiver and does not use any geometrical delay model. They are simple algorithms, suitable to run in real-time, but with worse performance that the two frequency detectors of previous sections. Other algorithms using geometrical modelling or single or double differences between satellites, or satellites and receivers, can improve the detection threshold and the reliability.
The non dispersive delays (geometry, clocks, troposphere ...) are cancelled when forming the code-pseudorange and carrier-phase combination for a given satellite and receiver measurement (i.e., [math]\displaystyle{ \Phi-R=\lambda N -2 I+K+\varepsilon }[/math]) being the ionospheric refraction [math]\displaystyle{ I }[/math] affected by a factor two. The terms [math]\displaystyle{ N }[/math], [math]\displaystyle{ K }[/math] and [math]\displaystyle{ \varepsilon }[/math] indicate the ambiguity, instrumental delays and measurement noise.
Two examples of algorithms are presented based in the following considerations:
- The ionospheric term [math]\displaystyle{ I^s_r }[/math] varies slowly with time, with small changes between consecutive epochs (typically less than [math]\displaystyle{ 1-2 }[/math] centimetres in [math]\displaystyle{ 30 }[/math] seconds).
- The measurement noise [math]\displaystyle{ \varepsilon }[/math] can reach up to several cycles, but it can be smoothed by a polynomial fit of the data measurements over a moving window (example 1), or a smoothed prediction can be computed by averaging the samples (example 2).
Algorithm description: Example 1
The detection is based on fitting a [math]\displaystyle{ n }[/math]-degree polynomial over a sliding window of [math]\displaystyle{ N }[/math] samples (e.g., [math]\displaystyle{ N=200 }[/math] with 1Hz data). The residuals (predicted-observed) are compared to identify the carrier phase cycle-slips [footnotes 1]. As the geometry-free combination is affected by the ionospheric refraction, a sampling rate dependent threshold can also be considered.
- Input data: Code minus phase combination of a single frequency data.
- [math]\displaystyle{ d(s;k)=\Phi(s;k)-R(s;k) \qquad \mbox{(1)} }[/math]
- Output: satellite (PRN), time, cycle-slip flag
- For each epoch ([math]\displaystyle{ k }[/math])
- For each tracked satellite ([math]\displaystyle{ s }[/math])
- Declare cycle-slip when data hole greater than [math]\displaystyle{ tol_{\Delta t} }[/math] [footnotes 2].
- If no data hole larger than [math]\displaystyle{ tol_{\Delta t} }[/math], thence:
- Update an array with the previous [math]\displaystyle{ N }[/math] values (after the last cycle-slip) [math]\displaystyle{ [d(s;k-N),\dots,d(s;k-1)] }[/math]
- Fit a n-degree polynomial [math]\displaystyle{ P(s;x) }[/math] to the previous values [footnotes 3].
- Declare cycle-slip when:
- [math]\displaystyle{ \begin{array}{l}
\left |d(s;k) -P(s;k) \right |\gt Threshold
\end{array}
}[/math]
- Reset algorithm after cycle slip.
- End
- For each tracked satellite ([math]\displaystyle{ s }[/math])
- End
- For each epoch ([math]\displaystyle{ k }[/math])
Algorithm description: Example 2
The detection is based on computing the mean and sigma values of the code pseudorange and carrier phase ([math]\displaystyle{ \Phi-R }[/math]) differences over a sliding window of [math]\displaystyle{ N }[/math] samples (e.g., [math]\displaystyle{ N=100 }[/math] with 1Hz data). A cycle-slip is declared when a measurement differs from the mean bias value over a predefined threshold.
: Input data: Code pseudorange ([math]\displaystyle{ R }[/math]) and carrier phase ([math]\displaystyle{ \Phi }[/math]) measurements.
: Output: satellite (PRN), time, cycle-slip flag
- For each epoch ([math]\displaystyle{ k }[/math])
- For each tracked satellite ([math]\displaystyle{ s }[/math])
- Declare cycle-slip when data hole greater than [math]\displaystyle{ tol_{\Delta t} }[/math] [footnotes 4].
- If no data hole larger than [math]\displaystyle{ tol_{\Delta t} }[/math], thence:
- Update an array with the last [math]\displaystyle{ N }[/math] differences of
- [math]\displaystyle{ d(s;k)=\Phi(s;k)-R(s;k) \qquad \mbox{(2)} }[/math]
- That is: [math]\displaystyle{ [d(s;k-N),\dots,d(s;k-1)] }[/math]
- Compute the mean and sigma discrepancy over the previous [math]\displaystyle{ N }[/math] epochs (after the last cycle-slip) [math]\displaystyle{ [k-N, \dots , k-1] }[/math]:
- [math]\displaystyle{
\begin{array}{l}
m_d(s;k-1)=\displaystyle \frac{1}{N} \sum_{i=1}^{N}{d(s;k-i)}\\
m_{d^2}(s;k-1)=\displaystyle \frac{1}{N}\sum_{i=1}^{N}{d^2(s;k-i)}\\
S_d(s;k-1)= \displaystyle \sqrt{m_{d^2}(s;k-1)-m_d^2(s;k-1)}
\end{array} \qquad \mbox{(3)}
}[/math]
- Compare the difference at the epoch [math]\displaystyle{ k }[/math] with the mean value of differences computed over the previous [math]\displaystyle{ N }[/math] samples window. If the value is over a [math]\displaystyle{ threshod=n_T*S_d }[/math] (e.g., [math]\displaystyle{ n_T=6 }[/math]), declare cycle-slip [footnotes 5].
- That is:
- If [math]\displaystyle{ |d(s;k)-m_d(s;k-1)| \gt n_T \,S_d(s;k-1) }[/math],
- Thence, cycle-slip.
- Reset algorithm after cycle slip.
- End
- For each tracked satellite ([math]\displaystyle{ s }[/math])
- End
- For each epoch ([math]\displaystyle{ k }[/math])
Comments:
- This algorithm can be seen as a particular case of the previous Example 1, using a zero-degree polynomial fit.
- This detector is affected by the pseudorange noise and multipath, as well as the divergence of the ionosphere. Thence, higher sampling rates improve the detection performance, but still the shortest jumps can escape to this detector. On the other hand, a minimum number of samples is needed for the filter initialisation, in order to assure a reliable value of [math]\displaystyle{ S_d }[/math] for the detection threshold.
- To avoid unrealistic estimations of sigma during the first iterations of the filter, the following weighted average with an initial value [math]\displaystyle{ S^2_0 }[/math] can be used (see in figure 1 an example of implementation performance):
- [math]\displaystyle{ S_d^2(s;k) = \frac{k-1}{k}S_d^2(s;k)+\frac{1}{k}S^2_0 \qquad \mbox{(4)} }[/math]
- where [math]\displaystyle{ S_0 }[/math] is a predefined initial value for sigma (e.g., [math]\displaystyle{ S_0=1m }[/math]).
- Another easier approach could be to fix a lower, or lower and upper bounds, for the sigma threshold.
- That is: to take [math]\displaystyle{ threshod=n_T*S_d }[/math], with [math]\displaystyle{ th_{min} \leq threshod \leq th_{max} }[/math].
- The Hatch filter can be used instead of the finite window of equations (3) to compute the mean values [math]\displaystyle{ m_d }[/math], [math]\displaystyle{ m_{d^2} }[/math], in order to simplify the code:
- [math]\displaystyle{ \begin{array}{l} m_d(s;k)= \displaystyle \frac{a-1}{a} m_d(s;k-1) + \frac{1}{a} d(s;k)\\ \end{array} \qquad \mbox{(5)} }[/math]
- where, [math]\displaystyle{ a=k }[/math] when [math]\displaystyle{ k\lt N }[/math] and [math]\displaystyle{ a=N }[/math] when [math]\displaystyle{ k \geq N }[/math].
- This equation allow computation of a sequential estimate of the mean value, but this filter has infinite memory, propagating forward the divergence of the ionospheric refraction [footnotes 6]. Nevertheless, such an accumulated effect, although biasing the ambiguity estimate, should not affect the cycle-slips detection, because it varies smoothly and the detector looks for large jumps.
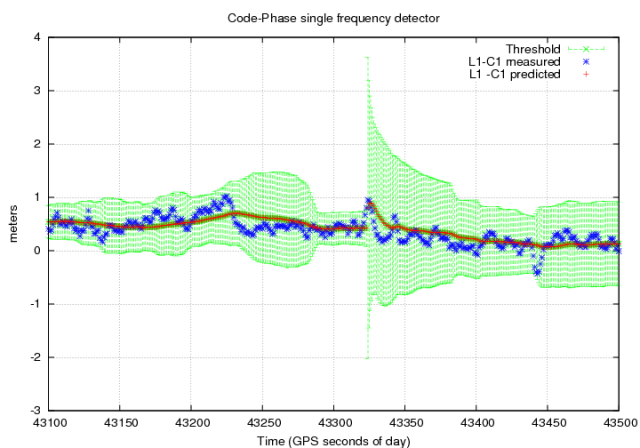 Figure 1: Fault cycle-slip detection on GPS [math]\displaystyle{ L_1 }[/math] signal: A multipath drift, after a quite stable period (i.e., with small sigma), produces a fault detection. The Measured and Predicted differences are compared with the confidence threshold (computed with the sliding window algorithm, using the equation (3) combined with (4).
Figure 1: Fault cycle-slip detection on GPS [math]\displaystyle{ L_1 }[/math] signal: A multipath drift, after a quite stable period (i.e., with small sigma), produces a fault detection. The Measured and Predicted differences are compared with the confidence threshold (computed with the sliding window algorithm, using the equation (3) combined with (4).
Additional comments: Differences in time detector.
A detector based in the n-order time differences of carrier phase [math]\displaystyle{ \Phi }[/math] measurements between consecutive epochs could be considered (see article Detector based in carrier phase data: The geometry-free combination. Nevertheless, it must be taken into account that such differences are affected by changes in range and in clocks [footnotes 7]. In spite of that, most of the geometric range variation is cancelled from [math]\displaystyle{ \Delta^3 }[/math], because it varies as a smooth function. Thence, this detector mainly affected by the receiver clock instabilities, high ionospheric fluctuations (i.e., scintillation...), as well.
In the case of the receiver clock effects, they can be removed by considering single differences of measurements between pairs of satellites in view, but it will enlarge the noise. The ionospheric effects will be not completely removed with such differences, but they should not be a problem, except for a highly disturbed scenario.
Notes
- ^ This approach is inspired in the algorithms developed by [Blewitt, 1990] for the geometry-free combination of two frequency signals. Notice that, a similar scheme is applied here for the code and phase combination of a single frequency signal.
- ^ For instance, 60 seconds.
- ^ [math]\displaystyle{ n=2 }[/math] or [math]\displaystyle{ 3 }[/math] can be used.
- ^ For instance, 15 seconds with 1 Hz data.
- ^ The mean bias between code and phase computed from the "previous [math]\displaystyle{ N }[/math] samples" is taken as the prediction of the actual difference at epoch [math]\displaystyle{ k }[/math] (i.e., [math]\displaystyle{ \hat{d}(s;k)\equiv m_d(s;k-1) }[/math]) with confidence [math]\displaystyle{ n_T\,S_d(s;k-1) }[/math].
- ^ On the contrary, the equations (3) provide and estimate based in a (sliding) window, with a finite number of points.
- ^ In the case of article Detector based in carrier phase data: The geometry-free combination, the geometry-free combination was used, cancelling all the non dispersive effects (geometric range, clocks...).
References
[Blewitt, 1990] Blewitt, G., 1990. An automatic editing Algorithms for GPS data. Geophysical Research Letters. 17(3), pp. 199-202.
