Ellipsoidal and Cartesian Coordinates Conversion

Fundamentals
Title	Ellipsoidal and Cartesian Coordinates Conversion
Author(s)	J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain.
Level	Advanced
Year of Publication	2011

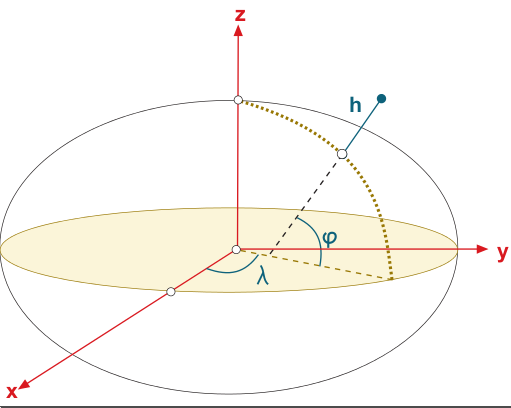
The [math]\displaystyle{ (x,y,z) }[/math] ECEF cartesian coordinates can be expressed in the ellipsoidal coordinates [math]\displaystyle{ (\varphi, \lambda, h) }[/math], where [math]\displaystyle{ \varphi }[/math] and [math]\displaystyle{ \lambda }[/math] are, respectively, the latitude and longitude from the ellipsoid, and [math]\displaystyle{ h }[/math] the height above it. Figure 1 illustrates the relation between Cartesian and ellipsoidal coordinates.

Figure 1: Cartesian [math]\displaystyle{ (x,y,z) }[/math] and ellipsoidal [math]\displaystyle{ (\varphi, \lambda, h) }[/math] coordinates

From Ellipsoidal to Cartesian coordinates

The Cartesian coordinates of a point [math]\displaystyle{ (x,y,z) }[/math] can be obtained from the ellipsoidal coordinates [math]\displaystyle{ (\varphi, \lambda, h) }[/math] by the next expressions:

[math]\displaystyle{ \begin{array}{l} x=(N+h) \cos \varphi\,\cos \lambda\\ y=(N+h)\cos \varphi\,\sin \lambda\\ z=\left ((1-e^2)N+h \right)\sin \varphi\\ \end{array} \qquad \mbox{(1)} }[/math]

where [math]\displaystyle{ N }[/math] is the radius of curvature in the prime vertical:

[math]\displaystyle{ N=\displaystyle \frac{a}{\sqrt{1-e^2\sin^2\varphi}} \qquad \mbox{(2)} }[/math]

and where the eccentricity [math]\displaystyle{ e }[/math] is related with the semi-major axis [math]\displaystyle{ a }[/math], the semi-minor axis [math]\displaystyle{ b }[/math] and the flattening factor [math]\displaystyle{ f = 1 -\frac{b}{a} }[/math] by:

[math]\displaystyle{ e^2=\displaystyle \frac{a^2-b^2}{a^2}=2f-f^2 \qquad \mbox{(3)} }[/math]

From Cartesian to Ellipsoidal coordinates

The ellipsoidal coordinates of a point [math]\displaystyle{ (\varphi, \lambda, h) }[/math] can be obtained from the cartesian coordinates [math]\displaystyle{ (x,y,z) }[/math] as follows:

The longitude [math]\displaystyle{ \lambda }[/math] is given by: [math]\displaystyle{ \lambda= arctan2(y,x) \qquad \mbox{(4)} }[/math]

The latitude is computed by an iterative procedure.

1. The initial value is given by:

[math]\displaystyle{ \varphi_{(0)}=\arctan\left [ \frac{z}{(1-e^2)\,p} \right ] \qquad \mbox{(5)} }[/math]

with [math]\displaystyle{ p=\sqrt{x^2+y^2} }[/math].

2. Improved values of [math]\displaystyle{ \varphi }[/math], as well as the height [math]\displaystyle{ h }[/math], are computed iterating in the equations:

[math]\displaystyle{ \begin{array}{l} N_{{(i)}}= \frac{a}{\sqrt{1-e^2\sin^2\varphi_{_{(i-1)}}}}\\[0.6cm] h_{{(i)}}=\frac{p}{\cos \varphi_{_{(i-1)}}}-N_{(i)}\\[0.5cm] \varphi_{{(i)}}= \arctan\left [ \frac{z}{ \left ( 1 - e^2\frac{N_{(i)}}{N_{(i)}+h_{(i)}} \right ) p } \right ] \end{array} \qquad \mbox{(6)} }[/math]

The iterations are repeated until the change between two successive values of [math]\displaystyle{ \varphi_{(i)} }[/math] are smaller than the precision required.