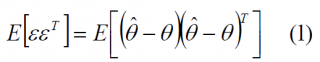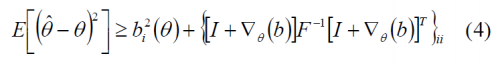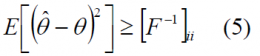If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Cramér Rao Lower Bound
| Fundamentals | |
|---|---|
| Title | Cramér Rao Lower Bound |
| Author(s) | J.A. Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
The mean-squared error for any estimate of a nonrandom parameter has a lower bound, known in the literature as the Cramér-Rao lower bound or CRLB in short [J.-A. Avila-Rodriguez et al., 2006][1]. The Cramér-Rao lower bound defines the ultimate accuracy of any estimation and shows the minimum code pseudorange variance we would have with the best possible receiver implementation. Indeed, the Cramér-Rao lower bound is nothing else than a different way of expressing the Gabor bandwidth which sets the physical limit of a signal for a given bandwidth. This last one is also known in the literature as the root mean square bandwidth.
In our particular case, we are interested in finding the bound of the matrix:
being [math]\displaystyle{ \epsilon }[/math] the code delay error, [math]\displaystyle{ \theta }[/math] the real code delay value and [math]\displaystyle{ \hat{\theta} }[/math] its estimation. As it can be shown, the Cramér-Rao lower bound is deeply related to the Fisher information matrix F in the following form:
where [math]\displaystyle{ b\left(\theta\right) }[/math] is the bias of the estimate [math]\displaystyle{ \theta }[/math] and F is the already mentioned Fisher matrix defined by means of the Hessian matrix as follows
It must be noted that according to this general definition, the Cramér-Rao lower bound also applies for the case of biased estimates in contrast to the way it is widely used in the general literature where the Cramér-Rao lower bound is understood as the minimum unbiased variance estimate bound.
Looking now at the bound of every parameter in particular, the Cramér-Rao lower bound can be expressed as follows:
and for the case the estimator is unbiased, the bound simplifies then to
The most important conclusion that can be drawn from observing the equation above is that for the unbiased case, the estimator is not necessary for the computation of the bound. In fact, we only need the Fisher matrix to compute the CRLB, which only depends on the logarithm of the likelihood function. In other words, only in the case of unbiased estimators the Cramér-Rao lower bound is independent of the used estimator. Accordingly, using the unbiased Cramér-Rao lower bound when the estimator is biased can lead to wrong conclusions.
Indeed, due to its simplicity, the unbiased Cramér-Rao lower bound is frequently used to assess performance limits. Nevertheless, we must keep in mind that when multipath is present the exact form of the estimator´s bias explicitly enters the computation of the bound. As a consequence, the use of the unbiased Cramér-Rao has to be actually understood as a desperate try to give a lower bound to a problem which is in reality so complicated and nonlinear that computing the bias is nearly impossible
References
- ^ [J.-A. Avila-Rodriguez et al., 2006] J.-A. Avila-Rodriguez, S. Wallner, G.W. Hein, How to Optimize GNSS Signals and Codes for Indoor Positioning, Proceedings of the International Technical Meeting of the Institute of Navigation, ION-GNSS 2006, 26-29 September, 2006, Fort Worth Convention Center, Fort Worth, Texas.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)