GNSS Basic Observables

Fundamentals
Title	GNSS Basic Observables
Author(s)	J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain.
Level	Basic
Year of Publication	2011

Pseudorange

The basic GNSS observable is the travelling time [math]\displaystyle{ \Delta T }[/math] of the signal to propagate from the phase centre of the satellite antenna (at the emission time) to the phase centre of the receiver (at the reception time). This value multiplied by the speed of light gives us the apparent range [math]\displaystyle{ D=c\,\Delta T }[/math] between them.

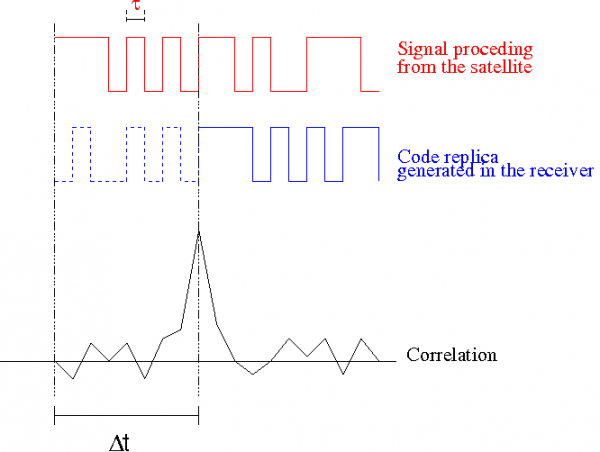
As commented in article GNSS signal, the GNSS signals contain ranging codes to allow the users to compute the travelling time [math]\displaystyle{ \Delta T }[/math]. Indeed, the receiver determines [math]\displaystyle{ \Delta T }[/math] correlating the received code ([math]\displaystyle{ P }[/math]) from the satellite with a replica of it generated in the receiver, so this replica is moved in time ([math]\displaystyle{ \Delta T }[/math]) until the maximum correlation is obtained (see figure 1).

Figure 1: Determination of the signal travelling time.

This measurement [math]\displaystyle{ D= c\Delta T }[/math] is what we know as pseudorange or pseudodistance and it is an "apparent range" between the satellite and the receiver that does not match with its geometric distance due to, among other factors, synchronism errors between receiver and satellite clocks. Taking explicitly into account possible synchronism errors between these clocks, the travelling time between transmission and reception is obtained as a difference of times measured in two different clocks or time scales: the satellite ([math]\displaystyle{ t^s }[/math]) and the receiver ([math]\displaystyle{ t_r }[/math]). Thence, considering a reference time scale [math]\displaystyle{ T }[/math], which we will call GNSS (i.e., GPS, GLONASS, Galileo), the pseudorange measurement for satellite [math]\displaystyle{ s }[/math] and receiver [math]\displaystyle{ r }[/math] may be expressed as:

[math]\displaystyle{ R_{_P}(t)=c\ [t_r(T_2)-t^s(T_1)] }[/math]

Where:

• [math]\displaystyle{ c }[/math] is the speed of light in a vacuum.
• [math]\displaystyle{ t_r(T_2) }[/math] is the time of signal reception, measured in the time scale given by the clock of receiver [math]\displaystyle{ r }[/math].
• [math]\displaystyle{ t^s(T_1) }[/math] is the time of signal transmission, measured in the time scale given by the satellite clock [math]\displaystyle{ s }[/math].

The Pseudorange [math]\displaystyle{ R_{_P} }[/math] measurement obtained by the receiver using this procedure includes, besides geometric range [math]\displaystyle{ \rho }[/math] between the receiver and the satellite and clock synchronism errors, other terms due to signal propagation through the atmosphere (ionosphere and troposphere), relativistic effects, instrumental delays (of satellite and receiver), multipath and receiver noise (see GNSS Measurements Modelling). Taking explicitly into account all these terms, the previous equation can be rewritten as follows, where [math]\displaystyle{ R_{_P} }[/math] represents any GNSS code measurement at frequency [math]\displaystyle{ f }[/math] (from GPS, GLONASS, Galileo, etc.):

[math]\displaystyle{ R_{_P}=\rho+c(dt_r-dt^s)+T+\alpha_f\,STEC+K_{P,r}-{K_P}^s+\mathcal{M}_P+\varepsilon_{_P} }[/math]

• [math]\displaystyle{ \rho }[/math] is the geometric range between the satellite and receiver antenna phase centres at emission and reception time, respectively (see article Geometric Range Modelling). Note: The Antenna Phase Centre (APC) is frequency dependent, but we neglect this effect here for simplicity (see article Antenna Phase Centre).

• [math]\displaystyle{ dt_r }[/math] and [math]\displaystyle{ dt^s }[/math] are the receiver and satellite clock offsets from the GNSS time scale, including the relativistic satellite clock correction (see Clock Modelling).

• [math]\displaystyle{ T }[/math] is the tropospheric delay, which is non-dispersive (see Tropospheric Delay).

• [math]\displaystyle{ \alpha_f\, STEC }[/math] is a frequency-dependent ionospheric delay term, where [math]\displaystyle{ \alpha_f }[/math] is the conversion factor between the integrated electron density along the ray path [math]\displaystyle{ STEC }[/math], and the signal delay at frequency [math]\displaystyle{ f }[/math]. That is, [math]\displaystyle{ \alpha_f=\frac{40.3}{f^2}10^{16}\; m_{\mbox{ signal delay}_{(\mbox{ at frequency}f)}}/_{TECU} }[/math], where the frequency [math]\displaystyle{ f }[/math] is in [math]\displaystyle{ Hz }[/math] and [math]\displaystyle{ 1\, TECU=10^{16}e^-/m^2 }[/math].(See article Ionospheric Delay).

• [math]\displaystyle{ K_{P,r} }[/math] and [math]\displaystyle{ {K_P}^s }[/math] are the receiver and satellite instrumental delays, which are dependent on the code and frequency (see articles Combination of GNSS Measurements and Instrumental Delay).

• [math]\displaystyle{ \mathcal{M}_P }[/math] represents the effect of multipath, also depending on the code and frequency, and [math]\displaystyle{ \varepsilon_{_P} }[/math] is the receiver noise (see article GNSS Measurement features and noise).

Carrier phase

Besides the code, the carrier phase itself is also used to obtain a measure of the apparent distance between satellite and receiver. These carrier phase measurements are much more precise than the code measurements (typically two orders of magnitude more precise), but they are ambiguous by an unknown integer number of wavelengths [math]\displaystyle{ (\lambda N }[/math]). Indeed, this ambiguity changes arbitrarily every time the receiver loss the lock on the signal, producing jumps or range discontinuities.

The carrier phase measurements ([math]\displaystyle{ \Phi_L=\lambda_L\,\phi_L }[/math]) can be modeled as:

[math]\displaystyle{ \Phi_L=\rho+c(dt_r-dt^s)+T-\alpha_f \, STEC+k_{L,r}-{k_L}^s+\lambda_L\,N_L+\lambda_L \,w+m_L+\epsilon_{_L} }[/math]

where, besides the terms seen in equation (2), it includes the wind-up ([math]\displaystyle{ \lambda_L \,w }[/math]) due to the circular polarisation of the electromagnetic signal and the integer ambiguity [math]\displaystyle{ N_L }[/math] (see GNSS Measurement features and noise).

The terms [math]\displaystyle{ k_{L,r} }[/math] and [math]\displaystyle{ {k_L}^s }[/math] are frequency dependent and corresponds to carrier phase instrumental delays (see Undifferenced Ambiguity Fixing) associated to the receiver and satellite, respectively. The [math]\displaystyle{ m_L }[/math] and [math]\displaystyle{ \epsilon_L }[/math] terms are the carrier phase multipath and noise.

Notice that the ionospheric term has opposite sign for code and phase. This means that the ionosphere produces an advance of the carrier phase measurement equal to the delay on the code measurements (see Ionospheric Delay).

Doppler shift

The receiver must estimate the Doppler shift of each received signal in order to be able to receive it. The Doppler shift of a given signal is the time derivative of its carrier phase. As such, the Doppler shift is primarily determined by the relative velocity of the satellite's and receiver's antennas, plus a common offset that is proportional to the receiver's clock frequency error.