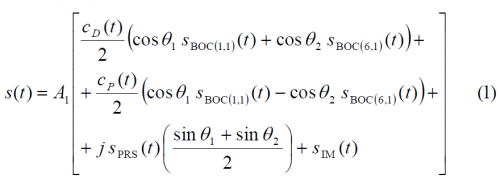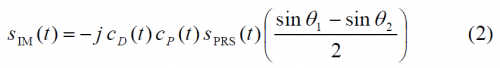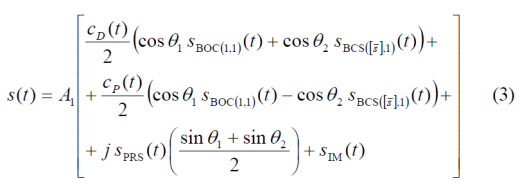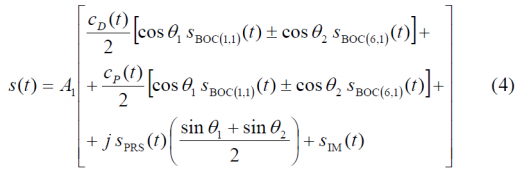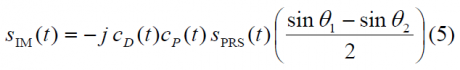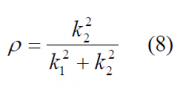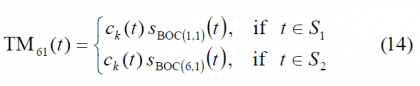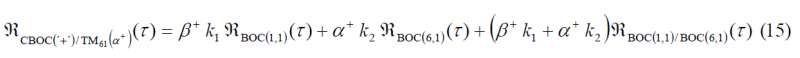If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Composite BOC (CBOC)
| Fundamentals | |
|---|---|
| Title | Composite BOC (CBOC) |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
CBOC Implementation
The CBOC implementation is a particular case of the CBCS Modulation. The CBOC modulation can be expressed as follows
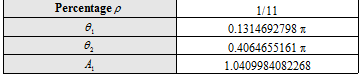
where we can recognize that in this particular case the BCS component is BOC(6,1) with a percentage of power of 1/11. Furthermore the high frequency signal is placed on both the data and pilot channels and equal power for both channels is assumed. In addition, the total Galileo Open Service (OS) power is equal to that of the PRS and the modulation parameters are the following:
Optimal Tracking of CBOC
As one can imagine, until the final Galileo implementation of MBOC was selected, different CBOC implementations were under consideration. In the next lines we summarize the main results of the analyses carried out to optimally track CBOC each of the proposed solutions.
Following the results from [O. Julien et al., 2006][1] we will show in this chapter the tracking performance of the CBOC modulation when only one channel of the Galileo E1 OS (data or pilot) is used. As we have seen above, there are many ways of implementing MBOC and even if we would constrain our analysis to CBOC, it can be shown that the variety of solutions is still broad. Indeed, the high frequency BOC(6,1) component could go in principle on both data and pilot channels, only on the pilot, only on the data, the power splits could change, and they all would still fulfil the MBOC definition that we gave above. To simplify thus our analysis, the three main cases are exposed next. These correspond basically to the three CBOC implementations that were considered for the Galileo E1 OS:
- The use of a CBOC(6,1,1/11) where both the data and pilot channels have a BOC(6,1) component in anti-phase. In this case, the power of the BOC(6,1) part is 1/11 of the channel total power. This is the implementation finally selected for Galileo E1 OS.
- The use of a CBOC(6,1,2/11) where only one of the channels, the pilot or the data, has a BOC(6,1) component with alternating sign, while the other channel is a pure BOC(1,1). In this case, the power of the BOC(6,1) part is 2/11 of the pilot channel total power. Moreover, it is important to note that the alternation of BOC(6,1) is necessary to get rid of the cross spectral terms that would result otherwise. This will be shown in the following lines.
- CBOC(6,1,1/11) is used on both the data and pilot channels, being BOC(6,1) in both channels with alternating sign. In this case, the data and pilot channels have a BOC(6,1) power of 1/11 of the channel total power.
Recalling now the general CBCS definition from:
and substituting BCS by BOC(6,1) we can define the general CBOC model as follows:
and looking only at the pilot channel for the three cases described above, we have:
where indicates the amount of power on the high frequency BOC(6,1) component:
The last model to introduce is the alternating model, which is shown to be:
for even chips, and
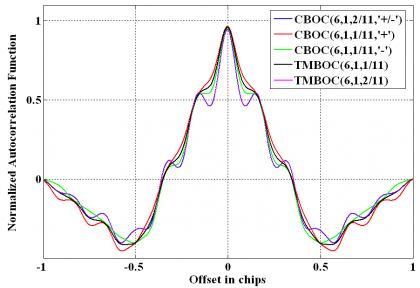
for odd chips. The autocorrelation function of the three models is shown next:
As we can see, the two first auto-correlations present an additional cross-term due to the existence of cross-correlation between BOC(1,1) and BOC(6,1). As we mentioned above, this cross-term is not desirable and must be eliminated to generate a spectrum according to the MBOC definition. This is possible if data and pilot are in anti-phase (each with a different sign) or if the BOC(6,1) component alternates its sign. Nonetheless, we will keep these signals for reference in the following figures to show the performance. We show next the autocorrelation functions of the different analyzed solutions compared with the TMBOC solution for a receiver bandwidth of 24 MHz:
As we can recognize in the figure above, the shape of the auto-correlation function highly depends on the amount of power on BOC(6,1). Indeed, the higher the value of , the more ripples the auto-correlation will present and the better the potential performance will be. Furthermore, it is interesting to see that the sharpest slope around the origin is shown by TMBOC and the version while TMBOC(6,1,2/11) and perform similar. MBOC is analyzed next regarding the following three criteria:
- False tracking points
- Code tracking noise
- Multipath-induced code tracking error
False Tracking Points
If we take a closer look at the auto-correlation function of Figure 1 above, it is clear to recognize the existence of secondary peaks that could lead to stable false locks. Indeed, the more ripples the function presents and the more accentuated the undulations are, the higher the probability that we lock on a non-desired but stable tracking point. Fortunately, not all the solutions are equally susceptible to suffering from this effect, since this depends actually on how the auto-correlation function looks like. In fact, while the selected CBOC(1/11) for Galileo E1 OS is not likely to lead to stable false lock points as shown in [J.-A. Avila-Rodriguez et al., 2006][2], the existence of false lock points would be nearly unavoidable for the implementation, implying thus a higher complexity to detect the right peak. This is in fact the prize for allocating more BOC(6,1) power on the channel. Finally, it is important to note that no matter which of the implementations we look at, since BOC(1,1) is the dominant signal in all of them, a false lock detector is still necessary in order to make sure that the receiver is tracking the signal based on the correct autocorrelation main peak, and not the secondary of BOC(1,1).
Thermal Noise-Induced Code Tracking Error
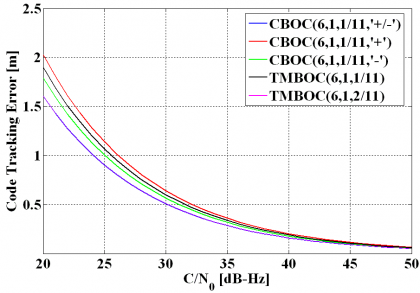
In order to understand how the code tracking noise behaves for the different implementations of MBOC, we present in the next figure the Cramér Rao Lower Bound.
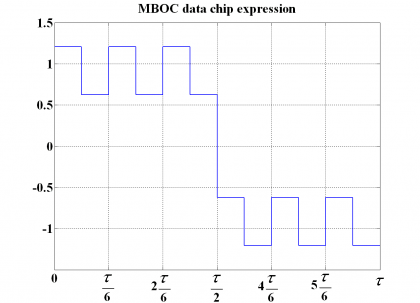
As we can see, the best performance corresponds to the alternating version with 2/11 of power on BOC(6,1) or to its equivalent TMBOC version, since these can take advantage of the high frequency components of the signal the best. Moreover, among the different CBOC solutions with the 1/11 of average power that results from considering data and pilot together, the worst performance is shown to be that of the in-phase solution while the anti-phase is the best. This was to expect since its autocorrelation function’s main peak has the steepest slope. We can also see this if we compare both phase and anti-phase versions in the time domain.
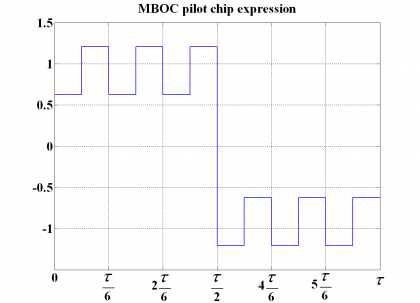
Equally, the pilot channel would present the following shape for a chip.
From the previous figures it is easy to recognize that the pilot channel will have more components at higher frequencies since at 0.5 chips the amplitude variation is higher. Furthermore, the alternating CBOC solution with 1/11 of power on BOC(6,1) performs as the average of the phase and anti-phase solutions shown above. To avoid any confusion, it is important to underline that the solutions studied above correspond to MBOC implementations that were object of study during the design of Galileo E1 OS and GPS L1C. The finally selected CBOC implementation of Galileo has BOC(6,1) on both data and pilot, being these in anti-phase with respect to each other. According to the previous notation, this means that the pilot channel of Galileo E1 OS will be and the data channel .
Multipath Induced Tracking Error
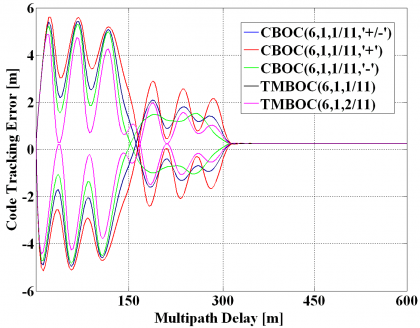
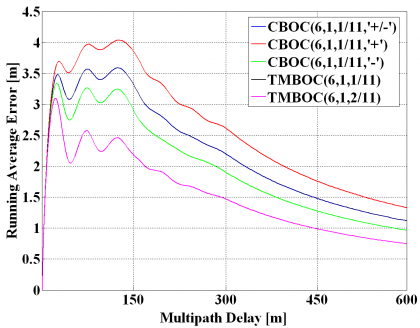
The multipath performance of a signal highly depends on the shape of the auto-correlation function. Indeed, this was one of the aspects that were more seriously taken into consideration during the optimization of the Galileo Open Service and GPS Civil signals in E1/L1. We show in the next figures the multipath performance of different MBOC implementations by means of the multipath envelopes and the multipath running average error as done in [G.W. Hein et al., 2006a][3] and [G.W. Hein et al., 2006b][4]. Note that TMBOC(6,1,1/11) and perform the same and therefore are overlapped in the next figures.
As we can see, for an early-late spacing of 0.1 chips and a one-sided front-end filter of 12 MHz, the best performance is exhibited by , followed by , and . Moreover, it is clear to see that all the solutions clearly outperform BOC(1,1). In addition, it is important to note that and TMBOC(6,1,1/11) perform the same in average when both data and pilot are processed in the receiver.
Conclusions on Optimal CBOC Tracking
As we have seen in previous lines, the best CBOC implementation of MBOC in terms of performance is the anti-phase solution. Nevertheless, as demonstrated in (12), this solution presents the great inconvenient of showing a non desired cross-term that can only be eliminated if the other channel adopts the counterpart . This is indeed the case in the finally selected CBOC implementation of Galileo E1 OS. Then, the total performance of this CBOC implementation, seen as data and pilot together, is equivalent to that of the alternating solution.
Another studied option was to use directly the solution on both the data and pilot channels, in which case both channels would have the same tracking performance. This implementation would perfectly fulfil the MBOC spectrum too but the drawback was be the extra complexity required for the implementation of the alternation. Equally, the option of using a on one channel and a pure BOC(1,1) on the other channel would permit to have one channel with excellent tracking performance, while the other channel would just use a pure BOC(1,1) modulation. This signal would be of interest for some types of receivers with a philosophy behind very much in line with how TMBOC is conceived.
All the figures that we have shown above rely on the assumption that a CBOC replica signal has to be locally generated by the receiver. Indeed, CBOC is a linear combination of two sub-carriers and has thus more than two levels, so that 2 bits are needed to encode the signal. While this should not be a great challenge as some works have already shown [P.G. Mattos, 2007][5], we will study in the next chapter a suboptimal tracking of CBOC using local replicas encoded with only 1 bit, as shown in [J.-A. Avila-Rodriguez et al., 2006] [2] and [O. Julien et al., 2006] [1]. One could of course think of separating the correlation of the incoming CBOC signal with a pure BOC(1,1) replica and, on the other side, with a pure BOC(6,1) replica. Then a simple linear combination of the outputs of both correlators would be sufficient to obtain the same result as if we had correlated directly with the CBOC replica of two bits. However, this processing requires twice as many correlators as the traditional CBOC tracking. In the next lines we present a solution that avoids to have to pay this prize [O. Julien et al., 2006][1] and [J.-A. Avila-Rodriguez et al., 2006] [2].
Suboptimal Tracking of CBOC: TMBOC like approach
As shown in [J.-A. Avila-Rodriguez et al., 2006] [2], the idea behind the 1-bit receiver technique is to correlate the incoming CBOC signal with a locally generated signal obtained by time-multiplexing a BOC(1,1) sub-carrier and a BOC(6,1) sub-carrier. We can model this replica as follows:
where [math]\displaystyle{ S_1 }[/math] is the union of the segments of time when a BOC(1,1) sub-carrier is used. Equally, [math]\displaystyle{ S_2 }[/math], the complement of [math]\displaystyle{ S_1 }[/math] in the time domain, is the union of the segments of time when a BOC(6,1) sub-carrier is generated. In addition, we write [math]\displaystyle{ TM_{61} }[/math] in order to distinguish this technique from the typical CBOC replica approach studied above. The advantage of this approach is that by using such a replica we only need to encode with 1 bit reducing thus the complexity of the receiver. Moreover, time-multiplexing reduces the number of correlators.
Let us define [math]\displaystyle{ \alpha }[/math] to designate the percentage of time that the BOC(6,1) sub-carrier is used in one code length, and [math]\displaystyle{ \beta = 1 - \alpha }[/math] to represent the amount of time reserved for the BOC(1,1) local sub-carrier part. Furthermore, we will assume that the sign of the BOC(6,1) local sub-carrier in the local replica is taken according to the sign of the BOC(6,1) used in the CBOC signal. This means that for the case the CBOC channel is in-phase, we have a positive sign and thus the percentage of BOC(6,1) time is given by [math]\displaystyle{ \alpha^+ = 1 -\beta^+ }[/math]. Equally, for the anti-phase CBOC component the percentage of BOC(6,1) time is given by [math]\displaystyle{ \alpha^- = 1 -\beta^- }[/math]. It must be noted that [math]\displaystyle{ \alpha^+ }[/math] and [math]\displaystyle{ \alpha^- }[/math] can be different in general. As a result, the cross-correlation that results from using the [math]\displaystyle{ TM_61 }[/math] replica with the different CBOC implementations of previous chapter is given by the following expressions:
As we can see in the expressions above, the correlation functions of BOC(1,1) and BOC(6,1) are also weighted as was also the case for the CBOC replica, with the difference that the weights are in this case controlled by the factors [math]\displaystyle{ \alpha }[/math] and [math]\displaystyle{ \beta }[/math] and the cross-correlation between [math]\displaystyle{ TM_{61} }[/math] and CBOC induces additional correlation losses as shown in [O. Julien et al., 2006] [1] and [J.-A. Avila-Rodriguez et al., 2006c].
It is also interesting to see in [O. Julien et al., 2006][1] and [J.-A. Avila-Rodriguez et al., 2006][2] that if the Dot Product (DP) discriminator is employed, different TM61 replicas could be used for the prompt correlator and for the early and late correlators. Indeed, for the particular case of the DP discriminator, the prompt correlator only affects the tracking noise squaring losses and is thus recommendable to choose a local prompt replica that minimizes the correlation loss with the incoming CBOC signal. As shown in [J.-A. Avila-Rodriguez et al., 2006][2], this can be achieved by selecting [math]\displaystyle{ \alpha=0 }[/math] or what is equivalent, by using a pure BOC(1,1) sub-carrier as proposed in [J.-A. Avila-Rodriguez et al., 2006][2].
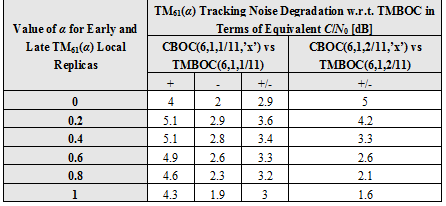
On the other hand, the early and late correlator outputs determine the gain of the discriminator as well as the noise correlation between the early and late correlators’ output. Next table shows the tracking noise degradation that results from the use of the TM61 technique for the different studied CBOC cases and we compare it with the optimal TMBOC tracking for the same BOC(6,1) power [O. Julien et al., 2006][1].
As we can see, for CBOC(1/11) the most interesting values are either a high or a low value of , since for those cases the equivalent C/N0 degradation of the tracking noise is the lowest with a value of 1.9 dB for the , of 3 dB for the and of 4 dB for the . It is important to note that [math]\displaystyle{ \alpha=0 }[/math] implies to use a pure BOC(1,1) replica and [math]\displaystyle{ \alpha=1 }[/math] a pure BOC(6,1) replica.
In the same manner, the best option for and TMBOC(6,1,2/11) would be to take a value of [math]\displaystyle{ \alpha }[/math]as high as possible. This means, a pure BOC(6,1) replica for the E-L correlators would be the ideal choice in this case. As a conclusion, in order to have a common architecture for CBOC(6,1,1/11), CBOC(6,1,2/11) and TMBOC(6,1,2/11), the best would be to select a [math]\displaystyle{ TM_{61} }[/math] tracking technique that would only use pure local replicas: BOC(1,1) for the prompt correlator and BOC(6,1) for the E-L correlators. Moreover, no time-multiplexing would be needed any more, simplifying thus the complexity of the receiver. As one can imagine, if this approach is valid for the different MBOC implementations discussed in previous pages, it is also valid for the particular CBOC and TMBOC solutions adopted by Galileo and GPS.
Another aspect that we have not touched yet is the multipath rejection of the different discussed TM61 options. As shown in [O. Julien et al., 2006][1]for both the CBOC(1/11) and the CBOC(2/11) cases, a value of [math]\displaystyle{ \alpha }[/math] around 0.5 would lead to the best results. Nevertheless, values of [math]\displaystyle{ \alpha }[/math] close to 1 would also deliver performances close to the optimum. In addition, using [math]\displaystyle{ \alpha=0 }[/math] is shown to be suboptimal in terms of multipath rejection since the performance is then that of BOC(1,1) [J.-A. Avila-Rodriguez et al., 2006][2].
As a conclusion, it seems that a sub-optimum implementation of a CBOC-TMBOC receiver based on a 1 bit architecture could use a pure local BOC(1,1) replica for the prompt correlator and a pure local BOC(6,1) replica for the early and late correlators. Moreover, we have seen that this scheme provides with relatively low degradation in terms of code tracking noise compared to the optimal TMBOC tracking.
The preceding derivations pursued to show that processing CBOC with a1 bit receiver is possible already today at the cost of some degradation. However, 2-bit receivers are already reality as shown in [P.G. Mattos, 2007] [5] and an optimal processing with 2 bits would be thus preferred. This would additionally imply some superiority of CBOC with respect to the TMBOC implementation since no blanking would be needed any more. Indeed, blanking of the BOC(6,1) pulses to avoid correlation losses is equivalent to reducing the equivalent code length by a factor 29/33 of the total length (10230). It must be noted though that this supposes a minimum additional complexity.
References
- ^ a b c d e f g [O. Julien et al., 2006] O. Julien, C. Macabiau, L. Ries, J.-L. Issler, 1 - Bit processing of Composite BOC (CBOC) Signals, First CNES Workshop on Galileo Signals and Signal Processing, 12-13 October 2006, IAS ( Institut Aero Spatial ) Toulouse, France.
- ^ a b c d e f g h [J.-A. Avila-Rodriguez et al., 2006] J.-A. Avila-Rodriguez, S. Wallner, G.W. Hein, E. Rebeyrol, O. Julien, C. Macabiau, L. Ries, A. DeLatour, L. Lestarquit, J.-L. Issler, CBOC – An Implementation of MBOC, First CNES Workshop on Galileo Signals and Signal Processing, 12-13 October 2006, IAS ( Institut Aero Spatial ) Toulouse, France.
- ^ [G.W. Hein et al., 2006a] G. W. Hein, J.-A. Avila-Rodriguez, S. Wallner, A.R. Pratt, J.I.R. Owen, J.-L Issler, J.W. Betz, C.J. Hegarty, S. Lenahan, J.J. Rushanan, A.L. Kraay, T.A. Stansell, MBOC: The New Optimized Spreading Modulation Recommended for Galileo L1 OS and GPS L1C, Proceedings of the International Technical Meeting of the Institute of Navigation, IEEE/ION PLANS 2006, 24-27 April, 2006, Loews Coronado Bay Resort, San Diego, California, USA.
- ^ [G.W. Hein et al., 2006b] G. W. Hein, J.-A. Avila-Rodriguez, S. Wallner, A.R. Pratt, J.I.R. Owen, J.-L Issler, J.W. Betz, C.J. Hegarty, S. Lenahan, J.J. Rushanan, A.L. Kraay, T.A. Stansell, MBOC: The New Optimized Spreading Modulation Recommended for Galileo L1 OS and GPS L1C, Inside GNSS – Working Papers, Vol.1, No.4, May/June 2006, pp.57-65.
- ^ a b [P.G. Mattos, 2007] P.G. Mattos, Hardware and Algorithm Implications of Adding Galileo Capability to an SPS GPS Receiver, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 2007, January 2007, San Diego, California, USA.