If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Satellite Coordinates
| Fundamentals | |
|---|---|
| Title | Satellite Coordinates |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
As the measurements are linked to the signal reception time, which is given by the receiver time tags (i.e., in the receiver clock), an algorithm is needed to obtain the signal emission time in the GNSS (GPS, GLONASS, Galileo...) time scale [footnotes 1]. Two algorithms are presented in Emission Time Computation to compute the transmission time, one of them based in the pseudorange measurement, and the other on a pure geometric approach.
Once, the transmission time is obtained, thence the satellites coordinates can be computed. This computation can be done in either, an inertial or a rotating earth-fixed Earth-Centred, Earth-Fixed (ECEF) coordinate frame. Obviously, an ECEF frame is more suitable for providing the user position on the earth and, therefore, this system is used as a reference frame for the satellite and receiver coordinates.
Such ECEF frame is taken at the reception time, because it is a common reference for all measurements[footnotes 2]. Thence, the earth rotation during the signal traveling time must be considered to account for the ECEF rotation during this elapsed time. An algorithm for this computation is given in Satellite Coordinates Computation.
Finally, beside the satellite coordinates (at the transmission time), the receiver coordinates (at the reception time) are also needed to compute the geometric range (from equation 1).
- [math]\displaystyle{ \rho_{rcv}^{sat}=\left\| {\mathbf r}_{rcv}-{\mathbf r}^{sat}\right \|=\sqrt{(x_{rcv}-x^{sat})^2+(y_{rcv}-y^{sat})^2+(z_{rcv}-z^{sat})^2} \qquad \mbox{(1)} }[/math]
The receiver coordinates are the unknowns to determine in the navigation problem and can seem quite contradictory to need some "knowledge of them to estimate them self" (i.e., to compute the receiver position). As it is explained in Code Based Positioning (SPP), a simple approach to solve the navigation problem is to initialise the positioning algorithm with an approximated user position [footnotes 3]. In this approach, the unknowns to estimate are the deviations of such approximate user location from the true coordinates, what is the same, the correction to apply in order to obtain the more accurate receiver coordinates.
Different options can be considered to obtain an initial value for the receiver coordinates, i.e., an user location "a priori", to initialise the navigation algorithm. The simplest way would be just to use the earth centre coordinates, i.e.,(0; 0; 0), or and arbitrary point on the earth surface, as well. After few number of iterations, the solution will converge to the actual receiver position. A nice approach is the Bancroft Method.
Notes
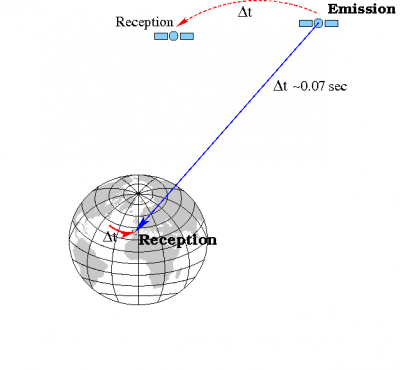
- ^ The satellite speed is about 5 km/s and traveling time about 0.1 s, then satellites move hundred of meters during signal flight time, see Figure 1.
- ^ Notice that reception time is common for all satellites, but not transmission time, which depends of the satellite-receiver range and, thence, is different for each satellite.
- ^ These approximate coordinates [math]\displaystyle{ (x_0, y_0, z_0) }[/math] or "a priories" are used to linearise the geometric range in the neighbourhood of this point (i.e., [math]\displaystyle{ \rho= \rho_0+ \nabla \rho|_{_{{\mathbf r}={\mathbf r}_0}}\cdot\Delta {\mathbf r} }[/math], where [math]\displaystyle{ \Delta {\mathbf r}=[\Delta x,\Delta y, \Delta z]^t }[/math]). This is done in order to build a linear model for position estimation, being the deviations from this nominal value [math]\displaystyle{ \Delta x= x-x_0, \Delta y= y-y_0, \Delta z=z-z_0 }[/math] the unknowns to estimate, together with the receiver clock offset [math]\displaystyle{ \delta t }[/math], and other parameters as well (see Solving Navigation Equations).