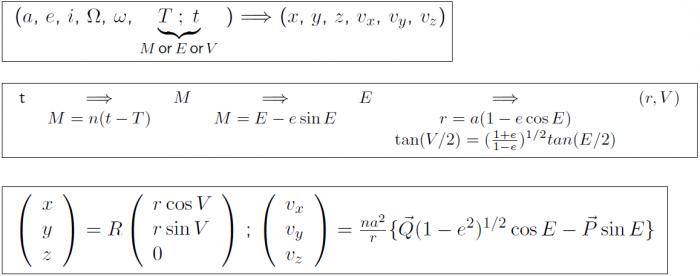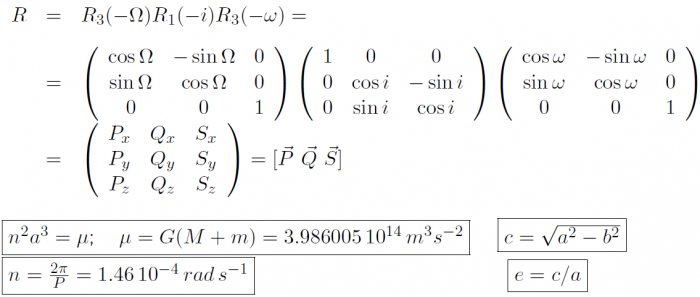If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Osculating Elements: Difference between revisions
Jump to navigation
Jump to search
Carlos.Lopez (talk | contribs) No edit summary |
Carlos.Lopez (talk | contribs) No edit summary |
||
| Line 15: | Line 15: | ||
::<math> (x, y, z, v_x, v_y, v_z) \Longrightarrow (a, e, i, \Omega, \omega, M) </math> | ::<math> (x, y, z, v_x, v_y, v_z) \Longrightarrow (a, e, i, \Omega, \omega, M) \qquad \mbox{(1)}</math> | ||
::<math> \vec c= \vec r \times \vec v \Longrightarrow p=\frac{c^2}{\mu} \Longrightarrow p \qquad \mbox{(2)}</math> | |||
::<math> v^2=\mu (2/r -1/a) \Longrightarrow a \qquad \mbox{(3)}</math> | |||
::<math> v^2=\mu (2/r -1/a) \Longrightarrow a </math> | |||
::<math> p=a(1-e^2) \Longrightarrow e </math> | ::<math> p=a(1-e^2) \Longrightarrow e \qquad \mbox{(4)}</math> | ||
::<math> \vec c = c \vec S \Longrightarrow \Omega=\arctan(-c_x/c_y); i=arcs(c_z/c) \Longrightarrow \Omega, i </math> | |||
::<math> \vec c = c \vec S \Longrightarrow \Omega=\arctan(-c_x/c_y); i=arcs(c_z/c) \Longrightarrow \Omega, i \qquad \mbox{(5)}</math> | |||
| Line 48: | Line 51: | ||
\end{array} | \end{array} | ||
\right) | \right) | ||
\Rightarrow \omega+V | \Rightarrow \omega+V | ||
\qquad \mbox{(6)} | |||
</math> | </math> | ||
::<math> r=\frac{p}{1+e\cos(V)} \Longrightarrow \omega, V </math> | ::<math> r=\frac{p}{1+e\cos(V)} \Longrightarrow \omega, V \qquad \mbox{(7)}</math> | ||
::<math> \tan(E/2)=(\frac{1-e}{1+e})^{1/2}\tan(V/2) \Longrightarrow E </math> | ::<math> \tan(E/2)=(\frac{1-e}{1+e})^{1/2}\tan(V/2) \Longrightarrow E \qquad \mbox{(8)}</math> | ||
::<math> M= E -e \sin E \Longrightarrow M </math> | ::<math> M= E -e \sin E \Longrightarrow M \qquad \mbox{(9)}</math> | ||
| Line 66: | Line 69: | ||
== Calculation of the position and velocity of the satellite from its orbital elements == | == Calculation of the position and velocity of the satellite from its orbital elements == | ||
:::[[File:Osculating_Elem_Fig_1.png|none|700px]] | :::[[File:Osculating_Elem_Fig_1.png|none|700px]] (10) | ||
: where | : where | ||
:::[[File:Osculating_Elem_Fig_2.png|none|700px]] | :::[[File:Osculating_Elem_Fig_2.png|none|700px]] (11) | ||
Revision as of 14:41, 5 August 2011
| Fundamentals | |
|---|---|
| Title | Osculating Elements |
| Author(s) | J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
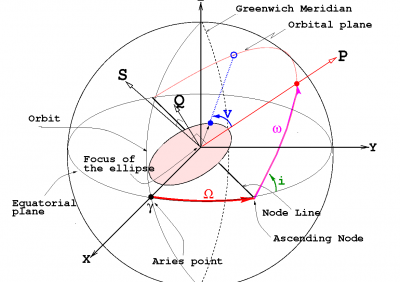
A scheme with the necessary calculations to obtain the osculating orbital elements starting from the position and velocity of the satellite, and vice-versa, is provided as follows (see figure 1):
Calculation of the orbital elements of the satellite from its position and velocity
- [math]\displaystyle{ (x, y, z, v_x, v_y, v_z) \Longrightarrow (a, e, i, \Omega, \omega, M) \qquad \mbox{(1)} }[/math]
- [math]\displaystyle{ \vec c= \vec r \times \vec v \Longrightarrow p=\frac{c^2}{\mu} \Longrightarrow p \qquad \mbox{(2)} }[/math]
- [math]\displaystyle{ v^2=\mu (2/r -1/a) \Longrightarrow a \qquad \mbox{(3)} }[/math]
- [math]\displaystyle{ p=a(1-e^2) \Longrightarrow e \qquad \mbox{(4)} }[/math]
- [math]\displaystyle{ \vec c = c \vec S \Longrightarrow \Omega=\arctan(-c_x/c_y); i=arcs(c_z/c) \Longrightarrow \Omega, i \qquad \mbox{(5)} }[/math]
- [math]\displaystyle{ \left( \begin{array}{l} x\\ y\\ z \end{array} \right) = R \left( \begin{array}{l} r \cos(V)\\ r \sin(V)\\ 0 \end{array} \right) = r \left( \begin{array}{l} \cos \Omega \cos(\omega+V)- \sin \Omega \sin(\omega+V) \cos i\\ \sin \Omega \cos(\omega+V)+ \cos \Omega \sin(\omega+V) \cos i\\ \sin(\omega+V) \sin i \end{array} \right) \Rightarrow \omega+V \qquad \mbox{(6)} }[/math]
- [math]\displaystyle{ r=\frac{p}{1+e\cos(V)} \Longrightarrow \omega, V \qquad \mbox{(7)} }[/math]
- [math]\displaystyle{ \tan(E/2)=(\frac{1-e}{1+e})^{1/2}\tan(V/2) \Longrightarrow E \qquad \mbox{(8)} }[/math]
- [math]\displaystyle{ M= E -e \sin E \Longrightarrow M \qquad \mbox{(9)} }[/math]
Calculation of the position and velocity of the satellite from its orbital elements
- (10)
- where
- (11)