If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Time References: Difference between revisions
mNo edit summary |
Paulo.Pombal (talk | contribs) |
||
| (55 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Article Infobox2 | {{Article Infobox2 | ||
|Category=Fundamentals | |Category=Fundamentals | ||
|Authors=J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. | |||
|Authors=J. Sanz Subirana, | |||
|Level=Basic | |Level=Basic | ||
|YearOfPublication=2011 | |YearOfPublication=2011 | ||
|Title={{PAGENAME}} | |||
}} | }} | ||
==Introduction== | ==Introduction== | ||
Our everyday life follows the alternation of day and night, and seasons of year, and then the initial conception of time was based on the motion of sun. Nevertheless, as science and technology evolved, more precise uniform and well-defined time scales were needed. Several time references are currently adopted, based on different periodic processes associated | Our everyday life follows the alternation of day and night, and seasons of year, and then the initial conception of time was based on the motion of sun. Nevertheless, as science and technology evolved, more precise uniform and well-defined time scales were needed. | ||
[[File:Different time systems.png|none|thumb| | |||
Several time references are currently adopted, based on the different periodic processes associated, such as earth rotation, celestial mechanics or transitions between energetic levels in atomic oscillators. Table 1 summarises the different used time systems as well their associated periodic process. | |||
: [[File:Different time systems.png|none|thumb|480px|alt=Different time systems|'''''Table 1:''''' Different time systems (from [Hofmann-Wellenhof et al., 2003]<ref> [Hofmann-Wellenhof et al., 2003 Hofmann-Wellenhof, B., Legat, K. and Wieser, M., 2003. Navigation. Principles of positioning and guidance. Springer-Verlag, Wien, Austria.</ref>)]] | |||
For information on the time references used in the different GNSS, please refer to [[Time References in GNSS]]. | |||
==Description== | |||
Universal and Sidereal times are associated with earth daily rotation. Universal time (solar time) uses the sun as a reference. Sidereal time uses the Vernal Equinox (the Aries point<ref group="footnotes">Aries point is a fictitious direction pointing to the Aries Constellation about 2000 years ago. Due to the equinox precession, Aries point is continuously moving over the ecliptic (apparent orbit of sun relative to earth) by about 50′′.26 each year, therefore in 2000 years it goes over an arc of 30° in a retrograde way. Currently, Aries point is going out of Pisces Constellation and entering Aquarius.</ref>). This leads to the fact that, in a year, both times differ by 24 hours (one lap) and, thence, the sidereal day is shorter than the solar day by 3<sup>m</sup> 56<sup>s</sup>.4, see section [[Sidereal Time]]. That is: | |||
::1 ''mean sidereal day'' = 1 ''mean solar day'' − 3<sup>m</sup>56<sup>s</sup>.4 | |||
Universal time UT (UT0, UT1, UT2) is not completely uniform<ref group="footnotes">Earth rotation is not uniform. Different phenomena as tidal friction, mass transport due to seasonal changes, earthquakes, etc. affect the earth’s mass distribution (moment of inertia), introducing fluctuations in its rotation. UT0 is a time scale based on the instantaneous rotation of the earth, UT1 is adjusted from observed periodic variations (polar motion effects, up to 0.06 seconds), and UT2 is obtained correcting it from other additional irregularities.</ref>. So, the Atomic Time TAI was introduced to achieve a more uniform time scale. TAI and UT accumulate a drift along time. Due to this, UTC was defined, which is an atomic time that keeps itself within 0.9 seconds from UT1. It is done by the systematic introduction of a certain number of seconds called ''Leap Seconds''<ref group="footnotes">From 01/01/1958 (where TAI=UTC=UT1) until November 2009, 34 seconds were added. On June 30, 2015 an additional leap second will be introduced.</ref>. This causes that, along time, the difference between UTC and TAI varies in integer leaps of 1 second. UTC is generated by the Bureau International des Poids et Mesures (BIPM), located in Paris. The leap seconds are determined by the International Earth Rotation and Reference Systems Service (IERS). | |||
UTC is obtained from about 250 cesium clocks and hydrogen masers located at about 65 different laboratories, distributed around the world, and applying a set of algorithms to assure an uniform time. It is not determined in real time, but generated with a delay of about half month. Real-time estimates of UTC are computed and provided by different centres, as the UTC(USNO), from the United States Naval Observatory (USNO), the UTC(NIST), from the National Institute of Standards and Technology (NIST), and the UTC(SU) from Russia (SU stands for the former Soviet Union) or, in general, UTC(k) as a realization of UTC by a given laboratory k, see [Lewandowski et al., 2006]<ref>[Lewandowski et al., 2006]Lewandowski, W., Matsakis, D., Panfilo, G. and Tavella, P., 2006. The evaluation of uncertainties in [UTC-UTC(k)]. Metrologia 43, pp. 278-286</ref>. ESA’s timing capability built to support the validation of the Galileo timing performances also provides an UTC estimate, formally known as UTC (ESTEC). Recently this estimate is also being providing as a contribution to the generation of the overall UTC<ref>[ http://www.esa.int/Our_Activities/Space_Engineering/ESA_s_Navigation_Lab_helps_set_global_time, ], ESA, 20 February 2013]</ref>. | |||
Please find more detailed information in [[Time Systems]]. | |||
==Time References Relationship== | |||
The following relations are met (see details in article appendix [[Transformations between Time Systems]]). | |||
::<math> | |||
\begin{array}{lcl} | \begin{array}{lcl} | ||
TAI\,=\,TDT\, | TAI\,=\,TDT\,-\,32^s.184 \\ | ||
TAI\,=\,UTC\,+\, | TAI\,=\,UTC\,+\,1^s *\,n \\ | ||
UTC\,=\,UT1\,+\,dU\, T\, 1,\, where\, |dU T 1|\, <\, | UTC\,=\,UT1\,+\,dU\, T\, 1,\, where\, |dU T 1|\, <\, 0^s.9. | ||
\end{array} | \end{array} | ||
\qquad \mbox{(1)} | |||
</math> | </math> | ||
where n is the number of Leap Seconds introduced for a given epoch (e.g., 01/Jul/97 n = 31, 01/Jan/99 n = 32, 01/Jan/06, n = 33, 01/Jan/09 n = 34). | where n is the number of Leap Seconds introduced for a given epoch (e.g., 01/Jul/97 n = 31, 01/Jan/99 n = 32, 01/Jan/06, n = 33, 01/Jan/09 n = 34). | ||
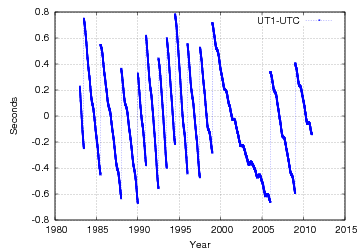
[[File:UT1-UTC and leap seconds adjustments.png|none|thumb|400px|alt=UT1-UTC and leap seconds adjustments|'''''Figure 1:''''' UT1-UTC and leap seconds adjustments]] | |||
::[[File:UT1-UTC and leap seconds adjustments.png|none|thumb|400px|alt=UT1-UTC and leap seconds adjustments|'''''Figure 1:''''' UT1-UTC and leap seconds adjustments (data from USNO)]] | |||
J2000.0 = | |||
==Calendar Systems== | |||
In order to facilitate calculations for long time intervals<ref group="footnotes">The calendar has suffered important adjustments through history, due to the fact that the length of a year is not exactly 365 days. For example, on October 5th, 1582, Pope Gregory XIII introduced a leap of 10 days –the Gregorian reform–, becoming Friday 15th. As an anecdote, Santa Teresa de Jesus died on Thursday 4th and was buried on Friday 15th, the following day – [http://www.newadvent.org/cathen/14515b.htm reference])</ref>, the Julian date is used (from Julio Scalier). The 1st of January of 4713 BC is considered as the reference epoch and, starting from there, days are counted in a correlative way. The Julian Day (JD) starts at 12<sup>h</sup> of the corresponding civil day (i.e.: 6<sup>d</sup>.0 January 1980 = JD 2444244.5). The current reference standard epoch for the scientific community is: | |||
::<math> | |||
J2000.0 = 1^d.5\, January\, 2000\, =\, JD\, 2\,451\,545.0 | |||
\qquad \mbox{(2)} | |||
</math> | </math> | ||
The Modified Julian Day (MJD) is also used, which is obtained subtracting 2 400 000.5 days from the Julian Day. The following expression provides the Julian Day from a civil date<ref group=" | |||
[[ | The Modified Julian Day (MJD) is also used, which is obtained subtracting 2 400 000.5 days from the Julian Day. | ||
From Julian Day, and taking into account that GPS reference data (6<sup>d</sup> | |||
The following expression provides the Julian Day from a civil date<ref group="footnotes">This expression is valid between March 1900 and February 2100 (year 2000 is a leap year).</ref> (YYMMDDUT): | |||
::<math> | |||
\begin{array}{ll} | |||
~~JD=int[365.25 * y]+ int[30.6001 * (m+1)] + DD +\frac{UT (hours)}{24}+1720981.5 \\[0.2cm] | |||
~\mbox{where:}\\[0.2cm] | |||
~~ \qquad y=YY-1,~~ m=MM+12,~~ MM\leq 2 & \\ | |||
~~ \qquad y=YY,~~ m=MM,~~ MM> 2\\ | |||
\end{array} | |||
\qquad \mbox{(3)} | |||
</math> | |||
From Julian Day, and taking into account that GPS reference data (6<sup>d</sup>.0 January 1980) corresponds to JD 2 444 244.5, one immediately obtains the GPST. Thence, taking module 7, the GPS week<ref group="footnotes">GPS week starts the night from Saturday to Sunday. For example, the day May 3rd, 1998 corresponded to GPS week 956.</ref> is found. | |||
The inverse transformation is given in equation (3) in [[Julian Date]]. | |||
As another example, the 3 hours (Moscow Time) on January 1st 1975 (21 hours GMT December 31st, 1974) used by GLONASS as a reference time in some computations, corresponds to JD 2 442 413.375 (GMT). | As another example, the 3 hours (Moscow Time) on January 1st 1975 (21 hours GMT December 31st, 1974) used by GLONASS as a reference time in some computations, corresponds to JD 2 442 413.375 (GMT). | ||
Greenwich Mean Sidereal (<math>\theta_{_G}</math>) Time and Universal Time are related by the following expression (see equation (4) in [[CEP to ITRF]]): | |||
::<math> | |||
\begin{array}{ll} | |||
~~\theta_{_G}=r\cdot UT1+6^h41^m50^s_{\cdot}5481+8\,640\,184^s_{\cdot}812\,866\,T_u+0^s_{\cdot}093104\,T_u^2-6^s_{\cdot}2\cdot 10^{-6}\,T_u^3\\[0.2cm] | |||
~\mbox{where:}\\[0.2cm] | |||
~~ \qquad r=1.0027379093\\ | |||
~~ \qquad T_u=(JD_{[UT1\, date]}-2\,451\,545.0)/36\,525.0\\ | |||
\end{array} | |||
\qquad \mbox{(4)} | |||
</math> | |||
==Notes== | ==Notes== | ||
<references group=" | <references group="footnotes"/> | ||
==References== | ==References== | ||
<references/> | |||
[[Category:Fundamentals]] | [[Category:Fundamentals]] | ||
[[Category:GNSS Time Reference, Coordinate Frames and Orbits]] | |||
Latest revision as of 14:42, 1 June 2015
| Fundamentals | |
|---|---|
| Title | Time References |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
Introduction
Our everyday life follows the alternation of day and night, and seasons of year, and then the initial conception of time was based on the motion of sun. Nevertheless, as science and technology evolved, more precise uniform and well-defined time scales were needed.
Several time references are currently adopted, based on the different periodic processes associated, such as earth rotation, celestial mechanics or transitions between energetic levels in atomic oscillators. Table 1 summarises the different used time systems as well their associated periodic process.
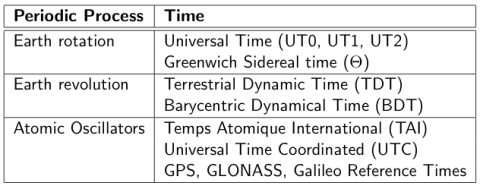 Table 1: Different time systems (from [Hofmann-Wellenhof et al., 2003][1])
Table 1: Different time systems (from [Hofmann-Wellenhof et al., 2003][1])
For information on the time references used in the different GNSS, please refer to Time References in GNSS.
Description
Universal and Sidereal times are associated with earth daily rotation. Universal time (solar time) uses the sun as a reference. Sidereal time uses the Vernal Equinox (the Aries point[footnotes 1]). This leads to the fact that, in a year, both times differ by 24 hours (one lap) and, thence, the sidereal day is shorter than the solar day by 3m 56s.4, see section Sidereal Time. That is:
- 1 mean sidereal day = 1 mean solar day − 3m56s.4
Universal time UT (UT0, UT1, UT2) is not completely uniform[footnotes 2]. So, the Atomic Time TAI was introduced to achieve a more uniform time scale. TAI and UT accumulate a drift along time. Due to this, UTC was defined, which is an atomic time that keeps itself within 0.9 seconds from UT1. It is done by the systematic introduction of a certain number of seconds called Leap Seconds[footnotes 3]. This causes that, along time, the difference between UTC and TAI varies in integer leaps of 1 second. UTC is generated by the Bureau International des Poids et Mesures (BIPM), located in Paris. The leap seconds are determined by the International Earth Rotation and Reference Systems Service (IERS).
UTC is obtained from about 250 cesium clocks and hydrogen masers located at about 65 different laboratories, distributed around the world, and applying a set of algorithms to assure an uniform time. It is not determined in real time, but generated with a delay of about half month. Real-time estimates of UTC are computed and provided by different centres, as the UTC(USNO), from the United States Naval Observatory (USNO), the UTC(NIST), from the National Institute of Standards and Technology (NIST), and the UTC(SU) from Russia (SU stands for the former Soviet Union) or, in general, UTC(k) as a realization of UTC by a given laboratory k, see [Lewandowski et al., 2006][2]. ESA’s timing capability built to support the validation of the Galileo timing performances also provides an UTC estimate, formally known as UTC (ESTEC). Recently this estimate is also being providing as a contribution to the generation of the overall UTC[3].
Please find more detailed information in Time Systems.
Time References Relationship
The following relations are met (see details in article appendix Transformations between Time Systems).
- [math]\displaystyle{ \begin{array}{lcl} TAI\,=\,TDT\,-\,32^s.184 \\ TAI\,=\,UTC\,+\,1^s *\,n \\ UTC\,=\,UT1\,+\,dU\, T\, 1,\, where\, |dU T 1|\, \lt \, 0^s.9. \end{array} \qquad \mbox{(1)} }[/math]
where n is the number of Leap Seconds introduced for a given epoch (e.g., 01/Jul/97 n = 31, 01/Jan/99 n = 32, 01/Jan/06, n = 33, 01/Jan/09 n = 34).
Calendar Systems
In order to facilitate calculations for long time intervals[footnotes 4], the Julian date is used (from Julio Scalier). The 1st of January of 4713 BC is considered as the reference epoch and, starting from there, days are counted in a correlative way. The Julian Day (JD) starts at 12h of the corresponding civil day (i.e.: 6d.0 January 1980 = JD 2444244.5). The current reference standard epoch for the scientific community is:
- [math]\displaystyle{ J2000.0 = 1^d.5\, January\, 2000\, =\, JD\, 2\,451\,545.0 \qquad \mbox{(2)} }[/math]
The Modified Julian Day (MJD) is also used, which is obtained subtracting 2 400 000.5 days from the Julian Day.
The following expression provides the Julian Day from a civil date[footnotes 5] (YYMMDDUT):
- [math]\displaystyle{ \begin{array}{ll} ~~JD=int[365.25 * y]+ int[30.6001 * (m+1)] + DD +\frac{UT (hours)}{24}+1720981.5 \\[0.2cm] ~\mbox{where:}\\[0.2cm] ~~ \qquad y=YY-1,~~ m=MM+12,~~ MM\leq 2 & \\ ~~ \qquad y=YY,~~ m=MM,~~ MM\gt 2\\ \end{array} \qquad \mbox{(3)} }[/math]
From Julian Day, and taking into account that GPS reference data (6d.0 January 1980) corresponds to JD 2 444 244.5, one immediately obtains the GPST. Thence, taking module 7, the GPS week[footnotes 6] is found.
The inverse transformation is given in equation (3) in Julian Date.
As another example, the 3 hours (Moscow Time) on January 1st 1975 (21 hours GMT December 31st, 1974) used by GLONASS as a reference time in some computations, corresponds to JD 2 442 413.375 (GMT).
Greenwich Mean Sidereal ([math]\displaystyle{ \theta_{_G} }[/math]) Time and Universal Time are related by the following expression (see equation (4) in CEP to ITRF):
- [math]\displaystyle{ \begin{array}{ll} ~~\theta_{_G}=r\cdot UT1+6^h41^m50^s_{\cdot}5481+8\,640\,184^s_{\cdot}812\,866\,T_u+0^s_{\cdot}093104\,T_u^2-6^s_{\cdot}2\cdot 10^{-6}\,T_u^3\\[0.2cm] ~\mbox{where:}\\[0.2cm] ~~ \qquad r=1.0027379093\\ ~~ \qquad T_u=(JD_{[UT1\, date]}-2\,451\,545.0)/36\,525.0\\ \end{array} \qquad \mbox{(4)} }[/math]
Notes
- ^ Aries point is a fictitious direction pointing to the Aries Constellation about 2000 years ago. Due to the equinox precession, Aries point is continuously moving over the ecliptic (apparent orbit of sun relative to earth) by about 50′′.26 each year, therefore in 2000 years it goes over an arc of 30° in a retrograde way. Currently, Aries point is going out of Pisces Constellation and entering Aquarius.
- ^ Earth rotation is not uniform. Different phenomena as tidal friction, mass transport due to seasonal changes, earthquakes, etc. affect the earth’s mass distribution (moment of inertia), introducing fluctuations in its rotation. UT0 is a time scale based on the instantaneous rotation of the earth, UT1 is adjusted from observed periodic variations (polar motion effects, up to 0.06 seconds), and UT2 is obtained correcting it from other additional irregularities.
- ^ From 01/01/1958 (where TAI=UTC=UT1) until November 2009, 34 seconds were added. On June 30, 2015 an additional leap second will be introduced.
- ^ The calendar has suffered important adjustments through history, due to the fact that the length of a year is not exactly 365 days. For example, on October 5th, 1582, Pope Gregory XIII introduced a leap of 10 days –the Gregorian reform–, becoming Friday 15th. As an anecdote, Santa Teresa de Jesus died on Thursday 4th and was buried on Friday 15th, the following day – reference)
- ^ This expression is valid between March 1900 and February 2100 (year 2000 is a leap year).
- ^ GPS week starts the night from Saturday to Sunday. For example, the day May 3rd, 1998 corresponded to GPS week 956.
References
- ^ [Hofmann-Wellenhof et al., 2003 Hofmann-Wellenhof, B., Legat, K. and Wieser, M., 2003. Navigation. Principles of positioning and guidance. Springer-Verlag, Wien, Austria.
- ^ [Lewandowski et al., 2006]Lewandowski, W., Matsakis, D., Panfilo, G. and Tavella, P., 2006. The evaluation of uncertainties in [UTC-UTC(k)]. Metrologia 43, pp. 278-286
- ^ [ http://www.esa.int/Our_Activities/Space_Engineering/ESA_s_Navigation_Lab_helps_set_global_time, ], ESA, 20 February 2013]