If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Relativistic Path Range Effect: Difference between revisions
Carlos.Lopez (talk | contribs) No edit summary |
Carlos.Lopez (talk | contribs) No edit summary |
||
| Line 34: | Line 34: | ||
==References== | ==References== | ||
[Ashby, N., 2003] Ashby, N., 2003. Relativity in the Global Positioning System. http://relativity.livingreviews.org/articles/lrr-2003-1/. | [Ashby, N., 2003] Ashby, N., 2003. Relativity in the Global Positioning System. http://relativity.livingreviews.org/articles/lrr-2003-1/. | ||
[[Category:Fundamentals]] | |||
Revision as of 10:25, 26 July 2011
| Fundamentals | |
|---|---|
| Title | Relativistic Path Range Effect |
| Author(s) | J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
This is a secondary relativistic effect that can be required only for high accuracy positioning. Its net effect on range is less than 2 cm and thence, for most
purposes it can be neglected.
This effect is named the Shapiro signal propagation delay and introduces a general relativistic correction to the geometric range: Due to the space-time curvature produced by the gravitational field, the Euclidean range computed by carrier phase measurement must be corrected by an amount given by the expression:
- [math]\displaystyle{ \rho_{_{rel}}=\frac{2\,\mu}{c^2}ln\frac{r^{sat}+r_{rcv}+r_{rcv}^{sat}}{r^{sat}+r_{rcv}-r_{rcv}^{sat}} \qquad \mbox{(1)} }[/math]
where [math]\displaystyle{ r^{sat}, r_{rcv} }[/math] are the geocentric distances of satellite and receiver and [math]\displaystyle{ r_{rcv}^{sat} }[/math] is the distance between them. The constants [math]\displaystyle{ c = 299792458 m/s }[/math] and [math]\displaystyle{ c=299792458\,m/s }[/math] and [math]\displaystyle{ \mu=G\,M_\oplus=3.986004418 \cdot 10^{14}\, m^3/s^2 }[/math] are the sped of light and the earth's gravitational constant, respectively (see GNSS Reference Frames).
This correction must be added to the Euclidian distance given by the following equation (2).
- [math]\displaystyle{ \rho_{rcv}^{sat}=\left\| {r}_{rcv}-{r}^{sat}\right \|=\sqrt{(x_{rcv}-x^{sat})^2+(y_{rcv}-y^{sat})^2+(z_{rcv}-z^{sat})^2} \qquad \mbox{(2)} }[/math]
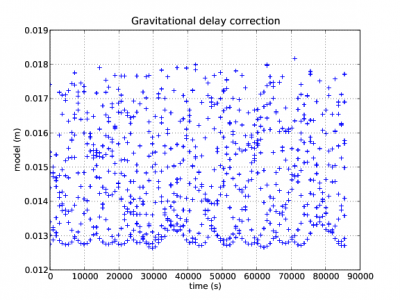
Next figure 1 illustrates with an example the Shapiro signal propagation delays for the satellites in view from a receiver in Barcelona, Spain (receiver coordinates [math]\displaystyle{ \lambda\simeq 2^ o $\phi \simeq 41^o }[/math]).
A very good review of relativistic effects on GPS can be found in [Ashby, N., 2003], (see http://relativity.livingreviews.org/Articles/lrr-2003-1).
References
[Ashby, N., 2003] Ashby, N., 2003. Relativity in the Global Positioning System. http://relativity.livingreviews.org/articles/lrr-2003-1/.