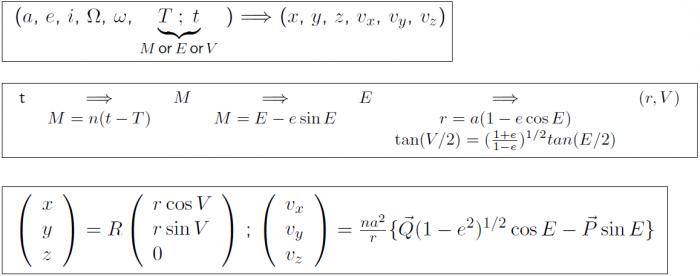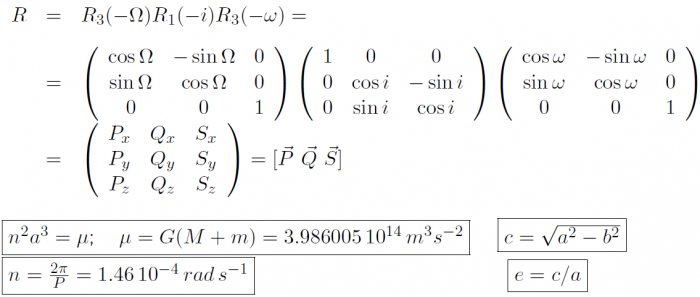If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
APPROVED
Not Approved
Vicente.Navarro approved this page 14 July 2025
14 July 2025
Osculating Elements: Difference between revisions
Jump to navigation
Jump to search
Carlos.Lopez (talk | contribs) (Created page with "{{Article Infobox2 |Category=Fundamentals |Title={{PAGENAME}} |Authors= J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain. |Level=Medium...") |
Jaume.Sanz (talk | contribs) No edit summary |
||
| (6 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Article Infobox2 | {{Article Infobox2 | ||
|Category=Fundamentals | |Category=Fundamentals | ||
|Authors=J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. | |||
|Level=Advanced | |||
|YearOfPublication=2011 | |||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
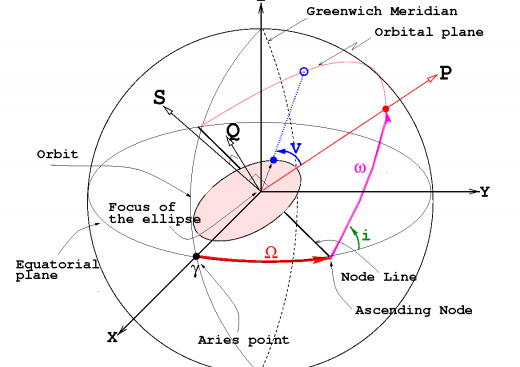
A scheme with the necessary calculations to obtain the osculating orbital elements starting from the position and velocity of a satellite in a geocentric inertial system, and vice-versa, is provided as follows (see figure 1): | |||
== Calculation of the orbital elements of the satellite from its position and velocity == | |||
::<math> (x, y, z, v_x, v_y, v_z) \Longrightarrow (a, e, i, \Omega, \omega, M) \qquad \mbox{(1)}</math> | |||
== | ::<math> \vec c= \vec r \times \vec v \Longrightarrow p=\frac{c^2}{\mu} \Longrightarrow p \qquad \mbox{(2)}</math> | ||
::<math> v^2=\mu (2/r -1/a) \Longrightarrow a \qquad \mbox{(3)}</math> | |||
::<math> ( | ::<math> p=a(1-e^2) \Longrightarrow e \qquad \mbox{(4)}</math> | ||
::<math> \vec c = c \vec S \Longrightarrow \Omega=\arctan(-c_x/c_y); i=arcs(c_z/c) \Longrightarrow \Omega, i \qquad \mbox{(5)}</math> | |||
::<math> \vec c = c \vec S \Longrightarrow \Omega=\arctan(-c_x/c_y); i=arcs(c_z/c) \Longrightarrow \Omega, i </math> | |||
| Line 48: | Line 48: | ||
\end{array} | \end{array} | ||
\right) | \right) | ||
\Rightarrow \omega+V | \Rightarrow \omega+V | ||
\qquad \mbox{(6)} | |||
</math> | </math> | ||
::<math> r=\frac{p}{1+e\cos(V)} \Longrightarrow \omega, V </math> | ::<math> r=\frac{p}{1+e\cos(V)} \Longrightarrow \omega, V \qquad \mbox{(7)}</math> | ||
::<math> \tan(E/2)=(\frac{1-e}{1+e})^{1/2}\tan(V/2) \Longrightarrow E </math> | ::<math> \tan(E/2)=(\frac{1-e}{1+e})^{1/2}\tan(V/2) \Longrightarrow E \qquad \mbox{(8)}</math> | ||
::<math> M= E -e \sin E \Longrightarrow M </math> | ::<math> M= E -e \sin E \Longrightarrow M \qquad \mbox{(9)}</math> | ||
| Line 66: | Line 66: | ||
== Calculation of the position and velocity of the satellite from its orbital elements == | == Calculation of the position and velocity of the satellite from its orbital elements == | ||
:::[[File:Osculating_Elem_Fig_1.png|none|700px]] | :::[[File:Osculating_Elem_Fig_1.png|none|700px]] (10) | ||
: where | : where | ||
:::[[File:Osculating_Elem_Fig_2.png|none|700px]] | :::[[File:Osculating_Elem_Fig_2.png|none|700px]] (11) | ||
:::[[File:Osculating_Elem_Fig_3.png|none|thumb| | :::[[File:Osculating_Elem_Fig_3.png|none|thumb|520px|'''''Figure 1:''''' Orbit in space.]] | ||
[[Category:Fundamentals]] | [[Category:Fundamentals]] | ||
[[Category:GNSS Measurements and Data Preprocessing]] | |||
Latest revision as of 10:34, 13 January 2013
| Fundamentals | |
|---|---|
| Title | Osculating Elements |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
A scheme with the necessary calculations to obtain the osculating orbital elements starting from the position and velocity of a satellite in a geocentric inertial system, and vice-versa, is provided as follows (see figure 1):
Calculation of the orbital elements of the satellite from its position and velocity
- [math]\displaystyle{ (x, y, z, v_x, v_y, v_z) \Longrightarrow (a, e, i, \Omega, \omega, M) \qquad \mbox{(1)} }[/math]
- [math]\displaystyle{ \vec c= \vec r \times \vec v \Longrightarrow p=\frac{c^2}{\mu} \Longrightarrow p \qquad \mbox{(2)} }[/math]
- [math]\displaystyle{ v^2=\mu (2/r -1/a) \Longrightarrow a \qquad \mbox{(3)} }[/math]
- [math]\displaystyle{ p=a(1-e^2) \Longrightarrow e \qquad \mbox{(4)} }[/math]
- [math]\displaystyle{ \vec c = c \vec S \Longrightarrow \Omega=\arctan(-c_x/c_y); i=arcs(c_z/c) \Longrightarrow \Omega, i \qquad \mbox{(5)} }[/math]
- [math]\displaystyle{ \left( \begin{array}{l} x\\ y\\ z \end{array} \right) = R \left( \begin{array}{l} r \cos(V)\\ r \sin(V)\\ 0 \end{array} \right) = r \left( \begin{array}{l} \cos \Omega \cos(\omega+V)- \sin \Omega \sin(\omega+V) \cos i\\ \sin \Omega \cos(\omega+V)+ \cos \Omega \sin(\omega+V) \cos i\\ \sin(\omega+V) \sin i \end{array} \right) \Rightarrow \omega+V \qquad \mbox{(6)} }[/math]
- [math]\displaystyle{ r=\frac{p}{1+e\cos(V)} \Longrightarrow \omega, V \qquad \mbox{(7)} }[/math]
- [math]\displaystyle{ \tan(E/2)=(\frac{1-e}{1+e})^{1/2}\tan(V/2) \Longrightarrow E \qquad \mbox{(8)} }[/math]
- [math]\displaystyle{ M= E -e \sin E \Longrightarrow M \qquad \mbox{(9)} }[/math]
Calculation of the position and velocity of the satellite from its orbital elements
- (10)
- where
- (11)