If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Klobuchar Ionospheric Model: Difference between revisions
Jaume.Sanz (talk | contribs) No edit summary |
Carlos.Lopez (talk | contribs) No edit summary |
||
| (8 intermediate revisions by one other user not shown) | |||
| Line 4: | Line 4: | ||
|Level=Advanced | |Level=Advanced | ||
|YearOfPublication=2011 | |YearOfPublication=2011 | ||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
GPS satellites broadcast the parameters of the Klobuchar ionospheric model for single frequency users. The Klobuchar model was designed to minimise user computational complexity and user computer storage as far as to keep a minimum number of coefficients to transmit on satellite-user link. | GPS satellites broadcast the parameters of the Klobuchar ionospheric model for single frequency users. The Klobuchar model was designed to minimise user computational complexity and user computer storage as far as to keep a minimum number of coefficients to transmit on satellite-user link. | ||
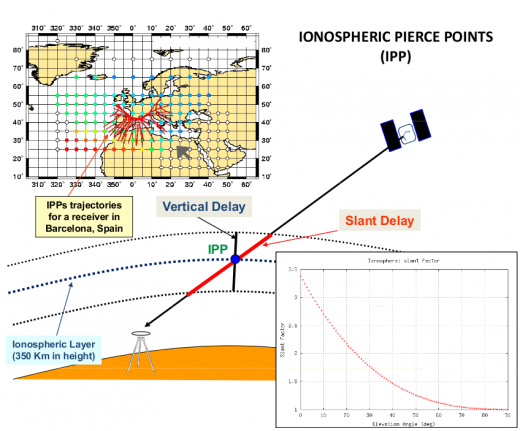
This broadcast model is based on an empirical approach <ref name="Klobuchar"> [Klobuchar, 1987] Klobuchar, J., 1987. Ionospheric Time-Delay Algorithms for Single-Frequency GPS Users. IEEE Transactions on Aerospace and Electronic Systems (3), pp. 325 | This broadcast model is based on an empirical approach [Klobuchar, 1987] <ref name="Klobuchar"> [Klobuchar, 1987] Klobuchar, J., 1987. Ionospheric Time-Delay Algorithms for Single-Frequency GPS Users. IEEE Transactions on Aerospace and Electronic Systems (3), pp. 325-331.</ref> and is estimated to reduce about the 50% RMS ionospheric range error worldwide. It is assumed that the electron content is concentrated in a thin layer at <math>350</math> kilometres in height. Thence, the slant delay is computed from the vertical delay at the Ionospheric Pierce Point (IPP) <ref group="footnotes">That is the intersection of the ray with the ionospheric layer at <math>350</math> kilometres in height.</ref> multiplying by a obliquity factor, i.e., the mapping function, see figure 1 and equation (9). | ||
| Line 17: | Line 16: | ||
'''''Klobuchar Algorithm equations''''' | '''''Klobuchar Algorithm equations''''' | ||
The Klobuchar algorithm to run in a single frequency receiver is provided as follows (from <ref name="Klobuchar"/>): | The Klobuchar algorithm to run in a single frequency receiver is provided as follows (from [Klobuchar, 1987]<ref name="Klobuchar"/>): | ||
Given the user approximate geodetic latitude <math>\phi_u</math>, longitude <math>\lambda_u</math>, elevation angle <math>E</math> and azimuth <math>A</math> of the observed satellite and the coefficients <math>\alpha_n</math> and <math>\beta_n</math> broadcasted in the GPS satellite navigation message: | Given the user approximate geodetic latitude <math>\displaystyle \phi_u</math>, longitude <math>\displaystyle \lambda_u</math>, elevation angle <math>\displaystyle E</math> and azimuth <math>\displaystyle A</math> of the observed satellite and the coefficients <math>\displaystyle \alpha_n</math> and <math>\displaystyle \beta_n</math> broadcasted in the GPS satellite navigation message: | ||
:'''1. Calculate the earth-centred angle (elevation <math>E</math> in semicircles).''' | :'''1. Calculate the earth-centred angle (elevation <math>\displaystyle E</math> in semicircles).''' | ||
::<math> | ::<math> | ||
| Line 35: | Line 34: | ||
:If <math>\ | :If <math>\displaystyle \Phi_I> +0.416</math> the <math>\displaystyle \Phi_I=+0.416</math>. If <math>\Phi_I< -0.416</math> the <math>\Phi_I=-0.416</math>. | ||
| Line 119: | Line 118: | ||
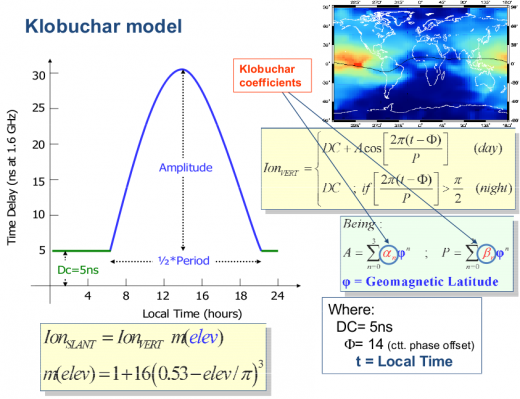
Figure 2 is a layout of the Klobuchar model algorithm, showing that the vertical delays are based on a constant value at night time and a half-cosine function in daytime, which amplitude and period | Figure 2 is a layout of the Klobuchar model algorithm, showing that the vertical delays are based on a constant value at night time and a half-cosine function in daytime, which amplitude and period are given as a function of the eight parameters (<math>\alpha_i,\, \beta_i,\,i=0,\dots,3</math>) broadcast in the GPS navigation message. A map with the geographical variation of the vertical delay is also depicted in this figure. | ||
Latest revision as of 11:34, 23 February 2012
| Fundamentals | |
|---|---|
| Title | Klobuchar Ionospheric Model |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
GPS satellites broadcast the parameters of the Klobuchar ionospheric model for single frequency users. The Klobuchar model was designed to minimise user computational complexity and user computer storage as far as to keep a minimum number of coefficients to transmit on satellite-user link.
This broadcast model is based on an empirical approach [Klobuchar, 1987] [1] and is estimated to reduce about the 50% RMS ionospheric range error worldwide. It is assumed that the electron content is concentrated in a thin layer at [math]\displaystyle{ 350 }[/math] kilometres in height. Thence, the slant delay is computed from the vertical delay at the Ionospheric Pierce Point (IPP) [footnotes 1] multiplying by a obliquity factor, i.e., the mapping function, see figure 1 and equation (9).
Klobuchar Algorithm equations
The Klobuchar algorithm to run in a single frequency receiver is provided as follows (from [Klobuchar, 1987][1]):
Given the user approximate geodetic latitude [math]\displaystyle{ \displaystyle \phi_u }[/math], longitude [math]\displaystyle{ \displaystyle \lambda_u }[/math], elevation angle [math]\displaystyle{ \displaystyle E }[/math] and azimuth [math]\displaystyle{ \displaystyle A }[/math] of the observed satellite and the coefficients [math]\displaystyle{ \displaystyle \alpha_n }[/math] and [math]\displaystyle{ \displaystyle \beta_n }[/math] broadcasted in the GPS satellite navigation message:
- 1. Calculate the earth-centred angle (elevation [math]\displaystyle{ \displaystyle E }[/math] in semicircles).
- [math]\displaystyle{ \psi =\frac{0.0137}{E+0.11}-0.022 \qquad\mbox{(semicircles)} \qquad\mbox{(1)} }[/math]
- 2. Compute the latitude of the Ionospheric Pierce Point (IPP)[footnotes 2].
- [math]\displaystyle{ \phi_I=\phi_u+\psi \cos A \qquad\mbox{(semicircles)} \qquad\mbox{(2)} }[/math]
- If [math]\displaystyle{ \displaystyle \Phi_I\gt +0.416 }[/math] the [math]\displaystyle{ \displaystyle \Phi_I=+0.416 }[/math]. If [math]\displaystyle{ \Phi_I\lt -0.416 }[/math] the [math]\displaystyle{ \Phi_I=-0.416 }[/math].
- 3. Compute the longitude of the IPP.
- [math]\displaystyle{ \lambda_I=\lambda_u+\frac{\psi \sin A}{\cos \phi_I} \qquad\mbox{(semicircles)} \qquad\mbox{(3)} }[/math]
- 4. Find the geomagnetic latitude of the IPP.
- [math]\displaystyle{ \phi_m=\phi_I+0.064 \, \cos (\lambda_I-1.617) \qquad\mbox{(semicircles)} \qquad\mbox{(4)} }[/math]
- 5. Find the local time at the IPP.
- [math]\displaystyle{ t= 43\,200\, \lambda_I + t_{GPS}\mbox{(seconds)} \qquad\mbox{(5)} }[/math]
- where [math]\displaystyle{ \leq t \lt 86\,400 }[/math],
- therefore: If [math]\displaystyle{ t\geq 86\,400 }[/math], subtract [math]\displaystyle{ 86\,400 }[/math]. If [math]\displaystyle{ t\lt 0 }[/math], add [math]\displaystyle{ 86\,400 }[/math].
- 6. Compute the amplitude of ionospheric delay.
- [math]\displaystyle{ A_I=\displaystyle\sum_{n=0}^{3}{\alpha_n \phi_m^n} \qquad\mbox{(seconds)} \qquad\mbox{(6)} }[/math]
- if [math]\displaystyle{ A_I\lt 0 }[/math], thence [math]\displaystyle{ A_I=0 }[/math].
- 7. Compute the period of ionospheric delay.
- [math]\displaystyle{ P_I=\displaystyle\sum_{n=0}^{3}{\beta_n \phi_m^n}\qquad\mbox{(seconds)} \qquad\mbox{(7)} }[/math]
- if [math]\displaystyle{ P_I\lt 72\,000 }[/math], thence [math]\displaystyle{ P_I=72\,000 }[/math].
- 8. Compute the phase of ionospheric delay.
- [math]\displaystyle{ X_I=\displaystyle \frac{\displaystyle 2\pi(t-50\,400)}{P_I} \qquad\mbox{(radians)} \qquad\mbox{(8)} }[/math]
- 9. Compute the slant factor (elevation [math]\displaystyle{ E }[/math] in semicircles).
- [math]\displaystyle{ F=1.0+16.0\,(0.53-E)^3 \qquad\mbox{(9)} }[/math]
- 10. Compute the ionospheric time delay.
- [math]\displaystyle{ I_{_{_{L1_{GPS}}}}=\left \{ \begin{array}{ll} \left [5\cdot 10^{-9}+ \sum_{n=0}^{3}{\alpha_n \phi_m^n}\cdot \left ( 1- \frac{X_I^2}{2}+\frac{X_I^4}{24} \right) \right ] \cdot F &; |X_I|\leq 1.57\\[0.5cm] 5\cdot 10^{-9}\cdot F &; |X_I|\geq 1.57 \end{array} \right . \qquad\mbox{(10)} }[/math]
- The delay [math]\displaystyle{ I_{_{L1_{GPS}}} }[/math] is given in seconds and it is referred to the GPS L1 frequency.
- Note: For the L1 GPS signal, the delay [math]\displaystyle{ I_{_{L1_{GPS}}} }[/math] corresponds to the term [math]\displaystyle{ \hat{\alpha}_1\,I }[/math] in
- [math]\displaystyle{ \begin{array}{l} R_{_1}=\rho+c(\delta t_{rcv}-\delta t^{sat})+T+\tilde{\alpha_1}(I+K_{21})+\mathcal{M}_1+\varepsilon_1\\[0.2cm] \Phi_{_1}=\rho+c(\delta t_{rcv}-\delta t^{sat})+T- \tilde{\alpha_1}(I+K_{21})+b_1+\lambda_1\,N_1+\lambda_1 w+m_1+\epsilon_1 \end{array} \qquad\mbox{(11)} }[/math]
Although this algorithm is provided to estimate the ionospheric delay in the GPS L1 frequency signal, it can be also used to estimate the ionospheric time delay in the GPS L2 frequency signal or for the GLONASS and Galileo signals, as well. Indeed, taking into account that the ionospheric delay is inversely proportional to the square of the signal frequency, the delay for any GNSS signal transmitted on frequency [math]\displaystyle{ f }[/math] is given by:
- [math]\displaystyle{ I_f= \left ( \frac{f_{_{L1_{GPS}}}}{f} \right )^2\,I_{_{L1_{GPS}}} \qquad\mbox{(12)} }[/math]
Figure 2 is a layout of the Klobuchar model algorithm, showing that the vertical delays are based on a constant value at night time and a half-cosine function in daytime, which amplitude and period are given as a function of the eight parameters ([math]\displaystyle{ \alpha_i,\, \beta_i,\,i=0,\dots,3 }[/math]) broadcast in the GPS navigation message. A map with the geographical variation of the vertical delay is also depicted in this figure.
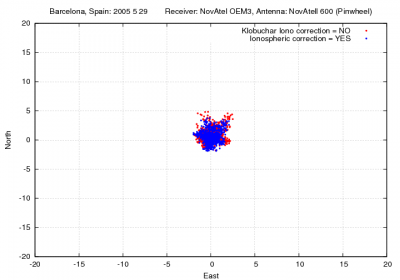
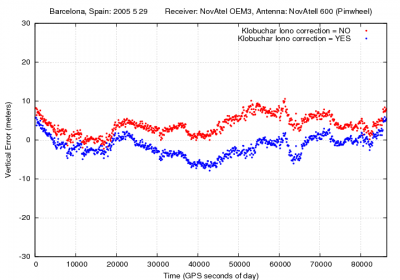
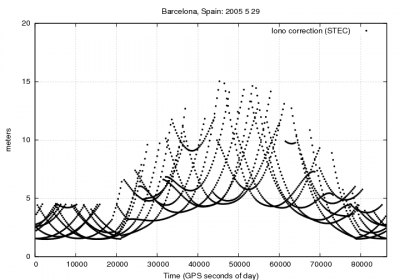
Figure 3 illustrates with an example the values of the GPS delays from the Klobuchar model and shows the effect of neglecting such delays in single point positioning for the horizontal and vertical error components.
Figure 3: Ionospheric correction: Range and position domain effect First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the Klobuchar ionospheric correction defined in 1. The variation in range is shown in the second row at left
Notes