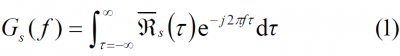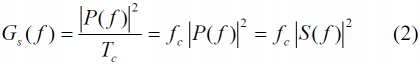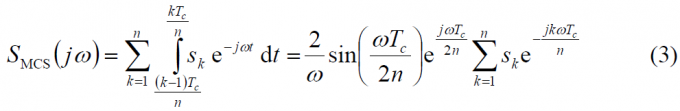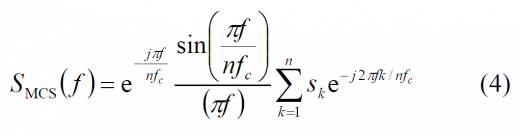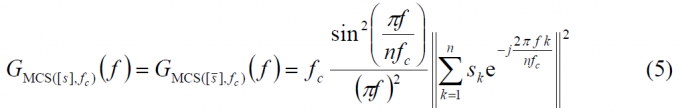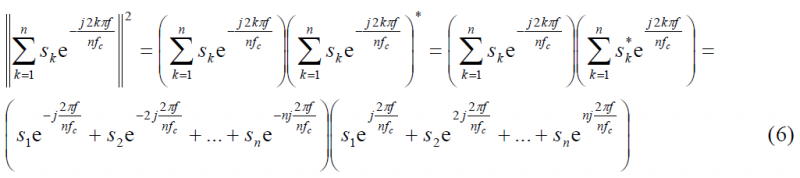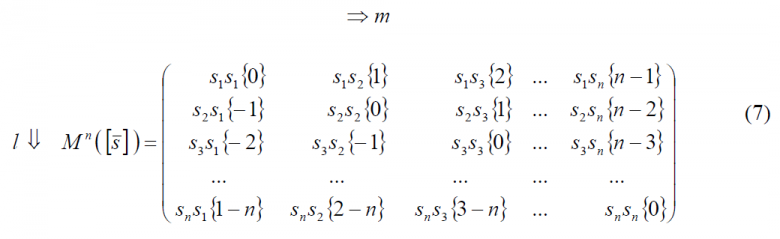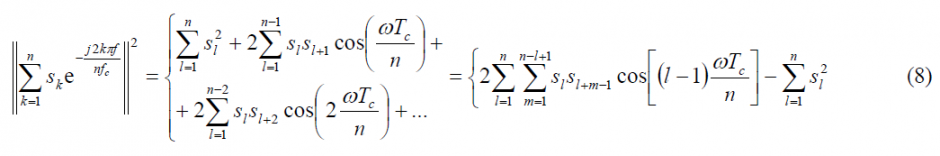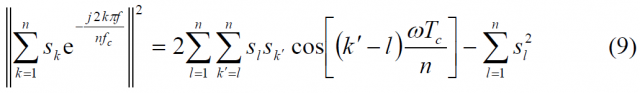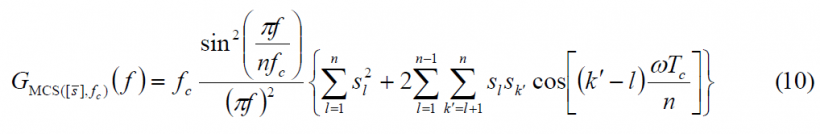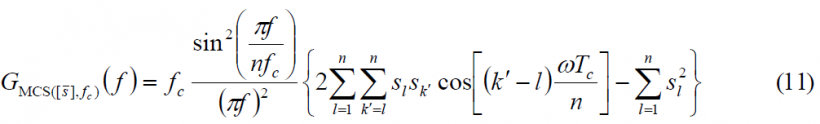If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Multilevel Coded Spreading Symbols (MCS)
| Fundamentals | |
|---|---|
| Title | Multilevel Coded Spreading Symbols (MCS) |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
Generalizing the definition of [J.W. Betz, 2003] [1], [C.J. Hegarty, 2003][2] and [A.R. Pratt and J.I.R. Owen, 2003b][3] to non-binary signals, Multilevel Coded Spreading Symbols can be seen as generalizations of BPSK and BOC. Each spreading symbol (which is phase modulated by a spreading code value) is divided into a number of equal-length segments, each of which is assigned a deterministic value. As we can infere from this definition, each of the segments, also called subchips, can in principle adopt any value. The shape of the subchip could be thus rectangular, sinusoidal or something different.
The notation we will follow to define an MCS signal is [math]\displaystyle{ MCS([s], fc) }[/math] where [s] represents the MCS sequence in one chip and fc is the chip rate.
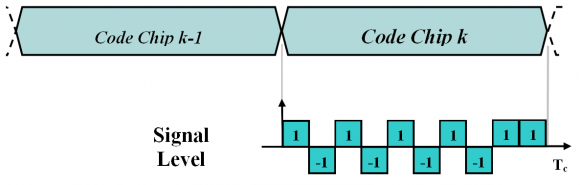
As shown in [C.J. Hegarty et al., 2005] [4] and [C.J. Hegarty et al., 2004] [5], Binary Coded Symbols are already present in the literature since long time ago but it has not been until recent times that they have been considered as a serious alternative to the current BPSK and BOC modulations. In fact, the BPSK modulation can also be denoted as [math]\displaystyle{ BCS([1], fc) }[/math] having each segment unit value all over the chip. In a similar way, [math]\displaystyle{ BOC(1,1) }[/math] has fs=1 and fc=1 and thus a BCS sequence with values [+1,-1] spread with a 1.023 MHz code would uniquely define it. According to our definition, [math]\displaystyle{ BOC(1,1) }[/math] can also be denoted as [math]\displaystyle{ BCS([1,-1],1) }[/math]. The following figure shows how a particular BCS signal could look like.
We can go one step further in our definition of Binary Coded Symbols in line with [J.W. Betz, 2003] [1] and define [math]\displaystyle{ BCS([s1],[s2],…,[sn], fc) }[/math] as the result of blending n different binary coded symbols at a chip rate fc. This can be achieved for example by time multiplexing the different spreading symbols or by using different BCS sequences on In-phase and quadrature phase channels with independent spreading channels. The MBOC signal relies on this blending concept. In the same manner [math]\displaystyle{ MCS([s1],[s2],…,[sn], fc) }[/math] would be the result of blending n different Multilevel coded symbols at a chip rate fc.
Binary Coded Symbols have gained in interest for the enormous flexibility that they could offer for future GNSS optimizations.
MCS sequences are a promising field since well selected configurations offer clear performance advantages as well as the possibility to control spectral properties in a more efficient way. This aspect has been of crucial importance during the design of Galileo in order to be compatible and interoperable with GPS, and could show us the way to proceed in the future when new signals are planned to be placed in the already crowded RNSS bands.
MCS Power Spectral Density
The power spectrum of any DSSS signal can be obtained by means of its corresponding autocorrelation function:
or by means of the Fourier Transform of the signal,
For the sake of convenience we will use the notation to refer to the chip waveform spectrum. In the following lines, we will make use of this latter expression to derive the PSD of a generic MCS signal. Indeed, the Fourier transform of a generic signal MCS([s], fc) is shown to be:
where n refers to the number of symbols in one chip and fc is the chip rate of the MCS signal.
This can be further expressed in the frequency domain as follows:
Once we have a general expression for the Fourier transform of an MCS signal, the power spectral density can be derived according to [math]\displaystyle{ G_s(f)=\frac{{\left |P(f) \right |}^2}{T_c}=f_c {\left | P(f) \right |}^2 }[/math] (refer to Autocorrelation & Power Spectral Density) as follows:
We can go one step further in our derivation if we assume that the sequence consists of real coefficients (not necessarily binary) such that ,[math]\displaystyle{ s_k = s_k^* }[/math]. In this case,
For simplicity in the notation we call [math]\displaystyle{ e^{jk \frac {2 \pi f}{n f_c}}=\left \{k \right \} }[/math] and we will express the product of sums of (6) by means of the following matrix representation:
where l denotes the row index and m the column index. Since the coefficients are assumed to be real, [math]\displaystyle{ s_l s_m^* = s_l^* s_m=s_l s_m }[/math] and the sum of all the terms in the matrix above can be expressed as follows:
Furthermore, we can express the term in parentheses in a more simplified form if we apply the variable change l+m-1=k’, yielding thus:
Observing the matrix of (7) above, we can clearly see that we only need to look at the terms of the right superior triangular part of the matrix to compute the PSD of the MCS signal for any given real sequence. Moreover, it must be noted again that this sequence has not to be necessarily binary, being BCS a particular case of MCS as defined in the lines above. Combining now (5) and (9) we have the general expression for the power spectral density of a generic MCS signal:
or equivalently,
References
- ^ a b [J.W. Betz, 2003] J.W. Betz, Brief Overview of Binary and Quadraphase Coded Symbols for GNSS, 2 December 2003, Updated 18 December 2003.
- ^ [C.J. Hegarty, 2003] C.J. Hegarty, Alternative Bi-phase GNSS Modulations, MITRE Memo F82-M04-004, 24 November 2003.
- ^ [A.R. Pratt and J.I.R. Owen, 2003b] A.R. Pratt and J.I.R. Owen, Performance of GPS Galileo Receivers Using m-PSK BOC Signals, Proceedings of the International Technical Meeting of the Institute of Navigation, ION-GNSS 2003, 9-12 September 2003, Portland, Oregon, USA.
- ^ [C.J. Hegarty et al., 2005] C.J. Hegarty, J.W. Betz and A. Saidi, Binary Coded Symbol Modulations for GNSS, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 2005, January 2005, San Diego, California, USA.
- ^ [C.J. Hegarty et al., 2004] C.J. Hegarty, M. Tran and J.W. Betz, Multipath Performance of the new GNSS Signals, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 2004, January 2004, San Diego, California, USA.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)