If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
The Stanford – ESA Integrity Diagram: Focusing on SBAS Integrity
| EGNOS | |
|---|---|
| Title | The Stanford – ESA Integrity Diagram: Focusing on SBAS Integrity |
| Author(s) | M. Tossaint, J. Samson, F. Toran and J. Ventura-Traveset, European Space Agency, ESA; J. Sanz, M. Hernandez-Pajares and J.M. Juan, UPC, Barcelona, Spain; A. Tadjine and I. Delgado, GMV, Spain. |
| Level | Advanced |
| Year of Publication | 2006 |
Abstract
In this article, a new concept for SBAS integrity validation is presented. The proposed concept is a modification of the well-known Stanford diagram[1], where a 2D histogram shows the relationship of position errors against protection levels for a set of measurements using an all in view satellite selection. The new method consists on two diagrams: the Worst-Safety Index diagram and the “All-Geometries” diagram, known here as the Stanford-ESA and the All-Stanford-ESA, respectively. The first consist on taking, at each sample time and given location, the worst possible satellite geometrical combination (out of all possible combinations) from a SBAS integrity margin viewpoint. In the second, all possible geometries are displayed and, in case of MIs, the geometries associated to each epoch are leveled with different symbols and colors. It allows, to easily identify the different clusters and to assess the time correlation of the events. Real measurement results are presented here showing that the EGNOS integrity margins remain safe under this very exigent criterion, a certainly very positive result.
Introduction
The Satellite Based Augmentation Systems (SBAS) broadcast through GEO satellites GPS-like navigation signals containing differential corrections and integrity data to enhance the GNSS positioning and making it suitable for safety critical applications such as civil aviation.
Integrity is the system’s ability to provide warnings to the user when the system is not available for a specific operation. The SBAS systems provides the users with integrity information to compute the Protection Levels (Horizontal and Vertical protection levels HPL and VPL), which represent an upper bound of the error. For each operational mode, Alert Limits (AL) against which the user has to compare its Protection Levels are defined (ICAO’s GNSS SARPS)[2], and the system is declared Unavailable when the Protection Level is greater than the Alert Limit. If the system is available and the Position Error is not bounded by the Protection Level, thence the event is considered as a Misleading Information (MI), since the Protection Level is always supposed to be an upper bound of the Position Error. Moreover, the event is declared as Hazardously Misleading Information (HMI) if the Position Error exceeds the AL (see Figure 1).
The Stanford Plot has become a reference representation technique in the SBAS domain, especially to have a quick and clear view of system performances, highlighting its capability to clearly show the integrity margins offered by SBAS. This Diagram uses an all-in-view approach (i.e. all GPS satellites in view with valid differential corrections available) for computing the error/protection level pair (XPE,XPL) to plot for each time sample. For further details on the Stanford Plot, the reading of [1] is highly recommended.
When focusing on integrity, though, the classical Stanford Plot is not always conservative. Indeed, using all in view satellites to measure integrity over-bounding capability may lead, for instance, to a situation in which a specific integrity loss in one or more satellite may be mitigated by other “well-bounded” line of sight, so that the net effect at position domain would not be appreciated. Furthermore, there is no obligation for the users to use always all available satellites, since for instance in some cases, some satellites in view may have been discarded because of a wrong tracking. Those users may have big discrepancies in performances with respect to others.
To overcome the above limitations, a new concept for SBAS integrity validation is presented in this work, consisting of a modification of the Stanford Plot. ESA detailed studies on the transfer of integrity between pseudo-range and position domains[3], have led to the introduction of a specific kind of representation technique able to provide a strong evidence of the robustness of an SBAS (Satellite Based Augmentation System) system with respect to integrity bound provision, and for all possible satellite geometrical conditions. This new representation is then exclusively focussed on Integrity (versus the Integrity, Availability, and Accuracy information of the bi-dimensional nominal Stanford Diagram).
During the SBAS Interoperability Working Group meeting celebrated in Madrid (Spain) in March 2005, it was suggested to call this new Integrity representation as the “Stanford-ESA Integrity Diagram”.
The Stanford-ESA integrity diagram has been included in the GNSS Supervisory Authority (GSA) recommendations for the EGNOS safety certification as a main tool for the integrity assessment in the position domain.
The Stanford-ESA Modified Integrity Diagram
The Stanford-ESA Integrity Diagram, as the name itself indicates, is a modification of the well-known Integrity-Availability-Accuracy 2D histogram proposed by the WAAS laboratory of the Stanford University, commonly known as “Stanford Plot”. This new Integrity Diagram concept proposes exactly the same representation technique, but introducing a modification in the data to be used as input source to build the graph, which focuses exclusively on integrity.
The “all geometries” Stanford-ESA Integrity Diagram
Instead of representing each (XPE, XPL) pair for an all-in-view situation, it does that, at every second, for all the combinations of satellites from 4 to all-in-view. Moreover, the right of diagonal is modified as follows:
- If a MI happens, all the geometries on the right of diagonal are plotted with the same colour, and with a common symbol (square, star, triangle,…). And the colour indicates the epoch relative to the time interval recorded in the file, in the colour bar of the plot.
- The previous rule applies only to the last 10 epochs with MIs. All the other epochs with MIs (if it happens) will be display as in the left side. Nevertheless, this situation should be extremely rare and will indicate an important anomaly from the receiver or system.
The aim of previous rules is to identify the sets of geometries associated to the same MI and, especially, to provide some information about the time correlation of such MIs. In this way, the all-geometries diagram provides a quick and clear view of the system performance for the all possible geometries (not only for all-in-view). And, at the same time, the display is enhanced with time information for the unsafe geometries (i.e., with MIs), which are clustered by epochs using different symbols. Finally, at the bottom of the plot it is written the “number of epochs and geometries with XPE>XPL”, which summarizes the simple pass/fail criterion: no points on the right of diagonal (for any geometry at any epoch).
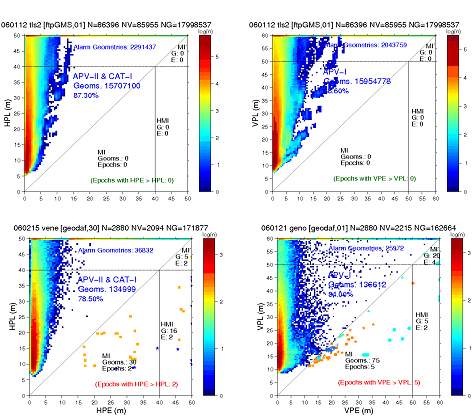
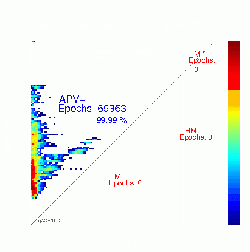
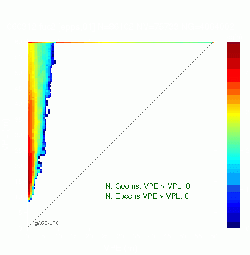
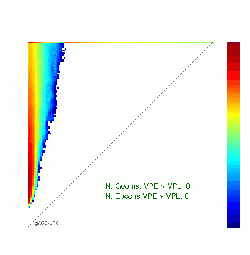
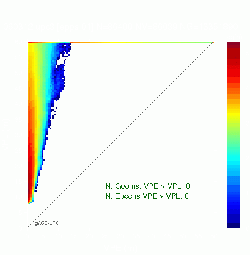
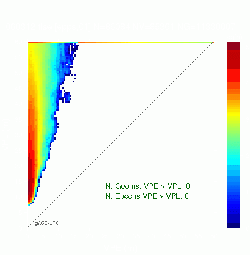
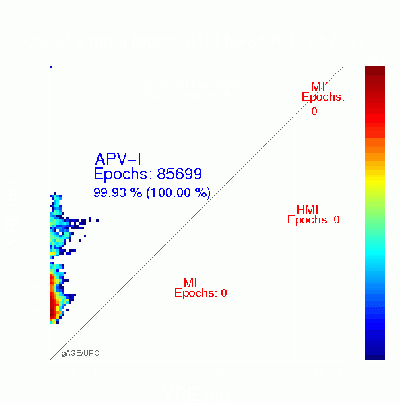
Four examples of all geometries diagrams are given in Figure 2. The first row shows two examples of diagram without MIs. Notice that, although the figure at left has no MIs, the pattern is quite disperse, with several points close to the diagonal. The figure at right shows the expected performance for a safety system.
The diagrams of second row do not fulfill the integrity criteria, having geometries with MIs. In the left side diagram only two epochs are involved, labeled by blue-stars and red-squares. Such epochs are far in time. The first epoch (dark blue-stars) corresponds to the beginning of the file. The second one (red-squares) happened at the end of data collecting period. Thence, such MIs are independent in time. The figure at bottom right shows a diagram with several geometries having MIs which involve four epochs. The MIs happen basically in three different periods of times: At the beginning of the file (dark blue-circles), at the middle (light green stars and triangles) and at the end of file (red squares). Notice that the epochs labeled with stars and triangles are very close in time (booth have the same color).
The idea of considering all possible subsets of satellites is not new, it is widely used in Receiver Autonomous Integrity Monitoring (RAIM) for satellite fault detection and exclusion [4]: The receiver explores all the combinations of n satellites in view (n>4, for detection and n>5 for exclusion) where n is the number of satellites range measurements used in the position solution. For each subset of satellites, it performs a least square solution of position and clock offset based on pseudorange measurements to the chosen satellites. A statistic test for fault detection is then derived as a function of the range residuals.
Other example is the Position Domain Monitoring (PDM) concept introduced in Local Area Augmentation System (LAAS) [5], where a remote receiver hosting the PDM derives position solutions using all visible satellites (approved by the LAAS Ground Facility) and all reasonable subsets of these satellites. These position solutions are compared to the known (surveyed) PDM antenna, and errors exceeding the detection threshold are alerted.
In our case, the target is not to exclude the faulty satellites or to warn the users in a real time monitoring. The target is to have a tool to perform a strong SBAS Position Domain Integrity Validation, in such a way that, if no over-bounding is detected for any geometry at the user level, thence it can be assured that the integrity margins are safe. This cannot be fully assessed with the classical Stanford plot, as it is shown in next Figures 3 and 4:
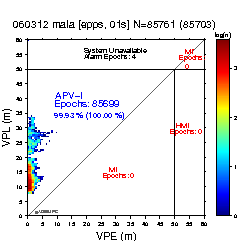
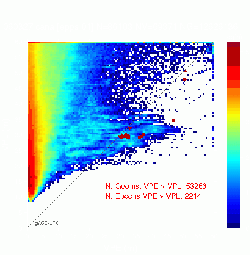
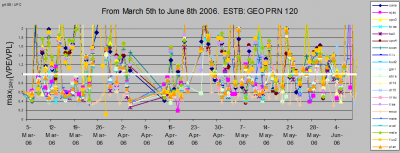
Figure 3 provides a clear example about the limitations of the classical Stanford plot, against the all geometries Stanford-ESA Integrity Diagram. The first row shows the results for the non-safety of life ESTB system and the second row the results for the real EGNOS signal (see also figure 5). The figures at the left show the classical Stanford Plots. The figures at the right show the associated all geometries diagrams. While the Stanford Plot at the top looks like the best performance, with availability of 99.99%, is the Stanford-ESA Integrity Diagram at the bottom who has the best performance.
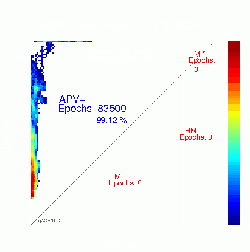
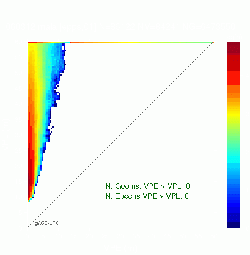
Figure 4 shows another example of how optimistic can the classical Stanford Plot be. The figure at the left show the classical Stanford Plot without having MIs. The figure at the right shows a very unsafe situation with a huge number of geometries having MIs. This result corresponds to an specific critical day of the non-safety of life ESTB system in Canaries Islands (North-West of Africa).
These examples clearly illustrate on the importance of complementing daily user/pseudorange bounding routine performance tests with Stanford-ESA tests around Europe sites, so that all geometries are systematically assessed, confirming hopefully system margins are sound in all circumstances. This may be of particular interest upon major identified GPS or ionospheric threat events, to confirm user domain margins remain constant upon a system maintenance correction, etc.
Figure 3: Two examples comparing the performance of the Stanford Plot and the all geometries Stanford-ESA Integrity Diagram. Each row shows the Stanford Plot and its associated Stanford-ESA Integrity Diagram. The first row corresponds to the non-safety of life EGNOS Test Bed (ESTB) system (PRN 120) and the second row to the real EGNOS signal (PRN 126).
Figure 4: Example of how conservative can the classical Stanford Plot be. No MIs appear in the Stanford Plot, while a very unsafe performance is displayed in the all geometries Stanford-ESA Integrity Diagram. Results computed from the non-safety of life ESTB system signal (PRN 120).
Computation Algorithm
A simple sequential/recursive algorithm to compute the XPE and XPL for all possible geometries of satellites in view with very low storage and CPU requirements is provided at the end of this entry (Appendix).
The algorithm starts up from the normalized geometry matrix and measurement vector for all satellites in view with valid differential corrections available. It excludes one satellite and computes the XPE and XPL; then iterates recursively from previous matrix and vector up to when only 4 satellites remain (i.e., recursively going over one branch in the “combinations tree”). Next, it comes back to the starting matrix, excludes another satellite and recursively iterates again. This scheme is sequentially applied over all the possible branches, covering all combinations of satellites.
The strategy has low storage requirements. Only a single geometry matrix G and measurement vector y have to be stored (at most) at the same time (see note 3 in Appendix). No combination is computed twice.
The previous algorithm has been implemented in BRUS[5], the software developed by the UPC University in Barcelona, Spain, to process and analyze the SBAS data. It has also been incorporated in a testing version of the Global Monitoring System (GMS)[6] that is computing daily the EGNOS performances.
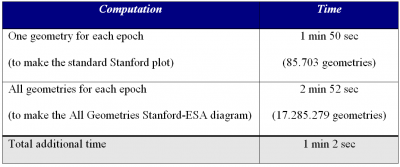
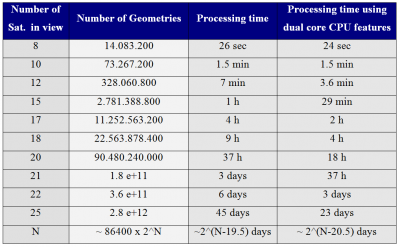
The computation of the “all geometries” Stanford-ESA diagram for the 24h data set at 1Hz of figure 3 (at top), involving 17.285.279 geometries required only 1 min. and 2 sec. of CPU additional to the computation of “one single” geometry for each epoch (see Table 1)
An assessment of the additional computation time required to build the 24h Stanford-ESA Diagram relative to the Stanford plot in function of the number of satellites (continuously) in view is given in table 2. About the 50% of CPU time is devoted to the internal loops, vector assignation … and the other 50% to compute the navigation solution. These results have been computed running the software code of the appendix over a standard PC with Linux (Pentium Dual Core CPU 3.4 GHZ). Two different approaches have been used to compute the processing time:
- one Using the source code given in the appendix in a single processor environment.
- two Optimizing the software code for multicore processors (in the table is shown the behavior in a dual core processor).
The results show that although the number of geometries increases with [math]\displaystyle{ 2^N }[/math], when the number of satellites N is large, the computation of a full 24h data Diagram is feasible having up to 20 satellites in view (with the current computation capabilities of a standard PC). Notice that doubling the number of cores, the CPU time is reduced by half (equivalently, to process one more satellite with the same time).
Previous results suggest that this technique will be feasible for the combined GPS and Galileo constellations, taking into account the computation capabilities evolution (faster clocks and multicore processors).
EGNOS Measurement Results
Stanford-ESA performance results with real EGNOS signal in space were computed for a set of stations covering a wide range of locations in Europe. These results, provided here for illustration, were obtained on March 12th 2006 with PRN 126 EGNOS transmission.
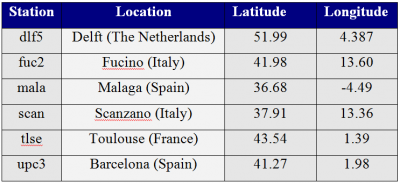
Figure 5, show the all geometries Stanford-ESA Integrity Diagrams in the Vertical domain for 6 fixed sites which coordinates are given in table 3. All data sets were collected at 1Hz.
Results clearly reveal excellent EGNOS integrity margins for all geometries. The integrity margins remain large, and for all samples, it is confirmed that the computed protection levels do always bound the user position error.
A regular daily monitoring of the Stanford-ESA diagrams at several European sites is a very good complement to daily accuracy, availability and continuity performance measurements and could better help to understand the actual EGNOS safety margins, allowing, through real data, to confirm the designed safety margins. This monitoring can be done by a plot such as of Figure 6, derived from the Stanford-ESA Integrity Diagram. Each point in this plot represents the “worse ratio of XPE/XPL” for a given site in 24 hours. Thence, when this value is under 1, it means that at the user domain worse-ever possible case, there is no situation in which the error overcomes the protection level, on this day and for such station
Figure 5: Vertical component: All-Stanford-ESA diagram for 6 sites covering a wide range of locations in Europe at March 12th 2006 (EGNOS, GEO PRN 126). The coordinates are given in Table 3.
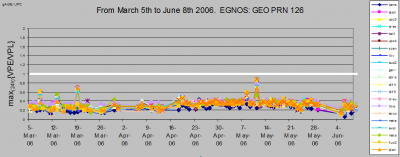
The plot at top of Figure 6 shows how the above mentioned very exigent criterion is fulfilled, in the vertical domain, by all the monitored sites of a wide network of stations in Europe for more than three consecutive months of real EGNOS signal (GEO PRN 126). The same plot, but with the non-safety of life ESTB system signal (GEO PRN 120), is shown at bottom for comparison, illustrating the sensitivity of this plot to the system integrity.
Figure 6: The Worse daily VPE/VPL ratio computed for a network of stations covering a wide range of locations in Europe, from March to June 2006. The plot at top corresponds to the true EGNOS signal (GEO PRN 126). The plot at bottom corresponds to the non-safety of life ESTB system signal (GEO PRN 120).
Conclusions
A new concept for SBAS integrity validation is presented in this work, consisting of a modification of the well-known and extensively used Stanford diagram.
Results show how “unsafe system performances” are amplified by the Stanford-ESA Integrity Diagram (by running for all geometries), proving its ability to better discriminate between safe and unsafe systems, than the classical Stanford Plot. Obviously, with the Stanford-ESA Integrity Diagram the results for accuracy and availability do not have any meaning and the analysis shall only focus on integrity. Indeed, showing that in this user level domain, there is no situation for any possible geometry in which the error overcomes the protection level, then this would be the best experimental guarantee that at user domain, for a specific location and epoch, no over-bounding is incurred. In this way, the computations with real measurement shows that the EGNOS integrity margins remain safe when the Stanford-ESA integrity diagram is computed, a certainly very positive result.
The Stanford-ESA Integrity diagram is a powerful tool for safety analysis, since it may easily be applied to real data, and without significant CPU or storage requirements.
With the mathematical approach presented in the Appendix, the Stanford-ESA diagrams may be computed in real time at any given location. It can be then a complementary real time monitoring for the SBAS operators, allowing the identification in time of possible problems at user level.
Acknowledgement
We would like to thank the European Space Agency, Eurocontrol, The Institut Cartografic de Catalunya (ICC) and the IGS community for providing the ground receiver data. The contributions from gAGE/UPC to this work are done in the frame of EGNOS SIS validation activities carried out as a sub-contract to Pildo Labs, under contract to Eurocontrol.
Appendix: Computation Algorithm
The basic linearized GPS measurement equation [math]\displaystyle{ y = \mathbf{G} x }[/math] with weighting matrix [math]\displaystyle{ \mathbf{W} }[/math] can be transformed into the “normalized” system [math]\displaystyle{ y_W = \mathbf{G_W} x }[/math] with weighting matrix being identity matrix, by introducing the normalized vector [math]\displaystyle{ y_W = \sqrt{\mathbf{W}} }[/math] y </math> and the normalized matrix [math]\displaystyle{ \mathbf{G_W}= \sqrt{\mathbf{W}}\mathbf{G} }[/math]. (Notice that [math]\displaystyle{ \mathbf{W} }[/math] is a diagonal matrix).
- The algorithm:
- 1. Let’s be [math]\displaystyle{ y_W^* = \mathbf{G^*_W} x }[/math] the system after removing the equation of one satellite, and
- [math]\displaystyle{ function_{nav_{sol}} \left(y_w,\mathbf{G_W},k,y^*_W,\mathbf{G^*_W},HPE^*,VPE^*,HPL^*,VPL^*\right) }[/math]
- the function that:
- Removes the row k of matrix [math]\displaystyle{ \mathbf{G_W} }[/math], and the component k of vector [math]\displaystyle{ y_w }[/math], (of orders Nx4 and N, respectively) providing the matrix [math]\displaystyle{ \mathbf{G^*_W} }[/math] and vector [math]\displaystyle{ y^*_w }[/math] (of orders (N-1)x4 and N-1, respectively).
- Computes the XPE* and XPL* from the system [math]\displaystyle{ y^*_W = \mathbf{G^*_W}x }[/math].
- That is:
- INPUT: [math]\displaystyle{ k,y_W,\mathbf{G_W} }[/math]
- INPUT: [math]\displaystyle{ y^*_W,\mathbf{G^*_W},HPE*,VPE*,HPL*,VPL* }[/math]
- That is:
- 2. Let’s be nsat the number of satellites in view with valid differential corrections available:
- For each epoch (having a sample of nsat):
- Compute the XPE and XPL from the system [math]\displaystyle{ y_W=\mathbf{G_W}x }[/math] (solution with all satellites)
- for k1=1, nsat
- [math]\displaystyle{ function_{nav_{sol}} \left(y_w,\mathbf{G_W},k1,y1_W,\mathbf{G1_W},HPE1,VPE1,HPL1,VPL1\right) }[/math]
- for k2=k1, nsat-1
- [math]\displaystyle{ function_{nav_{sol}} \left(y1_w,\mathbf{G1_W},k2,y2_W,\mathbf{G2_W},HPE2,VPE2,HPL2,VPL2\right) }[/math]
- for k3=k2, nsat-2
- [math]\displaystyle{ function_{nav_{sol}} \left(y2_w,\mathbf{G2_W},k3,y3_W,\mathbf{G3_W},HPE3,VPE3,HPL3,VPL3\right) }[/math]
- [math]\displaystyle{ \cdots \cdots }[/math]
- (up to only 4 satellites remain)
- end_for
- end_for
- end_for
- Note: At each iteration, it must be only saved the geometry matrix and measurement vector [math]\displaystyle{ y^*_W,\mathbf{G^*_W} }[/math] as an input for the next one.
- Additional comments:
- Comment 1:
- [math]\displaystyle{ function_{nav_{sol}} \left(y_w,\mathbf{G_W},k,y^*_W,\mathbf{G^*_W},HPE^*,VPE^*,HPL^*,VPL^*\right) }[/math]
- [math]\displaystyle{ x^* = \left( \mathbf{G^{*t}_WG^*_W}\right)^-1 \mathbf{G^{*t}_W} y^*_w }[/math] ; [math]\displaystyle{ P_{x^*} = \left( \mathbf{G^{*t}_W G^*_W}\right)^-1 }[/math]
- where [math]\displaystyle{ \mathbf{G^{*t}_W G^*_W} }[/math] is a 4x4 definite positive matrix.
- If the observation matrix [math]\displaystyle{ \mathbf{G} }[/math] is given in “East, North, and Vertical” coordinates (see appendix E and J [RD.1]),
- thence:
- [math]\displaystyle{ HPE^* = \sqrt{x_1^{*2} + x_2^{*2}} }[/math]
- [math]\displaystyle{ VPE^* = x_3^{*2} }[/math]
- [math]\displaystyle{ HPL^* = k_H \sqrt{ \frac{P_{11}^{*2} + P_{22}^{*2}}{2} + \sqrt{ \left( \frac{P_{11}^{*2} - P_{22}^{*2}}{2}\right)^2} + P_{12}^{*2}} }[/math]
- [math]\displaystyle{ VPL = K_v P_{33}^* }[/math]
- Comment 2:
- A more compact version of the algorithm involving only the storage of single matrix Gw and vector yw could be achieved by using a recursive function:
- function_{nav_{recursive}} (k, kmask, depth, nsat, yw, Gw)
- Being:
- * k, a vector that stores the equivalent k1, k2, k3... of the first version of the algorithm.
- * kmask, a vector which implies a mask for the satellites (so for the rows of Gw and the components of yw), having a value 1 when a satellite is selected for the navigation solution and 0 when it is deselected.
- * depth, the profundity of the present branch inside the tree.
- * nsat, the total number of satellites in view and with valid differential corrections in the present epoch.
- * yw and Gw, the normalized vector and geometry matrix.
- The C “pseudocode” of the function would be:
- function_nav_recursive (k, kmask, depth, nsat, yw, Gw) {
- // To call the function in main:
- // k[0]=0;
- // for (i=0;i<nsat;i++) {
- // kmask[i]=1;
- // }
- // function_nav_recursive (k, kmask, 0, nsat, yw, Gw);
- compute_nav_solution (kmask, nsat, yw, Gw, HPE,VPE,HPL,VPL);
- if ((nsat-depth)>4) {
- for (i=k[depth] ; i<=(nsat-depth-1) ; i++) {
- k[depth+1]=i;
- kmask[i+depth]=0;
- function_nav_recursive (k, kmask, depth+1, nsat, yw, Gw);
- kmask[i+depth]=1;
- for (i=k[depth] ; i<=(nsat-depth-1) ; i++) {
- }
- }
- function_nav_recursive (k, kmask, depth, nsat, yw, Gw) {
- }
- The C “pseudocode” of the function would be:
References
- ^ a b WADGPS Laboratory (Stanford University). "WAAS Precision Approach Metrics. Accuracy, Integrity, Continuity and Availability," October 1997
- ^ SARPS Amendment 77, Annex 10 to the Convention on International Civil Aviation, Aeronautical Telecommunications: International Standards and Recommended Practices, Volume 1, Radio Navigation Aids, November 2002.
- ^ A. Tadjine. “WP 103.2: Integrity at User Level (Part II)”. Issue 1, Rev. B. Ref. GMV-EGNOSAE-TN-007/04. Dated 17/01/2005.
- ^ B.W. Parkinson. Global Positioning System: Theory and Applications, Vol II. Progress in Astronautics and Aeronautics. Vol 164. Published by the Institute of Aeronautics and Astronautics, Inc. 1996.
- ^ Basic Research Utilities for SBAS. M. Hernández-Pajares, J. M Juan and J. Sanz. gAGE/UPC 2003.
- ^ GMS Architectural Design and Detailed Design Document, M. Hernández-Pajares, J. M. Juan and Jaume Sanz. gAGE/EEC, 2004. EUROCONTROL.