If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Solar and Sidereal Times relationship
| Fundamentals | |
|---|---|
| Title | Solar and Sidereal Times relationship |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
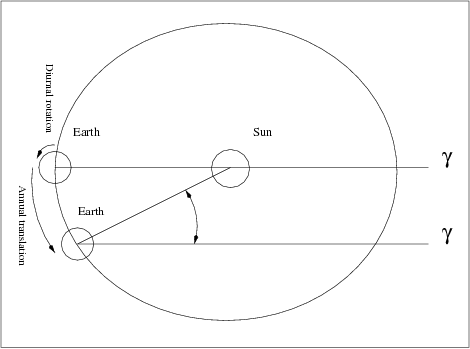
There is a slight difference between a sidereal day and a solar (or synodic day) due to the relative movement between the sun and the earth as a consequence of its annual translation. Figure 1 illustrates the concept.
As it is shown in Figure 1, the Aries reference point ([math]\displaystyle{ \gamma }[/math]), as seen from the earth, apparently moves clockwise during the course of one year (with respect to the sun reference). After one year, the sun and Aries directions coincide again, but the number of laps relative to the sun (solar days) is one less than those relative to Aries (sidereal days).
The difference between the mean sidereal day and mean solar day can be derived approximately as follows: As in a Solar Tropic year [footnotes 1], the mean solar time delayed 1 day respect to the mean sidereal time, thence:
- [math]\displaystyle{ \frac{24^h}{365.2422}\simeq 3^m56^s \qquad \mbox{(1)} }[/math]
Thence, a sidereal day is shorter than the solar day for about [math]\displaystyle{ 3^m56 }[/math].
The conversion between UT1 and Apparent and Mean Sidereal Time is given by equations (2) and (3) (see CEP to ITRF article)
- [math]\displaystyle{ \Theta_{_G}=\theta_{_G} +\alpha _E \qquad \mbox{(2)} }[/math]
- [math]\displaystyle{ \theta_{G_0}=6^h41^m 50^s_{\cdot}54841+8640184_{\cdot}^s812866\,T_u+0_{\cdot}^s093104\,T_u^2-6^s_{\cdot}2 \, 10^{-6}\, T_u^3 \qquad \mbox{(3)} }[/math]
Notes
- ^ Tropic year is the elapsed time between two successive culminations of sun by the Mean Equinox. It has a duration of 365.2422 mean solar days.