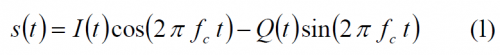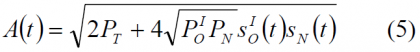If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Linear Modulation (Spatial Combining)
| Fundamentals | |
|---|---|
| Title | Linear Modulation (Spatial Combining) |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
Introduction
The Linear Modulation, also known as additive or spatial modulation, basically consists in the addition of a new ranging signal to either the I or Q phases of a carrier where already at least other two signals are present. A well documented case in navigation is that of the GPS IIR Modernization or GPS IIR-M [P.A. Dafesh et al., 1999][1] and [P.A. Dafesh et al., 2000][2]. In fact, GPS investigated at some point during its modernization the possibility of adding the M-Code in phase with the C/A Code or the P(Y) Code using this technique as shown by [J. W. Betz, 1999] [3] and [S. H. Raghavan et al., 1997][4].
Let as suppose that we want to linearly add a new binary signal [math]\displaystyle{ S_N\left(t\right) }[/math] to a baseband waveform modulated with other two binary signals [math]\displaystyle{ S_O^I\left(t\right) }[/math] and [math]\displaystyle{ S_O^O\left(t\right) }[/math], where the subindex N refers to the new signal, O indicates the old signals that were already on the carrier in quadrature (QPSK) and I and Q are the respective phase. The In-phase and Quadrature components of the new multiplexed signal may be represented by
where the In-phase and quadrature components of the carrier, that is and , are defined as follows:
and,
As we can recognize, the new signal has been added in-phase without loss of generality. If we define now the total power of the signal as
it can be shown that the envelope of the composite signal will adopt the following form:
which is not constant due to the presence of a time-varying component in addition to the constant [math]\displaystyle{ 2P_T }[/math]. This is in principle negative because the result is AM-to-AM and AM-to-PM distortions when the signal is filtered through a nonlinear High Power Amplifier (HPA) unless we work in the linear region, far away from saturation. If this were the case, the operating point of the amplifier would be backed off from its saturation point to the linear region of the amplifier, making in principle this multiplexing approach a suitable alternative.
However, such a back-off is not of interest most of the times due to the high power inefficiency that results. Indeed, as early GPS modernization studies have clearly shown, the back-off functioning of an amplifier working in the linear region can result in several dB of power losses. We will show this in the next section with a particular example of the Linear Modulation, namely the Tri-code Hexaphase Modulation.
Last but not the least, it is important to mention that a Linear modulation is equivalent to spatially combining the signals to multiplex, where a separate amplifier chain and antenna aperture are used to modulate the existing signals and the new signals. This so-called separate aperture implementation results in a significant loss of overall power efficiency since a second power amplifier would be required for the new signals to be modulated.
Tri-code Hexaphase Modulation
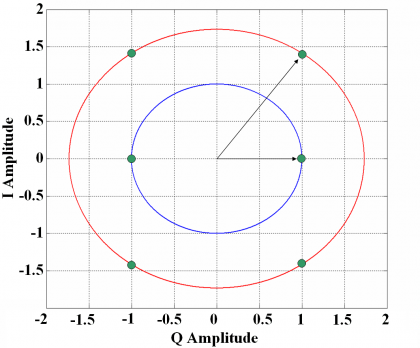
The tri-code Hexaphase modulation is a particular implementation of the Linear Modulation described above. Let us assume as an example that the GPS M-Code and P(Y) Code would have the same power level, being this half of that of the C/A Code. [P.A. Dafesh et al., 2000] [2] have shown that as a result of applying the Linear Modulation, the envelope of the multiplexed signal would not be constant. This is shown in the following figure, where the constellation diagram is depicted.
As we can clearly see, the plot presents two distinct amplitudes since the constellation points lie on two different constant circles. This results in an hexaphase modulation as the name well indicates. In this particular example, the new M-Code was added to the P(Y) Code in-phase (vertical axis in the figure) following the mathematical scheme of (2).
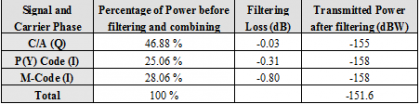
Let us assume now a GPS transmission bandwidth of 30.69 MHz. This results in a filtering loss of approximately 0.03 dB for the C/A Code, 0.31 dB for the P(Y) Code and 0.80 dB for the M-Code. If we further assume same transmission powers as [P.A. Dafesh et al., 2000] [2], the power efficiency of the linear modulation applied to GPS would adopt a value of approximately 93.23 %. This is indeed very close to the figure of the 92.80 % derived by [P.A. Dafesh et al., 2000][2] under similar assumptions.
This means a 0.30 dB power loss in the total signal power due to filtering and the Linear modulation. Although this might seem a good number in principle, the fact is that the overall power efficiency is in reality significantly reduced due to the amplifier back-off operation (unless we employ a separate power amplifier and work with a separate aperture) required to amplify the linearly modulated signals without causing AM-AM or AM-PM distortions. In fact, the 93.23 % power efficiency obtained in the previous analysis does not include the modulator inefficiency that amplifiers present in real world.
In order to avoid the disadvantages of this modulation, constant envelope solutions have been proposed to at least reduce the degradation effects that result from the High Power Amplifier as shown in the patent of [P.A. Dafesh et al., 2006] [5]. We describe them in following chapters.
References
- ^ [P.A. Dafesh et al., 1999] P.A. Dafesh, S. Lazar, and T. Nguyen, Coherent Adaptive Sub-carrier Modulation (CASM) for GPS Modernization, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 1999, January 1999, San Diego, California, USA.
- ^ a b c d [P.A. Dafesh et al., 2000] P.A. Dafesh, L. Cooper, M. Partridge, Compatibility of the Interplex Modulation Method with C/A and P(Y) code Signals, Proceedings of the International Technical Meeting of the Institute of Navigation, ION-GNSS 2000, September 2000, Salt Lake City, Utah, USA.
- ^ [J. W. Betz, 1999] J. W. Betz, The offset carrier modulation for GPS modernization, in Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 1999, pp. 639–648, January 1999, San Diego, California, USA.
- ^ [S. H. Raghavan et al., 1997] S. H. Raghavan, J. K. Holmes, S. Lazar, and M. F. Bottjer, Tricode Hexaphase Modulation for GPS, Proceedings of the 10th International Technical Meeting of the Institute of Navigation, ION-GNSS 1997, 16-19 September, 1997, Kansas City, Missouri, USA.
- ^ [P.A. Dafesh et al., 2006] P.A. Dafesh, Nguyen, M. Tien, Quadrature product sub-carrier modulation system, Patent US 7120198, Granted 10 October 2006.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)