If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Galileo Tropospheric Correction Model
| Fundamentals | |
|---|---|
| Title | Galileo Tropospheric Correction Model |
| Author(s) | A. Martellucci, ESA |
| Level | Intermediate |
| Year of Publication | 2012 |
For GNSS working in L-band the main effects are due to Earth’s atmosphere and the characteristics of the local environment of the receiver. On this sense, Earth’s atmosphere can be classified on troposphere, whose main effect is a group delay on the navigation signal due to water vapour and the gas components of the dry air, this delay is non-dispersive (independent of frequency); and the ionosphere, the ionised part of the atmosphere, that induces a dispersive group delay that is several of orders of magnitude larger than the one from the troposphere. Others ionospheric effects such as scintillations and refraction may be present.
Tropospheric Effects
Due to the refractive index N of the earth’s neutral atmosphere (N > 1) GNSS microwave signals suffer from tropospheric propagation delays. The total tropospheric delay in direction of a particular satellite - slant path delay (SPD) - can be divided into a hydrostatic and a wet component. Using mapping functions, these two delays are projected into zenith direction and viceversa.
- [math]\displaystyle{ SPD \left( \epsilon \right)= m_h \left( \epsilon \right) \cdot ZHD + m_W \left( \epsilon \right) \cdot ZWD \qquad \mbox{(1)} }[/math]
- SPD[math]\displaystyle{ \left( \epsilon \right) = }[/math] slant path delay [m] along elevation angle [math]\displaystyle{ \epsilon }[/math]
- ZHD = zenith hydrostatic delay [m]
- ZWD = zenith wet delay [m]
- [math]\displaystyle{ m_h \left( \epsilon \right), m_W \left( \epsilon \right) }[/math] are the mapping functions of the hydrostatic and wet path delay along elevation angle [math]\displaystyle{ \varepsilon }[/math]
For the mapping functions, [math]\displaystyle{ m_h \left(\epsilon \right), m_W \left(\epsilon \right) }[/math] the model of Niell[1] is currently used.
The ZHD and ZWD are related to the air refractivity N, which in turn is determined by values of air total pressure, P [hPa], temperature, T [K], and water vapour pressure, e [hPa].
- [math]\displaystyle{ N = K_1 \left(P-e \right)+ K_2\frac{e}{T}+ K_3\frac{e}{T^2} \equiv k_1\left(P-e \right)Z_d^{-1} + \left(k_2\frac{e}{T} + k_3\frac{e}{T^2}\right)Z_v^{-1} \qquad \mbox{(2)} }[/math]
[math]\displaystyle{ Z_d }[/math] and [math]\displaystyle{ Z_v }[/math] are the compressibility factors of dry air and water vapour. Capital K is used for the formulation that does not include compressibility. In the following tables some experimental values of air refractivity coefficients available from different authors are given. The uncertainty of air refractivity parameters, with particular regard to [math]\displaystyle{ K_3 }[/math], produces an rms fluctuation of the ZTD of about 6 mm on a global scale.
Author(s) [math]\displaystyle{ K_1 }[/math]
[math]\displaystyle{ [1/hPa] }[/math][math]\displaystyle{ K_2 }[/math]
[math]\displaystyle{ [K/hPa] }[/math][math]\displaystyle{ K_3 * 10^{-5} }[/math]
[math]\displaystyle{ [K^2/hPa] }[/math]Smith & Wintraub[2] 77.607
± 0.01371.6
± 8.53.747
± 0.013Thayer[3] 77.64
± 0.01464.79
± 0.083.776
±0.004Hasegawa & Strokesb[4] 77.6
±0.03269.4
± 0.1463.701
± 0.003Liebe[5] 77.676
± 0.02371.631 3.74656 Bevis
weighted[6]77.6 69.4 3.701 Bevis
unweighted[6]77.6
± 0.0570.4
±2.23.739
± 0.012Rueger
best avail. [7]77.695
± 0.01371.97
± 10.53.75406
± 0.03Rueger
best average. [7]77.689
±0.009471.295
± 1.33.75463
± 0.0076
The zenith hydrostatic delay ZHD can be modelled using total pressure at the antenna site. The model of Saastamoinen [6] is a rather accurate hydrostatic model:
- [math]\displaystyle{ ZHD = \dfrac{0.0022767 \cdot p}{1-0.00266 \cdot cos 2 \varphi - 0.00028 \cdot h} \qquad \mbox{(3)} }[/math]
- [math]\displaystyle{ \varphi }[/math]: Ellipsoidal latitude
- [math]\displaystyle{ h }[/math]: Surface height above the ellipsoid in [km]
- [math]\displaystyle{ p }[/math]: Total Surface pressure in [hPa]
Therefore the ZWD is given by the following integral along the atmospheric profile:
- [math]\displaystyle{ ZWD = 10^{-3} \cdot \int\limits_{h_0}^{\infty}\left( K_2'\frac{e}{T} +K_3\frac{e}{T^2}\right)\,dh \qquad \mbox{(4)} }[/math]
- [math]\displaystyle{ K_2' =K_2 - K_1\frac{M_w}{M_d}= 22.1 [K/hPa] }[/math]
- [math]\displaystyle{ M_d = 28.9644 }[/math] , [math]\displaystyle{ M_w = 18.0152 }[/math] are the Molar weights of dry and wet air [g/mol]
The zenith wet delay can also be estimated, with a reduced accuracy, from the vapour pressure at the height of the receiver, [math]\displaystyle{ e_0 }[/math], and the local climatological parameters,[math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ T_m }[/math] related to the vertical profiles of air total pressure, temperature and water vapour pressure.
- [math]\displaystyle{ ZWD\left(e_0,\lambda,T_M\right) = 10^{-6} \cdot \frac{R_d}{g_m} \cdot \left(K_2' + \frac{K_3}{T_M}\right)\cdot \frac{e_0}{\lambda +1} \approx 10^{-6} \cdot \frac{R_d}{g_m}\frac{K_3}{T_M} \frac{e_0}{\lambda +1} \qquad \mbox{(5)} }[/math]
This equation is assumed to be valid under the following condition [math]\displaystyle{ e = e_0 \left(p/p_0\right)^{\lambda+1} }[/math]
- [math]\displaystyle{ R_d = 287.054 [J/(Kg K)] }[/math]
- [math]\displaystyle{ T_M = \int\limits_{h_0}^{\infty}\frac{e}{T}\,dh / \int\limits_{h_0}^{\infty}\frac{e}{T^2}\, dh = }[/math] Effective Mean temperature of the water vapour column above the receiver [K]
- [math]\displaystyle{ g_m=g\left(\varphi,h_0\right) = 9.784 \cdot \left(1-0.00266 \cdot cos\left(2\cdot\varphi\right)-0.00028\cdot h_0\right) = }[/math] Gravity acceleration at the mass centre of air [math]\displaystyle{ [m/s^2] }[/math]
In the framework of the Galileo project ESA used the European Centre for Medium-Range Weather Forecasts
(ECMWF) reanalysis product ERA15 covering the period from 1979 to 1993 to derive the input parameters and the coefficients for the calculation of ZHD ZWD. ERA15 global fields are characterized by a horizontal resolution of 1.5 x 1.5deg, a vertical resolution of 31 levels and a temporal resolution of 6 hours (00, 06, 12, 18 UTC). The 31 levels are defined in terms of pressure (hPa), with a higher resolution in the planetary boundary layer, where the levels follow the earth surface. Values of temperature (K) and specific humidity (kg/kg), associated with these pressure levels, are also provided with the dataset. The analysis produced among the others, monthly statistics (unconditioned and conditioned to the hour of the day) of “surface data”, [math]\displaystyle{ P\, , e\, , T_m\, , \lambda }[/math], with a world-wide coverage.
Air total pressure, P, is assumed to be affected by a seasonal variation:
- [math]\displaystyle{ X_i\left(D_y\right)=a1_i-a2_i cos \left [ 2\pi \dfrac{\left(D_y-a3_i\right)}{365.25}\right ] \qquad \mbox{(6)} }[/math]
- [math]\displaystyle{ a1_i = }[/math] average value of the parameter
- [math]\displaystyle{ a2_i = }[/math] seasonal fluctuation of the parameter
- [math]\displaystyle{ a3_i = }[/math] day of the minimum value of the parameter
- [math]\displaystyle{ D_y = }[/math] day of the year [1 ..365.25]
In addition [math]\displaystyle{ T_m\, , e\, , \lambda }[/math] are assumed to be affected by both seasonal and diurnal fluctuations:
- [math]\displaystyle{ X_i\left(D_y,H_d\right)=a1_i - a2_i cos \left [ 2\pi \dfrac{\left(D_y-a3_i\right)}{365.25}\right ] - b2_i \left(D_y\right)cos \left [ 2\pi \dfrac{\left(H_d – b3_i \left(D_y\right)\right)}{24}\right ] \qquad \mbox{(7)} }[/math]
- [math]\displaystyle{ H_d = }[/math] hour of the day [0..24)
- [math]\displaystyle{ b2_i = }[/math] amplitude of daily fluctuation.
- [math]\displaystyle{ b3_i = }[/math] hour of the day at which the minimum value occur.
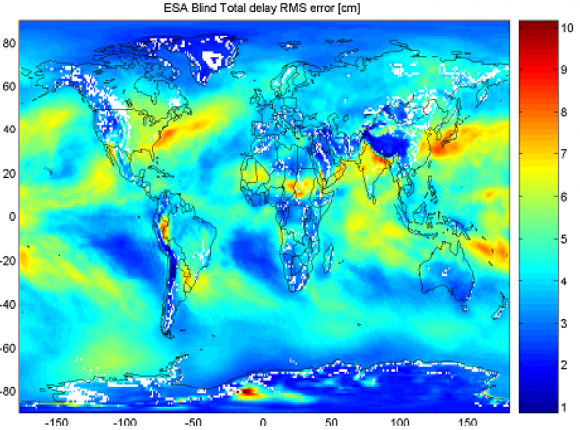
The model has been validated using and independent ECMWF global product covering the period from March to October 2002 with a spatial resolution of 1 x 1 deg. The global map of the model rms error is given in Figure 1. The overall rms errors of ZTD, ZHD and ZWD are 4.5, 1.6 and 4.4 cm with biases of 9, 0.6 and 8 mm, respectively. Those errors can be reduced by using as input actual meteorological ground measurements and as an additional step actual values of [math]\displaystyle{ \lambda }[/math]
The input parameters of the model can be scaled from surface to height h by assuming:
- [math]\displaystyle{ T_m\left(h\right) = T_{ms} - \alpha_m \cdot \left( h - h_s\right) \qquad \mbox{(8)} }[/math]
- [math]\displaystyle{ a_m }[/math] lapse rate of the mean temperature of water vapour, [K/km], also derived from ERA15.
As an example the error of the model at 5000 m, in the upper part of the troposphere, the model error rms reduces to 2.5, 2.2 and 1 cm for ZTD, ZHD and the ZWD.
Notes
The content of this article is based on the paper "Review of tropospheric, ionospheric and multipath data and models for Global Navigation Satellite Systems" presented in the 3rd European Conference on Antennas and Propagation (EuCAP) in 2009, Berlin (Germany). The authors of this paper are A. Martellucci and R. Prieto Cerdeira (European Space Agency)
References
- ^ NIELL, A.E. “Global mapping functions for the atmosphere delay at radio wavelengths”, Journal of Geophysical Research, Volume 101, No B2, pp. 3227-3246, 1996
- ^ E. K. Smith and S. Weintraub, “The Constants in the Equation for Atmospheric Refractive Index at Radio Frequencies”, Proceedings of the institute of Radio Science, 41, pp. 1035-1037, 1953
- ^ G. D. Thayer, “An improved equation for the radio refractive index”, Radio Science, vol. 9, n. 10, pp. 803-807, October 1974
- ^ S. Hasegawa & D. P. Strokesburry, “Automatic digital microwave hygrometer”, Review of Science Instruments, vol. 46, n. 7, July 1975.
- ^ H. J. Liebe, Models of the Refractive Index of the Neutral Atmosphere at Frequencies Below 1000GHz, Chapter II.3.1.2, in The Upper Atmosphere-Data Analysis and Interpretation, edited by Dieminger- Hartmann Leitinger,pp. 270-287, 1996
- ^ a b c M. Bevis and al., “GPS Meteorology: Mapping Zenith Delay onto Precipitable Water”, American Meteorological Society, vol. 33, pp 379-386, 1994
- ^ a b J. M. Rüger, "Refractive Index Formulae for Radio Waves", Proceedings, FIG XXII International Congress, Washington DC, 19-26 April 2002.