WARTK Fundamentals

Fundamentals
Title	WARTK Fundamentals
Author(s)	GMV
Level	Basic
Year of Publication	2011

The Wide Area RTK concept was introduced in the late 1990s to address RTK deficiencies by the Research Group of Astronomy and Geomatics (gAGE) from the Technical University of Catalonia (UPC). The WARTK method increases the RTK/NRTK service area, with permanent stations separated by up to 500–900 kilometers — all while requiring 100 to 1,000 times fewer receivers covering a given region.

WARTK Technique

In RTK technique the differential ionospheric refraction on the signals typically limits the real-time ambiguity resolution (and the corresponding navigation with sub-decimeter errors) to baselines of few tens of km from the nearest reference site. The main techniques supporting this new approach, WARTK, are related to an accurate real-time computation of ionospheric corrections, combined with an optimal processing of GNSS observables (carrier phases in particular) in both 2 and 3-frequency GNSS systems. The navigation can be performed with few centimeters of error at distances of hundreds of kilometers from the nearest reference station.

Figure 1: WARTK Technique (image cortesy of gAGE/UPC)

Indeed, the Ionosphere produces ambiguity estimation biases and correlations whose mitigation is the main problem of several techniques such as LAMBDA method, which takes into account these correlations in order to get reliable ambiguities for short baselines. With this RTK technique several thousands of reference receivers would be needed to provide service to Europe. To solve this limitation, WARTK provides to the users with a very accurate ionospheric refraction estimate to be removed from the user navigation filter equations. This was fulfilled by developing a very precise technique to compute ionospheric corrections in real-time using a 3-D voxel model of the ionosphere, estimated by means of a Kalman filter, and using exclusively GNSS data gathered from fixed receivers separated several hundreds of kilometers. In this way, just few dozens of fixed reference GNSS receivers are enough to ensure a sub-decimeter positioning service at continental scale, over Europe for example.

The ionospheric model running in the WARTK central processing facility (CPF) (see Figure 1), precisely captures the real-time, linear and larger scale electron content variations. The model tomographically maps the ionospheric state as measured by a network o permanent GNSS receivers, each separated up to many hundreds of kilometers. A second component of the model, needed to provide precise ionospheric corrections to the users, characterizes and mitigates ionospheric waves, known as medium scale traveling ionospheric disturbances (MSTID), which are frequent non-linear phenomenon affecting GNSS users at mid latitude. This precise real-time ionopsheric model is well integrated in the geodetic filter of the CPF, and ensures successful ambiguity fixing among the permanent GNSS stations and especially between the rover and the nearest permanent station.

Figure 2: WARTK algorithm layout for the user receiver (image courtesy of gAGE/UPC)

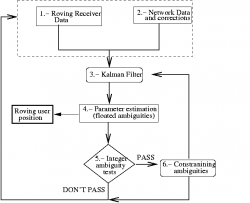
Then, then WARTK user navigation employs multi-frequency carrier phase data, combined with the accurate corrections provided by the CPF, most importantly, ionospheric delay. Once the ionospheric corrections are applied by the user, cycle ambiguities can be fixed either by using a three-carrier ambiguity resolution (TCAR) approach or the well-know LAMBDA method. A layout of this approach for a WARTK user receiver is shown in Figure 2.

WARTK Models and Algorithms

• The Real-time tomographic model.

The free electron density can be described as a random walk process in time that can best be estimated in a Sun-fixed reference frame where it is relatively stationary (variation of 10% during one day in mean latitudes and Solar Maximum conditions). The tomographic model adopted is spatially formed by a set of cells or volume elements (voxels), especially suitable to detect local features, that cover all the ionosphere sampled by the GPS satellite/receiver rays. These voxels, which electron density is considered uniform at any given time, can be taken with the same size for describing a region sampled from an approximately homogeneously distributed network of reference stations. A voxel size of 3x5 degrees in latitude and solar longitude, and two layers with boundaries at 60-740-1420 km have been adopted. This is adequate to get precise ionospheric determinations from ground GPS data.

The resolution of the model initialized with data from the previous day, is performed using the geometry-free combination of phases, [math]\displaystyle{ L_1 }[/math] and [math]\displaystyle{ L_2 }[/math], of the transmitter T measured from the receiver R. The estimation of this ionospheric model is done by means of a Kalman filter with 10 minutes of updating time (similar performance with 2 minutes), in such a way that the results of the last batch are used to estimate the ionospheric delays up to the next updating time. Then, all ionospheric delays are estimated only from the previous data, as must be done in real-time.

• WARTK algorithm user.

There are two different techniques at user level to solve the ambiguity, differentiating between dual-frequency data or 3-frequency data

1. WARTK-2 algorithm: In the case of dual-frequency user, the ambiguity resolution can be obtained with the well-known LAMBDA method, explained in article RTK Fundamentals. The main difference with classical RTK is that the ionospheric delay is much more precise, the one received from the WARTK CPF.
2. WARTK-3 algorithm: For the three frequency case, the ambiguity fixing is done with three-carrier ambiguity resolution (TCAR) approach. Using phases and pseudorange observables in the form of double differences. The extra-widelane and widelane phase combinations are [math]\displaystyle{ s_{ew}=s_1 - s_2 }[/math] and [math]\displaystyle{ s_w=s_1 - s_3 }[/math], being 1, 2 y 3 each frequency. The TCAR method consists of three basic steps:

Step 1) Solve the extra-widelane ambiguity,[math]\displaystyle{ N_{ew} }[/math], with a synthetic wavelength of 7.45 m by subtracting the pseudorange narrowlane and then rounding off the difference to the nearest whole number of wavelengths

[math]\displaystyle{ \quad N_{ew}=Nint [ \lambda_{ew} (s_1 - s_3) -\rho_{narr} ] }[/math]

where [math]\displaystyle{ Nint }[/math] means “rounded off to the nearest integer” and [math]\displaystyle{ \rho_{narr} =c/(f_1+f_3) [(f_1/c)\rho_1 +(f_3/c)\rho_3] }[/math] is the pseudorange narrolane combination that has the same ionospheric delay as the extra-widelane phase. Subtracting [math]\displaystyle{ N_{ew} }[/math] from [math]\displaystyle{ s_{ew} }[/math] gives the unambiguous value of the phase wide lane. Although in some cases excessive pseudorange multipath can diminish the chances for success, this error is typically small compared with the long wavelength of the extra-wide lane.

Step 2) The wide lane combination ambiguity, [math]\displaystyle{ N_{w} }[/math], is estimated by subtracting from the ambiguous wide lane the unambiguous extra-wide lane obtained in step 1, and rounding off the result to the nearest number of whole cycles of the widelane. The difference between them consists mostly of the wide lane ambiguity, and the differential ionospheric refraction (about 0.06 cycles/TECU for a typical set of GNSS frequencies). The nondispersive terms cancel out. The main problems here are the measurement error and multipath in the carrier-phase signals. Since they are much smaller than the widelane wavelength (0.86 m), they are not likely to be an issue.

Step 3) The [math]\displaystyle{ L_1 }[/math] phase ambiguity is derived from the difference between [math]\displaystyle{ s_1 }[/math] and the unambiguous wide lane obtained previously. As before, this difference is rounded off to the nearest integer number of cycles (in this case of [math]\displaystyle{ s_1 }[/math]). Once the two widelanes and L ambiguities have been resolved, the resolution of those for [math]\displaystyle{ L_2 }[/math] and [math]\displaystyle{ L_3 }[/math] is immediate. Typically, the combination of carrier-phase measurement error and multipath is less than 0.2 cycles and can be ignored. The same cannot be said here of the effect of the ionosphere.

It is in step 3 where the WARTK ionospheric correction is introduced: the estimated value of differential iono delay between the rover and the fixed network station is used as the ionospheric correction in step 3.