Baseband Processing

Receivers
Title	Baseband Processing
Author(s)	GMV
Level	Advanced
Year of Publication	2011

The baseband processing block is responsible for processing the down-converted and digitized signal in order to provide GNSS observables: code pseudo-ranges and carrier phase measurements, as well as navigation data. Additional information such as Doppler frequency, Carrier to Noise ratio, lock indicators can also be provided. In most GNSS receivers’ architectures, the baseband processing relies on independent channels that track each satellite signal autonomously. Then the information from each channel is integrated to derive a navigation solution.

Block Diagram

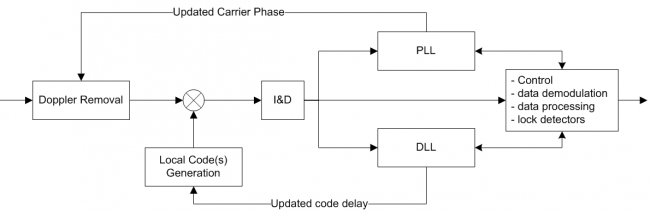
The baseband processing block is usually replicated over several channels. Each channel processes a given signal from a given satellite in order to provide GNSS observables and navigation data. A generic diagram of a single channel within the Baseband Processing block is depicted in the following figure.

Figure 1: Generic Diagram of a single channel in the Baseband Procesing block.

The incoming signal is firstly stripped of its Doppler frequency (according to its current estimation) and then it is correlated with one (or more) PRN codes generated locally (according to the current estimation of code delay). Then new estimations of the Doppler frequency and code delay are computed based on the assessment of the correlation outputs. Please note that for GNSS using FDMA such as GLONASS, the Doppler removal block represents a shift in the frequency not only corresponding to the estimated Doppler shift caused by the relative motion between the satellite and the user, but also to the center frequency of the satellite at hand. This process is implemented in an iterative way, usually using PLL and DLL tracking loops to track the incoming signal phase and code delay respectively. In parallel, the receiver extracts the navigation data of the incoming signal and ensures monitoring and control features further described here.

Principle

The basic principle of GNSS baseband processing relies on the correlation process. The underlying idea is that GNSS signals convey ranging codes that are built such as:

• When the code is correlated with an aligned replica of itself, the correlation output is maximum: high auto-correlation properties
• When the code is correlated with a non-aligned replica of itself, the correlation output is low
• When the code is correlated with another code of the same family, the correlation output is low: low cross-correlation properties

Figure 2: The Correlation process: the receiver shifts the code replica (by changing [math]\displaystyle{ \Delta t }[/math]) until finding a peak in the correlation output.

The basic principle is illustrated in Figure 2: the receiver assigns each channel with a PRN code (for GNSS based on CDMA – such as GPS and Galileo - each satellite transmits a dedicated PRN code, whereas for GNSS based on FDMA – such as GLONASS – the PRN code is the same for all satellites).

At channel level, the incoming signal is correlated with the local replica of this PRN code over time. This local replica is generated such that its code delay and phase vary to represent a two-dimensional search over code and (Doppler) frequency. Whenever the local replica code parameters (code and frequency) match those of the incoming signal, the correlation output will reach a maximum and the receiver will consider this pair (code and frequency) as the current estimates for these parameters.

Real-life systems are very noisy and dynamic: as a consequence, the auto-correlation peak seems to fluctuate at each time instant, hence the need for tracking loops (accumulators and filters) to continuously “follow” the incoming signal, as an error of 1 ms in the code delay would lead to an error of around 300 km in the pseudorange measurement.

Mathematical Model

At the output of the RF section, the baseband signal was written as (neglecting noise):

[math]\displaystyle{ s_{BB} (t_k) = \Re\{s(t_k) exp[j\phi (t_k)]\}\, }[/math]

with [math]\displaystyle{ s(t_k) = A_Im_I(t_k)d(t_k)-jA_Qm_Q(t_k)d(t_k)\, }[/math]

where:

• [math]\displaystyle{ A }[/math] is the signal amplitude
• m(t_k) = ±1 and it includes the PRN code, navigation data (if applicable) and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, [math]\displaystyle{ m_I(t_k) }[/math] and [math]\displaystyle{ m_Q(t_k) }[/math] are the C/A code and the P code respectively
• [math]\displaystyle{ d(t_k) }[/math] is the navigation data. Please note that in case no data is transmitted (e.g. pilot channels) this term is replaced by 1
• I and Q refer to the In-phase and the Quadrature components respectively
• \phi (t_k) accounts for the phase including Doppler frequency, receiver clock instabilities and initial signal phase.

The Doppler removal block rotates the complex baseband signal by the current estimation of the carrier phase:

Related articles

• Generic Receiver Description
• System Design Details
• Antennas
• Receiver Characteristics
• Baseband Processing