If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
NTCM G Ionospheric Model
| Fundamentals | |
|---|---|
| Title | NTCM G Ionospheric Model |
| Level | Intermediate |
| Year of Publication | 2025 |
The NTCM-G (Neustrelitz Total Electron Content Model) ionospheric model is designed to compute ionospheric corrections based on the broadcast coefficients in the navigation message for Galileo single-frequency users. NTCM-G is proposed as an alternative to the NeQuick-G ionospheric model, whose high computational load poses a constraint in those user-segments where the user equipment has limited resources available. This is typically the case of the receivers used in civil aviation and location-based services (e.g., smartphones, UAVs, IoT devices). The NTCM is an empirical model designed to provide a practical and cost-effective solution for estimating global TEC (Total Electron Content). It relies on 12 model coefficients (k₁ to k₁₂), a few fixed empirical parameters, and the solar radio flux index F10.7. To use the NTCM with the broadcast Galileo Effective Ionisation Level coefficients of the navigation message (aᵢ₀, aᵢ₁, aᵢ₂)[1], the F10.7 solar index is replaced by the term Azpar. This term is used as a proxy measure of the solar activity level and is determined as follows: [math]\displaystyle{ Azpar = \left| \sqrt{a_{i0}^2 + 1633.33 \cdot a_{i1}^2 + 4802000 \cdot a_{i2}^2 + 3266.67 \cdot a_{i0} \cdot a_{i2}} \right| }[/math]
Where (aᵢ₀, aᵢ₁, aᵢ₂) are the three Effective Ionisation Level coefficients broadcast in the Galileo navigation message. The Azpar term is used to account for the solar activity dependency (F₅) in the estimation of VTEC (Vertical Total Electron Content) explained below. NTCM-G modeling approach consists of five major dependencies of TEC:
- Local time dependency (F₁)
- Seasonal dependency (F₂)
- Geomagnetic field dependency (F₃)
- Equatorial anomaly dependency (F₄)
- Solar activity dependency (F₅)
The dependencies are combined in a multiplicative way to compute a value of the VTEC:
[math]\displaystyle{ VTEC_{NTCM-G} = F_1 \cdot F_2 \cdot F_3 \cdot F_4 \cdot F_5 }[/math]
Each Fi factor contains the model coefficients (k₁ to k₁₂) for its computation, whose values are provided in Table 3 of the model description document[2].
Input parameters
The input parameters required by the NTCM-G model to estimate each TEC dependency (F₁ to F₅), and consequently the VTEC value, include:
- Galileo Effective Ionisation Level coefficients (aᵢ₀, aᵢ₁, aᵢ₂)
- User receiver and satellite positions in WGS-84 ellipsoidal coordinates (φu, λu, hu) and (φs, λs, hs)
- Universal Time (UT)
- Day of Year (doy)
The output of NTCM-G is the VTEC in TECU for each line of sight between satellite and receiver. The estimated VTEC output can be converted to STEC (Slant Total Electron Content) using the following equation:
[math]\displaystyle{ STEC = MF_{MSLM} \cdot VTEC_{NTCM-G} }[/math]
Where the Modified Single Layer Model (MSLM) mapping function is:
[math]\displaystyle{ MF_{MSLM} = \frac{1}{\sqrt{1 - (\sin z)^2}} }[/math]
[math]\displaystyle{ \sin z = \frac{R_e}{R_e + h_I} \cdot \sin(0.9782 \cdot (\frac{\pi}{2} - E)) }[/math]
With:
- Re = 6371 km (Earth's mean radius)
- hI = 450 km (ionospheric pierce point height)
- E = satellite elevation angle in radians
Ionospheric Delay Calculation
Once the STEC is estimated, the ionospheric propagation delay (in meters) can be computed:
[math]\displaystyle{ I_f = \frac{40.3 \cdot 10^{16}}{f^2} \cdot STEC }[/math]
Where:
- f is the signal frequency in Hz
- The constant 40.3 is in m³/s²/electrons
- 1016 converts TECU to electrons/m²
Higher-order ionospheric terms are generally neglected due to their small magnitude (e.g., < 20 cm for Galileo E1)[3].
Algorithm Steps
To implement the ionospheric correction using NTCM-G for Galileo single-frequency receivers, follow these steps[2] for each satellite-user line-of-sight:
- Obtain receiver (φu, λu, hu) and satellite (φs, λs, hs) positions, and Universal Time (UT), in terms of time of day and month.
- Compute Effectiove Ionization Level Azpar using the broadcast coefficients (aᵢ₀, aᵢ₁, aᵢ₂).
- Calculate satellite elevation (E) and azimuth (A) angles.
- Determine ionospheric pierce point location (φpp, λpp) for the user-to-satellite link at 450km height, and Local Time (LT).
- Use NTCM-G to compute VTEC at (φpp, λpp), LT.
- Calculate mapping function (MF).
- Convert VTEC to STEC using the MF.
- Compute delay using equation for If for the corresponfing frequency to obtain the correction.
- Apply correction to pseudorange.
- Repeat for each satellite.
Under normal ionospheric conditions, variations occur slowly, making high-rate recomputation of delay corrections unnecessary for most applications. A 30-second update interval is generally adequate for stationary receivers or pedestrian users applying the NTCM-G ionospheric model.[2].
Performance
The performance of the NTCM-G model has been validated and compared to the NeQuick-G model. Results indicate that NTCM-G provides generally comparable and sometimes slightly better performance than NeQuick-G[2]. Validation includes comparisons with ground-based VTEC maps from IGS (International GNSS Service), STEC observations, and SPP-based (Single Point Positioning) 3D positioning errors under various geographic and solar activity conditions.
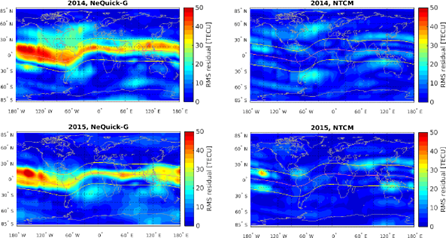 Figure 1: VTEC RMS residual error distribution in 2014 and 2015 for daytime hours 12-15 LT for NeQuick-G (left panel) and NTCM (right panel) [4]
Figure 1: VTEC RMS residual error distribution in 2014 and 2015 for daytime hours 12-15 LT for NeQuick-G (left panel) and NTCM (right panel) [4]
References
- ^ EU, SIGNAL-IN-SPACE INTERFACE CONTROL DOCUMENT, Issue 2.0, enero de 2021
- ^ a b c d DLR, NTCM-G Ionospheric Model Description, mayo de 2022
- ^ M. M. Hoque y N. Jakowski, "Estimate of higher order ionospheric errors in GNSS positioning", Radio Sci., vol. 43, no. 5, 2008, doi:10.1029/2007RS003817.
- ^ M. M. Hoque, N. Jakowski, y J. A. Cahuasqui, «Fast Ionospheric Correction Algorithm for Galileo Single Frequency Users», 2020 Eur. Navig. Conf. ENC, pp. 1-10, nov. 2020, doi: 10.23919/ENC48637.2020.9317502.
