Reference Frames in GNSS

Fundamentals
Title	Reference Frames in GNSS
Author(s)	J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain.
Level	Basic
Year of Publication	2011

Brief descriptions of GPS WGS-84, GLONASS PZ-90 and Galileo GTRF reference frames are provided as follows.

GPS reference frame WGS-84

From 1987, GPS uses the World Geodetic System WGS-84, developed by the US Defence Department, which is a unified terrestrial reference system for position and vector referencing . Indeed, the GPS broadcast ephemeris are linked to the position of the satellite antenna phase centre in the WGS-84 reference frame. Thus, the user receiver coordinates will be expressed in the same ECEF frame.

The initial implementation of WGS-84 was realized from a set of more than a thousand terrestrial sites, which coordinates were derived from Transit observations . Successive refinements (which also leaded to some adjustments of the fundamental constants), using more accurate coordinates of the monitor stations, approximate to some ITRS realizations. For instance, realizations WGS84(G730) and WGS84(G873) correspond to ITRF92 and ITRF94, respectively. The refined frame WGS84(G1150) was introduced in 2002, which agrees with ITRF2000 at the centimetre level.

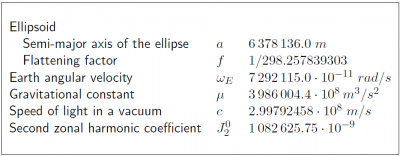
The parameters of the WGS-84 ellipsoid are given in the following Table 1:

Table 1: Ellipsoidal parameters WGS-84 (revised in 1997).

GLONASS reference frame PZ-90

The GLONASS broadcast ephemeris are given in the PZ-90 reference frame. As the WGS-84, this is an ECEF frame with a set of fundamental parameters associated (see table 2 from [GLONASS ICD, 2008]).

The determination of a set of parameters to transform the PZ-90 coordinates to the ITRF97 was the target of the International GLONASS Experiment (IGEX-98). [Boucher and Altamimi, 2001] presents a review of the IGEX-98 experiment and, as a conclusion, they suggest the following transformation from [math]\displaystyle{ (x,y,z) }[/math] in PZ-90 to [math]\displaystyle{ (x',y',z') }[/math] in WGS-84, with a meter level of accuracy.

[math]\displaystyle{ \left [ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ] + \left [ \begin{array}{ccc} -3\,ppb & -353\,mas & -4\,mas\\ 353\,mas & -3\,ppb & 19\,mas\\ 4\,mas & -19\,mas & -3\,ppb\\ \end{array} \right ] \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ] + \left [ \begin{array}{c} 0.07\,m\\ -0.0\,m\\ -0.77\,m\\ \end{array} \right ] \qquad\mbox{(1)} }[/math]

Following the notation of equation of Transformation between Terrestrial Frames:

[math]\displaystyle{ \left ( \begin{array}{c} x\\ y\\ z\\ \end{array} \right )_{_{TRF2}} = \left ( \begin{array}{c} x\\ y\\ z\\ \end{array} \right )_{_{TRF1}} + \left ( \begin{array}{c} T_1\\ T_2\\ T_3\\ \end{array} \right ) + \left ( \begin{array}{ccc} D & -R_3 & R_2\\ R_3 & D & -R_1\\ -R_2 & R_1 & D\\ \end{array} \right ) \left ( \begin{array}{c} x\\ y\\ z\\ \end{array} \right )_{_{TRF1}} }[/math]

the previous transformation (1) is defined by the parameters table:

According to the GLONASS modernisation plan, the ephemeris information implementing the PZ-90.02 reference system was updated on all operational GLONASS satellites from 12:00 to 17:00 UTC, September 20th., 2007. From this time on, the satellites are broadcasting in the PZ-90.02. This ECEF reference frame is an updated version of PZ-90, closest to the ITRF2000.

The transformation from PZ-90.02 to ITRF2000 contains only an origin shift vector, but no rotations nor scale factor, as it is shown in equation (2) [Revnivykh, 2007]

[math]\displaystyle{ \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ]_{ITRF2000} = \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ]_{PZ-90.02} + \left [ \begin{array}{r} -0.36\,m\\ 0.08 \,m\\ 0.18 \,m\\ \end{array} \right ] \qquad\mbox{(2)} }[/math]

The parameters associated to the PZ-90 and PZ-90.02 are given in the next table 2 ([GLONASS ICD, 1998] and [GLONASS ICD, 2008]):

Table 2: Ellipsoidal parameters of PZ-90 and PZ-90.02.

Galileo reference frame (GTRF)

A consortium named the \ac{GGSP}, consisting of seven institutions under the lead of GeoForschungsZentrum Potsdam, is in charge of building up a prototype for the development of the \acf{GTRF} and the establishment of a service with products and information for the potential users. This is a project fully funded by the Sixth Framework Program, under contract by the GSA, to be developed between 2005 and 2009 (http://www.ggsp.eu).

The initial coordinates for the reference stations are provided using GPS observations, because the GTRF is already being required by the time when the first Galileo signals are emitted during the IOV phase. Subsequent GTRF versions will use both GPS and Galileo observations. Weekly solutions will be performed for the long-term maintenance of the GTRF.

The connection to the ITRF is realized and validated by IGS stations , which are part of the ITRF, and especially by local ties to other geodetic techniques like satellite laser ranging and VLBI.

As is the case for GPS and GLONASS, the Galileo satellites will broadcast the satellite orbits in its own GTRF system, which will have centimetre-level alignment to ITRF .