RAIM Algorithms

Fundamentals
Title	RAIM Algorithms
Author(s)	GMV
Level	Basic
Year of Publication	2011

Although conventional RAIM approaches highly improve the receiver’s capacity to detect large errors, their protection levels are not able to cover all user requirements. As an example, the civil aviation community imposes more stringent alert limits whereas Liability Critical Applications rather focus on higher availabilities. Dedicated RAIM algorithms need to be considered according to the application at hand.

RAIM Families

Two main families can be considered:

• Measurement Rejection Approach (MRA)

MRA use Fault Detection and Exclusion (FDE) techniques to ensure that only valid measurements are used in the navigation solution and the respective protection levels computation. These techniques are suited for the civil aviation community but lead to very low solution availability in urban environments, since a large number of measurements is rejected (e.g. due to NLOS multipath).

• Error Characterization Approach (ECA)

It consists on computing protection levels based on the characterisation of the measurement errors; these techniques do not necessarily require FDE techniques. This approach considers the errors in Non Line Of Sight (NLOS) measurements and therefore usually leads to higher protection levels, not fulfilling the stringent civil aviation requirements. Nevertheless, solution availability is considerably higher, making these approaches strong candidates for Liability Critical Applications (LCA) especially in urban environments.

Conventional RAIM

Key Features of traditional RAIM Algorithms:

1. Basic hypothesis: only one satellite is “faulty”, probability of multiple satellite failures at the same time is considered negligible
2. Number of satellites in view determines the possibility of providing integrity
3. Protection levels size depend on satellite geometry (DOP)
4. RAIM algorithms use code measurements
5. Receivers implementing RAIM algorithms are used nowadays for aircraft Lateral Navigation (LNAV) en-route

A few comments on the navigation integrity performance of typical RAIM algorithms:

• Integrity Risk (IR): can be adjusted to the target application by configuration
• Protection Levels (PL): if the integrity risk is configured to 10-7 (e.g. for civil aviation), the values of Horizontal and Vertical PL - HPL and VPL respectively - are higher than the ones provided by a SBAS.
• Time To Alert (TTA): the concept of TTA is meaningless for RAIM algorithms. If the fault detection mechanism (step 1 mentioned above) detects any failure, that measurement is not considered in the solution computation, i.e. the TTA is null since the detection is immediate.

Relative RAIM (RRAIM)

RRAIM uses precise carrier phase measurements to propagate older pseudorange based position solutions forward in time. RAIM is performed on the carrier trajectory to ensure its integrity and then new protection levels are calculated based upon the original values and the accumulated uncertainty over time.

Figure 1:Relative RAIM Concept.

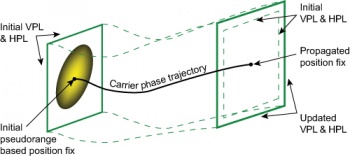
The accumulated uncertainty can be defined as the sum of three sources:

• the change of carrier phase receiver noise and multipath over the propagation time
• the change in tropospheric error over the time interval
• the satellite clock drift over the time interval

Each source can be defined by a Gaussian distribution with a sigma characteristic value, which can be provided a-priori by the GNSS system. RRAIM concept shares the integrity burden between the aircraft, the GNSS constellation and the external monitors which provide the a-priori set of validated measurements. RRAIM propagates both the position and the protection levels, as depicted in the figure.

Algorithms that use past measurements are also called “sequential algorithms” in the literature, as opposed to “snapshot algorithms” that use measurements from a single epoch.

Absolute RAIM

Absolute RAIM is an extension of the conventional RAIM algorithms, using dual frequency measurements that would remove the Ionospheric errors, leading to smaller position errors.

Absolute RAIM would still need some information from the ground segment, such as User Range Accuracies (URA) for each satellite but at low latencies (e.g. 1 hour). In addition, absolute RAIM will greatly benefit from multiple GNSS since its main limitation relies on the geometry and satellite availability. Another advantage of Abolute RAIM is the possibility to relax the integrity requirement for the ground segment by assigning the remaining component to the on-board algorithm.

As a consequence, the following considerations can be made for the Absolute RAIM algorithm for single frequency users:

• The external source should provide information about the ionospheric error. Besides, for aeronautical users this information should be updated frequently. This necessity of ionospheric information for the user will decrease the maximum allowed TTA.
• The magnitude of Protection Levels (PL) will likely be larger for single frequency users than for dual frequency users. These larger PLs may decrease the availability of the services.

Solution Separation RAIM

The maximum solution separation method is based on the observed separation between the position estimate generated by a full-set filter (using all the satellite measurements) and that generated by each one of the subset filters (each using all but one of the satellite measurements).

These techniques can be further extended to include multiple hypotheses. Multiple Hypothesis Solution Separation (MHSS) is a RAIM technique that comprises a protection level computation procedure that admits K simultaneous faulty measurements. MHSS may or may not be accompanied by a fault detection/exclusion (FDE) mechanism. If a FDE mechanism is present, it should be triggered right before the navigation solution and its associated MHSS protection level are computed, and the said computation should use only those measurements that have passed the FDE test successfully.

If the assumption that no more than K measurements can be faulty at the same time is correct, then all faulty measurements (if any) must have been excluded from some of the solutions previously computed, and hence the associated fault-free protection level contains the actual position with its prescribed probability. Thus the region covered by all computed solutions and their protection levels contains the actual position with the prescribed (actually higher) probability. In order to provide a unique navigation solution and an associated protection level, the all-in-view solution (the one using all N measurements) is provided, and the protection level is defined as the minimum circle around it (defined by its radius) such that all other positions together with their associated protection levels are contained within.

Isotropy Based Protection Level (IBPL)

The IBPL algorithm is presented as an example of ECA RAIM family developed for Liability Critical Applications (LCA). The IBPL autonomous technique computes Protection Levels (PL) based on error isotropy, adapting in real-time to ranging error size and considering multiple fault conditions. The main challenge in designing an algorithm for LCA relies in the fact that these applications mostly operate in urban environments, which often have low satellite visibility and large measurement errors caused by Non Line Of Sight (NLOS) signal multipath components. IBPL computes PL based on the all-in-view least squares solution, using the vector of LS estimation residuals as a characterization of the position error: the larger the residual vector, the larger the state estimation error vector (from a statistical perspective). The protection level is computed as:

[math]\displaystyle{ xPL=k.|r|.xDOP }[/math]

Where

• x stands for H or V, horizontal and vertical respectively
• k is the Isotropic Confidence Ratio (ICR), a constant that relates the residual size with the state estimation error, and depends on the target confidence level and the number of measurements used for the estimation
• r is the least squares residual vector

When compared to RAIM algorithms (usually design for civil aviation applications), the IBPL yields high availability at the cost of larger PL in urban environments but also showed great availability in open sky conditions. The advantage of IBPL techniques is that they are completely autonomous.

Related articles

• Integrity
• RAIM
• RAIM Fundamentals
• ARAIM