If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Front End: Difference between revisions
Rui.Sarnadas (talk | contribs) No edit summary |
|||
| Line 122: | Line 122: | ||
where | where | ||
*<math>s(t)=s_I(t)+js_Q(t)</math> is the complex signal to be transmitted | *<math>s(t)=s_I(t)+js_Q(t)\,</math> is the complex signal to be transmitted. | ||
*<math>f_0</math> is the carrier frequency (e.g. L1) for CDMA and it is a sum of all frequencies for FDMA GLONASS signals | *<math>f_0\,</math> is the carrier frequency (e.g. L1) for CDMA and it is a sum of all frequencies for FDMA GLONASS signals. | ||
*<math>\phi</math> is the nominal but ambiguous carrier phase including Doppler frequency | *<math>\phi\,</math> is the nominal but ambiguous carrier phase including Doppler frequency. | ||
| Line 134: | Line 134: | ||
where: | where: | ||
*<math>A</math> is the signal amplitude | *<math>A\,</math> is the signal amplitude. | ||
*m(t) = ±1 and it includes the PRN code, navigation data (if applicable) and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, <math>m_I(t)</math> and <math>m_Q(t)</math> are the C/A code and the P code respectively | *<math>m(t)\,</math> = ±1 and it includes the PRN code, navigation data (if applicable) and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, <math>m_I(t)\,</math> and <math>m_Q(t)\,</math> are the C/A code and the P code, respectively. | ||
*<math>d(t)</math> is the navigation data. | *<math>d(t)\,</math> is the navigation data. Note that in case no data is transmitted (e.g. pilot channels), this term is replaced by 1. | ||
| Line 145: | Line 145: | ||
where <math>\phi (t)</math> now includes receiver clock instabilities | where <math>\phi (t)\,</math> now includes receiver clock instabilities. | ||
| Line 154: | Line 154: | ||
The signal is a complex quantity than can be written in its in-phase (I) and quadrature (Q) components as: | The signal is a complex quantity than can be written in its in-phase (''I'') and quadrature (''Q'') components as: | ||
<math>s_{BB}(t_k)=\Re\{(s_I(t_k)+js_Q(t_k)) exp[j\phi (t_k)]\}\,</math> | <math>s_{BB}(t_k)=\Re\{(s_I(t_k)+js_Q(t_k)) exp[j\phi (t_k)]\}\,</math> | ||
Revision as of 10:51, 6 May 2011
| Receivers | |
|---|---|
| Title | Front End |
| Author(s) | GMV |
| Level | Advanced |
| Year of Publication | 2011 |
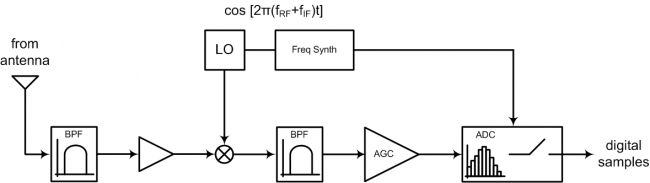
A GNSS signal is captured through the receiver's antenna, and is fed to the front end section. The front end is then responsible for "preparing" the received signals for signal processing tasks, and many different implementations can achieve the desired results. As always, some requirement and trade-off analysis is needed when designing a front-end for GNSS receivers, depending on the application at hand. Figure 1 illustrates a typical front end structure in GNSS receivers.
The frequency synthesizer (shown in Figure 1) provides the receiver with time and frequency reference for all the front end components. Such components, at front end architecture level, gather typical interconnected steps to process and convert a RF signal to a baseband digital signal:
- Filtering and amplification: these stages are necessary to ensure low noise and out-of-band rejection in the received signals, as well as amplification stages to compensate for transmission losses.
- Down-conversion: The front end is responsible for down-converting the signal, whether using direct conversion[1] techniques, to convert the RF spectrum directly to baseband, or heterodyning[2] approaches, where typically a multi-stage approach is used to shift the spectrum to intermediate frequencies (IF), with the appropriate band filtering, ultimately converting the IF signals to baseband[3].
- Quantization: The incoming signals are digitized through analog to digital converters[4] (ADC), ensuring that quantization errors and dynamic ranges are appropriate to accommodate the signal's characteristics.
- Automatic Gain Control: The automatic gain control[5] (AGC) stage is closely related to the down-conversion and quantization steps, and is responsible for adjusting the gain of the front end section in order to take benefit from the full dynamic range.
These operations and different stages in front end signal processing are described in the following sections.
Filtering and Amplification
Due to the GNSS signal's low power upon reception, there is usually a set of filtering and low-noise amplification stages after the antenna. Although the implementation itself varies between architectures and hardware realizations, the principle is the same: the signal is amplified, keeping the noise figure low and rejecting possible out-of-band interference. This can be achieved by alternating Low-Noise Amplifiers (LNA) and filter stages. For more details on amplification, filtering and losses see the antenna section.
Down-conversion
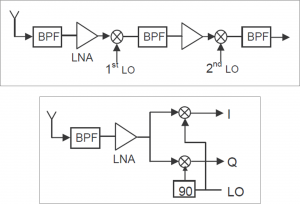
The down-conversion stage's main objective is to convert the input signal from RF to IF and / or to baseband (possibly after a pre-amplification stage). This is achieved through signal mixing operations, such as homodyning and heterodyning, which consist in mixing two different frequency signals in order to shift the same information at two different frequencies, where one is the sum of the two frequencies mixed, and the other is their difference. The basis of the mixing process is the local oscillator (LO), which must be carefully chosen to avoid harmonics and image frequencies near IF. Examples of homodyne and heterodyne mixers are shown in Figure 2.
Heterodyne implementations are the most common. There is typically a two-stage approach, where these multiple stages down-convert the signals to different IF, leading to large separation of image frequencies[6]. Furthermore, this multi-stage design allows for lower quality factor filters, where different trade-offs and fine tuning of derived architectures is more flexible (e.g. the superheterodyne approach). The success of heterodyning is mainly due to the fact that the resulting IF spectrum (lower frequencies than RF) allows for lower cost ADC stages, while using lower quality factor filters. Also, the multi-stage approach enables further filtering of out of band noise and interference, as well as rejection of unwanted frequency images.
For the case of homodyne mixers, there is only a single stage of signal down-conversion, and the local oscillator is tuned at RF. This approach is often referred to as direct conversion, since the mixing at RF converts the RF spectrum directly to baseband. Although an attractive solution, since it eliminates the need for intermediate filters like image frequency removal, direct conversion is challenging due to the need of filters with high quality factors (i.e. increased cost and performance). Another problem is that down-converting directly to baseband shifts harmonics close to zero, making them difficult to filter out.
One topic that is often introduced while discussing down-conversion is direct sampling. Direct RF sampling means exactly that: signals are sampled directly at RF, without down-conversion stages. Although this approach discards mixers and LO in the design, it also requires amplifiers and ADC to operate at RF. As technology goes, hardware components at RF level (around 1.2 GHz to 1.6 GHz) are impractical for mass market applications, for design and component costs. Despite the difficulty to design and implement direct sampling strategies, they have an important advantage of avoiding unwanted signals and errors related to LO mismatches, very common in heterodyne approaches. Also, direct sampling yields reduced sensitivity to clock jitter and noise folding, and the same front-end can be used for all GNSS signals.
Quantization and Sampling
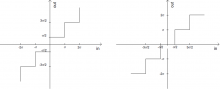
In Analog to Digital Conversion (ADC) there is an inherent quantization process, responsible for the output of a discrete digital signal. Different quantization methods, such as uniform, non-uniform, centered, or non-centered (if there is no zero level) can be used, depending on the noise characteristics, as illustrated in Figure 3.
Although most GNSS receivers use uniform quantization, some non-uniform quantization methods have been proposed showing advantages in the mitigation of Continuous Wave (CW) interference, like Amoroso[7] and DataFusion[8]. Adaptive quantization methods consist in adjusting the quantization levels based on the histogram of the output levels.

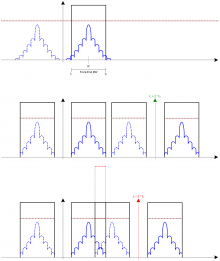
The choice of the quantization method and range depends on the noise characteristics. In GNSS receivers, the power levels of the input signals are low, so the ADC quantization sees only noise-like signals at the input. Figure 4 shows the Signal-to-Noise Ratio (SNR) degradation measured at a receiver’s correlator output. In the figure, precorrelation bandwidth is neglected and infinite sampling rate is assumed, i.e. only the quantization process itself is taken into account.
A uniform quantization with [math]\displaystyle{ k\, }[/math] bits has [math]\displaystyle{ 2k-1\, }[/math] edges, and these quantization edges (thresholds) must be optimized in terms of the noise standard deviation [math]\displaystyle{ \sigma\, }[/math], given by:
[math]\displaystyle{ k = \frac{L}{\sigma}\, }[/math]
Regarding the number of bits to use, it can be seen from Figure 4 that the signal degradation when using 2-bit quantization is about 1.5 dB, increasing to 3.5 dB when using 1-bit quantization[9]. For GNSS signals and receivers, however, these are quite affordable losses for decreasing the number of quantization bits. Although using 1-bit data also discards the need for an AGC (therefore simplifying the hardware), enabling gain control through an AGC system may still help in interference mitigation.
When the ADC samples the input signal (typically at a lower IF frequency after down-conversion), the sampling frequency [math]\displaystyle{ f_s\, }[/math] should be carefully chosen. In fact, for GNSS signals,[math]\displaystyle{ f_s\, }[/math] should not be a multiple of 1.023 MHz. As stated by the Nyquist–Shannon sampling theorem[10], the sampling frequency [math]\displaystyle{ f_s\, }[/math], needed to represent and reproduce the signal, is related to the one-sided baseband bandwidth [math]\displaystyle{ B\, }[/math] by:
[math]\displaystyle{ f_s \gt 2 B\, }[/math]
The signal centre frequency and spectrum is shifted and added [math]\displaystyle{ N\, }[/math] times over the full spectrum. The resulting replicas at [math]\displaystyle{ \pm N \times f_s\, }[/math] must not overlap to avoid aliasing[11] effects. These sampling effects are illustrated in Figure 5.
Automatic Gain Control
The AGC section is an adaptive system, implemented as a feedback loop, to increase the dynamic range to control the quantization levels, and optimize the ratio [math]\displaystyle{ k\, }[/math] between the quantization threshold and RMS noise (as described in the quantization section):
[math]\displaystyle{ k = \frac{L}{\sigma}\, }[/math]
For automatic gain control, different implementations can be used. The most common implementation is to adjust the signal gain depending on incoming signal levels (i.e. an estimate of the noise standard deviation, [math]\displaystyle{ \sigma\, }[/math]). This AGC mode operates completely in the analog domain. An alternative approach is to use the ADC output levels to adjust the AGC gain by preserving the Gaussian shape of ADC output samples, and mapping the ADC output power to ADC input power.
However, classical implementations of automatic gain control do not work well in the presence of continuous wave (CW) interference, and the SNR degradation is about 10 dB for a Jammer-to-Noise ratio (J/N) of 20 dB. To mitigate this effect, the quantization interval can be dynamically adjusted, or overquantization can be used to increase the AGC dynamic range. In the presence of pulsed interference, using additional quantization bits allows for techniques such as digital blanking to be implemented: the quantized value is compared to a threshold (which is often dynamic), and the samples that exceed the threshold are set to zero.
Signal Bandwidth
Besides electrical considerations, the GNSS receiver RF section (antenna and front end) must also take into account the signal structure in terms of spectrum and bandwidth, and should be selected in accordance with the envisaged usage and application.
New constellations and modulations bring different spectrum allocations and bandwidths. As an example, Table 2 illustrates GPS L1 and Galileo E1 bands (which share the same centre frequency), and some characteristic parameters of the incoming signals[12].
| GPS L1 C/A (BPSK) | Galileo E1 B/C (BOC) | Galileo E1 B/C (CBOC) | |
|---|---|---|---|
| Chip Rate [Mcps] | 1.023 | 1.023 | 1.023 / 6.138 |
| Primary Code Length [chips] | 1023 | 4092 | 4092 |
| Primary Code length [ms] | 1 | 4 | 4 |
| Symbol Rate [sps] | 50 | 250 | 250 |
| Centre Frequency [MHz] | 1575.42 | ||
| Receiver Reference Bandwidth [MHz] | 4.092 | 8.184 | 24.552 |
For the GPS case, if a receiver only tracks the C/A code on L1, the antennas (and receiver) need to accommodate bandwidths of approximately 4.092 MHz for a near-optimal bandwidth usage. For Galileo E1 signals, however, due to signal design and spread spectrum properties, the bandwidth doubles. Of course, the more frequency content of the received satellite signals is processed, the better the accuracy performance will be, so a dual-constellation receiver for GPS L1 and Galileo E1 using only one antenna with the maximum bandwidth required would maximize the benefits from using signals from GPS and Galileo.
Dual-frequency receivers used dual-band antennas, and their front end bandwidth is dimensioned to the envisaged application, needed accuracy, and available technology. For example, a survey receiver will need larger bandwidths to achieve accurate results, whereas a low-cost receiver may only have an antenna/front end bandwidth of around 2 MHz, but still receive enough signal power to determine position with an accuracy within meters. Although the receiver’s antenna/front-end bandwidth is directly proportional to the accuracy required for the application, it is also directly proportional to the processing load and power consumption for portable solutions.
From RF to Baseband
In terms of signal representation, the incoming GNSS signal can be written as (neglecting noise):
[math]\displaystyle{ s_{RF} (t) = \Re\{s(t)exp[j(2 \pi f_0t + \phi(t))]\}\, }[/math]
where
- [math]\displaystyle{ s(t)=s_I(t)+js_Q(t)\, }[/math] is the complex signal to be transmitted.
- [math]\displaystyle{ f_0\, }[/math] is the carrier frequency (e.g. L1) for CDMA and it is a sum of all frequencies for FDMA GLONASS signals.
- [math]\displaystyle{ \phi\, }[/math] is the nominal but ambiguous carrier phase including Doppler frequency.
As an example, GPS L1 signal can be written as:
[math]\displaystyle{ s_{RF} (t) = A_Im_I(t)d(t)cos[2\pi f_0t+\phi(t)]-A_Qm_Q(t)d(t)sin[2\pi f_0t+\phi(t)]\, }[/math]
where:
- [math]\displaystyle{ A\, }[/math] is the signal amplitude.
- [math]\displaystyle{ m(t)\, }[/math] = ±1 and it includes the PRN code, navigation data (if applicable) and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, [math]\displaystyle{ m_I(t)\, }[/math] and [math]\displaystyle{ m_Q(t)\, }[/math] are the C/A code and the P code, respectively.
- [math]\displaystyle{ d(t)\, }[/math] is the navigation data. Note that in case no data is transmitted (e.g. pilot channels), this term is replaced by 1.
This received signal is then down-converted to an intermediate frequency:
[math]\displaystyle{ s_{IF} (t) = \Re\{s(t) exp[j(2 \pi f_{IF}t + \phi (t))]\}\, }[/math]
where [math]\displaystyle{ \phi (t)\, }[/math] now includes receiver clock instabilities.
At this stage, the down-converted signal is sampled in the ADC and then mixed with both a local digital sinusoidal wave and a 90-degree shifted version of it. This mixing process converts the IF signal to baseband and preserves phase information:
[math]\displaystyle{ s_{BB} (t_k) = \Re\{s(t_k) exp[j\phi (t_k)]\}\, }[/math]
The signal is a complex quantity than can be written in its in-phase (I) and quadrature (Q) components as:
[math]\displaystyle{ s_{BB}(t_k)=\Re\{(s_I(t_k)+js_Q(t_k)) exp[j\phi (t_k)]\}\, }[/math]
Finally, the resulting baseband signal is fed to the baseband processing block in the receiver.
Related articles
- Generic Receiver Description
- System Design Details
- Antennas
- Receiver Characteristics
- Baseband Processing
References
- ^ http://www.gpsworld.com/gnss-system/galileo/pulling-wideband-7053
- ^ wikipedia:Heterodyne receiver
- ^ wikipedia:Digital down converter
- ^ wikipedia:Analog-to-digital converter
- ^ wikipedia:Automatic gain control
- ^ wikipedia:Image frequency
- ^ Amoroso F., "Adaptive A/D Converter to Suppress CW Interference in DSPN Spread-Spectrum Communications", IEEE Transactions on Communications, Vol. Com 31, No.10, October 1983.
- ^ K. Krumvieda et al. "A Complete IF Software GPS Receiver: A Tutorial about the Details", ION GPS 2001, pp. 789-810.
- ^ a b F. Bastide, D. Akos, C. Macabiau, B. Roturier, “Automatic Gain Control (AGC) as an Interference Assessment Tool”, Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS/GNSS 2003), September 9 - 12, 2003, Portland, OR, Page(s): 2042 – 2053.
- ^ wikipedia:Nyquist–Shannon sampling theorem
- ^ wikipedia:Aliasing
- ^ Kaplan, E.D. et al, "Understanding GPS: Principles and Applications", second edition.