If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Delay Lock Loop (DLL): Difference between revisions
No edit summary |
|||
| Line 9: | Line 9: | ||
Delay Lock Loops are part of the Tracking Loops and aim at tracking the code delay of the incoming GNSS signal, providing a correction the delay | Delay Lock Loops are part of the Tracking Loops and aim at tracking the code delay of the incoming GNSS signal, providing a correction the delay to be used in the local replica code generations. | ||
==Principle == | ==Principle == | ||
The Delay Lock Loop (DLL) tracks and estimates the current misalignment between the [[Multicorrelator|locally generated PRN code replica]] and the incoming signal | The Delay Lock Loop (DLL) tracks and estimates the current misalignment between the [[Multicorrelator|locally generated PRN code replica]] and the incoming signal, within the [[Tracking Loops|tracking loops]]. | ||
For that purpose, the DLL uses integrations, filters and Numerical Control Oscillators (NCO) – described [[Tracking Loops|here]] – as any other loop. | For that purpose, the DLL uses integrations, filters and Numerical Control Oscillators (NCO) – described [[Tracking Loops|here]] – as any other loop. | ||
The DLL | The specificity relies on the discriminator used to assess the error of the current delay estimate. | ||
This principle is illustrated in Figure 1, where the Early and Late correlations are shown, as well as | |||
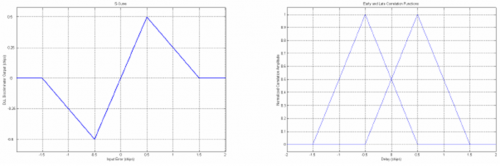
The DLL actually uses [[Multicorrelator|two additional correlators]]: Early and Late, which are delayed and advanced replicas of the prompt code. The difference between the Early and the Late correlators produces a so called S-curve. The DLL actually tracks the zero crossing of this S-curve in order to estimate the current error, which is then feedback to the local code generation block to correct the previous estimate of the incoming code delay. | |||
This principle is illustrated in Figure 1, where the Early and Late correlations are shown, as well as the S-curve produced by their difference. | |||
Revision as of 22:59, 5 May 2011
| Receivers | |
|---|---|
| Title | Delay Lock Loop (DLL) |
| Author(s) | GMV |
| Level | Advanced |
| Year of Publication | 2011 |
Delay Lock Loops are part of the Tracking Loops and aim at tracking the code delay of the incoming GNSS signal, providing a correction the delay to be used in the local replica code generations.
Principle
The Delay Lock Loop (DLL) tracks and estimates the current misalignment between the locally generated PRN code replica and the incoming signal, within the tracking loops. For that purpose, the DLL uses integrations, filters and Numerical Control Oscillators (NCO) – described here – as any other loop.
The specificity relies on the discriminator used to assess the error of the current delay estimate.
The DLL actually uses two additional correlators: Early and Late, which are delayed and advanced replicas of the prompt code. The difference between the Early and the Late correlators produces a so called S-curve. The DLL actually tracks the zero crossing of this S-curve in order to estimate the current error, which is then feedback to the local code generation block to correct the previous estimate of the incoming code delay. This principle is illustrated in Figure 1, where the Early and Late correlations are shown, as well as the S-curve produced by their difference.
As shown previously, the expressions for the Early and Late replicas are given by:
[math]\displaystyle{ I_E = Ad R_{x} (\tau_e-\frac{\delta}{2}) cos(\phi_e) }[/math]
[math]\displaystyle{ Q_E = -AdR_{x}(\tau_e-\frac{\delta}{2})sin(\phi_e) }[/math]
[math]\displaystyle{ I_L = Ad R_{x} (\tau_e+\frac{\delta}{2}) cos(\phi_e) }[/math]
[math]\displaystyle{ Q_L = -AdR_{x}(\tau_e+\frac{\delta}{2})sin(\phi_e) }[/math]
where
- [math]\displaystyle{ \tau_e }[/math] is the error of the code delay estimated at the receiver
- [math]\displaystyle{ \phi_e }[/math] is the error of the carrier phase estimated at the receiver
- E, P, L indexes stand for Early, Prompt and Late respectively
- [math]\displaystyle{ \delta }[/math] is the Early-Late spacing
- A is the amplitude
- d is the navigation message
Discriminators
Two of the most commonly used discriminators are [1]:
- Noncoherent Early minus Late Power (NELP)
[math]\displaystyle{ \frac{(I_E^2 + Q_E^2) – (I_L^2 + Q_L^2)}{2} }[/math]
- Dot Product
The quasi-coherent dot product power discriminator can be written as:
[math]\displaystyle{ \frac{[(I_E - I_L) I_P] + [(Q_E - Q_L) Q_P]}{2} }[/math]
Whenever the PLL is locked, the coherent dot product can be used, with lower computational burden:
[math]\displaystyle{ \frac{(I_E - I_L) I_P}{2} }[/math]
- Normalized Early minus Late Envelope (NELE)
[math]\displaystyle{ \frac{1}{2} \frac{(E - L)}{E + L} }[/math]
Where
- [math]\displaystyle{ E= \sqrt{I_E^2+Q_E^2} }[/math]
- [math]\displaystyle{ L= \sqrt{I_L^2+Q_L^2} }[/math]
Normalized versions of the discriminators are often used in order to remove amplitude sensitivity (especially useful in environments where the carrier to noise ratio changes rapidly).
Performance
In optimal conditions, the main sources of errors in the DLL are thermal noise code jitter and dynamic stress error [1]. Using techniques such as carrier aiding, the dynamic stress error of the DLL can be greatly reduced, leaving thermal noise as the main error source.
The thermal noise code tracking jitter (in chips) for a noncoherent DLL discriminator considering BPSK modulations can be approximated by[1]:
[math]\displaystyle{ \sigma_{th}=\frac{1}{T_c} \sqrt {\frac{B_n \int_{-B_{fe}/2}^{B_{fe}/2} S_s(f)sin^2(\pi f \delta T_c)df}{(2 \pi)^2 C/N_0 [\int_{-B_{fe}/2}^{B_{fe}/2} f S_s(f)sin(\pi f \delta T_c)df]^2}} \times \sqrt { 1 +\frac {\int_{-B_{fe}/2}^{B_{fe}/2} S_s(f)cos^2(\pi f \delta T_c)df} { T C/N_0 [\int_{-B_{fe}/2}^{B_{fe}/2} S_s(f)cos(\pi f \delta T_c)df]^2}} }[/math]
Where
- [math]\displaystyle{ T_c }[/math] is the chip period [s]
- [math]\displaystyle{ R_c }[/math] is the chipping rate [chip/s]
- [math]\displaystyle{ B_{fe} }[/math] is the double sided front-end bandwidth [Hz]
- [math]\displaystyle{ B_{n} }[/math] is the loop noise bandwidth [Hz]
- [math]\displaystyle{ S_s(f) }[/math] is the power spectral density of the signal, normalized to unit area over infinite bandwidth
- [math]\displaystyle{ \delta }[/math] is the Early-Late spacing</math>
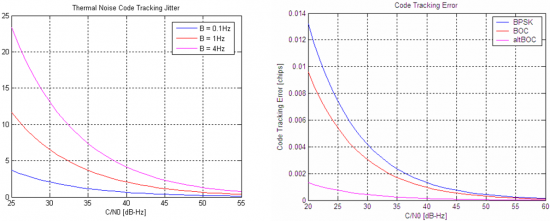
Figure 2 depicts the code tracking error (due to thermal noise) for different loop noise bandwidths but also different modulations, namely BPSK(1), BOC(1,1) and AltBOC (15,10).
These results illustrate the fact that lower loop noise bandwidths (and longer integration times) lead to noise reduction and hence higher performances, as discussed previously. The impact of the modulations is mainly translated by the power spectral density, i.e. the spreader the signal (narrow correlation peaks), the higher performances can be reached.
Related articles
- Generic Receiver Description
- Baseband Processing
- Digital Signal Processing
- Tracking Loops
- Phase Lock Loop (PLL)
- Frequency Lock Loop (FLL)