If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Tracking Loops: Difference between revisions
(→Aiding) |
|||
| Line 13: | Line 13: | ||
==Block Diagram== | ==Block Diagram== | ||
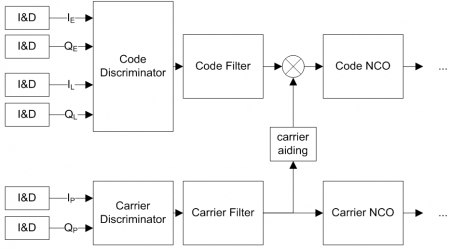
In order to extract information from the incoming signals, GNSS receivers track them by replicating | In order to extract information from the incoming signals, GNSS receivers track them by replicating the PRN code and adjusting its code delay and carrier phase continuously so as to guarantee synchronization with the incoming signal. | ||
In its most common implementation, the receiver implements code and carrier tracking loops to achieve synchronization with the incoming signal, as depicted in Figure 1. | In its most common implementation, the receiver implements code and carrier tracking loops to achieve synchronization with the incoming signal, as depicted in Figure 1. | ||
| Line 22: | Line 22: | ||
The tracking loops include: | The tracking loops include: | ||
*<b>Integrate & Dump (I&D)</b> blocks that accumulate the [[Correlators|correlators’]] outputs and provide their in-phase and quadrature components. | *<b>Integrate & Dump (I&D)</b> blocks that accumulate the [[Correlators|correlators’]] outputs and provide their in-phase and quadrature components. | ||
*<b>Discriminators</b>: process the correlators’ outputs to provide measurable quantities (e.g. carrier phase information) | *<b>Discriminators</b>: that process the correlators’ outputs to provide measurable quantities (e.g. carrier phase information) | ||
*<b>Filters</b>: filter the discriminators’ outputs to reduce noise | *<b>Filters</b>: that filter the discriminators’ outputs to reduce noise | ||
*<b>NCO</b>: Numerical Control Oscillators convert the filter outputs into usable correction factors of Doppler frequency and code delay that are feedback to the Doppler removal and Local code Generators blocks respectively, as shown [[Digital Signal Processing|here]] | *<b>NCO</b>: Numerical Control Oscillators convert the filter outputs into usable correction factors of Doppler frequency and code delay that are feedback to the Doppler removal and Local code Generators blocks respectively, as shown [[Digital Signal Processing|here]] | ||
While code tracking loops follow the code delay of the incoming signal using [[Delay Lock Loop (DLL)| Delay Lock Loops (DLL)]], carrier tracking loops can be designed to follow either the phase of the incoming signal – using [[Phase Lock Loop (PLL)| Phase Lock Loops (PLL)]] or the Doppler frequency of the incoming signal using [[Frequency Lock Loop (FLL)| Frequency Lock Loops (FLL)]]. | |||
Furthermore, receivers may implement both FLLs and PLLs. This decision, together with the dimensioning of | Furthermore, receivers may implement both FLLs and PLLs. This decision, together with the dimensioning of all the components within the tracking loops is part of a series of trade-offs conducted during receiver design. | ||
As an example, the selection of the integration times in I&D blocks (also discussed [[Baseband Processing|here]]), is a trade-off between accuracy and robustness to receiver dynamics. On one hand, the longer the integration time, the less noise is expected at the correlators’ outputs. On the other hand, shorter integration times are more robust in high dynamic stress signal conditions. | As an example, the selection of the integration times used in I&D blocks (also discussed [[Baseband Processing|here]]), is a trade-off between accuracy and robustness to receiver dynamics. On one hand, the longer the integration time, the less noise is expected at the correlators’ outputs. On the other hand, shorter integration times are more robust in high dynamic stress signal conditions. | ||
==Loop Filters== | ==Loop Filters== | ||
Revision as of 17:24, 5 May 2011
| Receivers | |
|---|---|
| Title | Tracking Loops |
| Author(s) | GMV |
| Level | Advanced |
| Year of Publication | 2011 |
GNSS receivers’ goal is to synchronize a local replica of the transmitted PRN Code with the incoming signal in order to estimate the distance travelled by the incoming signal as accurately as possible. For that purpose, tracking loops are used in a closed loop in order to follow continuously the code and carrier parameters of the incoming signal; these loops are often designated as code and carrier tracking loops.
Block Diagram
In order to extract information from the incoming signals, GNSS receivers track them by replicating the PRN code and adjusting its code delay and carrier phase continuously so as to guarantee synchronization with the incoming signal. In its most common implementation, the receiver implements code and carrier tracking loops to achieve synchronization with the incoming signal, as depicted in Figure 1.
The tracking loops include:
- Integrate & Dump (I&D) blocks that accumulate the correlators’ outputs and provide their in-phase and quadrature components.
- Discriminators: that process the correlators’ outputs to provide measurable quantities (e.g. carrier phase information)
- Filters: that filter the discriminators’ outputs to reduce noise
- NCO: Numerical Control Oscillators convert the filter outputs into usable correction factors of Doppler frequency and code delay that are feedback to the Doppler removal and Local code Generators blocks respectively, as shown here
While code tracking loops follow the code delay of the incoming signal using Delay Lock Loops (DLL), carrier tracking loops can be designed to follow either the phase of the incoming signal – using Phase Lock Loops (PLL) or the Doppler frequency of the incoming signal using Frequency Lock Loops (FLL).
Furthermore, receivers may implement both FLLs and PLLs. This decision, together with the dimensioning of all the components within the tracking loops is part of a series of trade-offs conducted during receiver design.
As an example, the selection of the integration times used in I&D blocks (also discussed here), is a trade-off between accuracy and robustness to receiver dynamics. On one hand, the longer the integration time, the less noise is expected at the correlators’ outputs. On the other hand, shorter integration times are more robust in high dynamic stress signal conditions.
Loop Filters
The objective of the loop filters is to filter the discriminator output in order to reduce noise. These measurements are fed to the loop Numerical Control Oscillators (NCO) that subtract them from the original input signal to produce a correction factor which is fed back into the first blocks of the channels, namely Doppler removal and local replica generator, so as to update the current estimations.
The design of the loop filters consists in dimensioning the filter order and bandwidth in order to determine its response to the signal dynamics.
In general, the design of the filter noise bandwidth, [math]\displaystyle{ B_n }[/math] needs to consider the Integration time, T, so that [math]\displaystyle{ B_nT \lt \lt 1 }[/math]. In fact, whenever this condition is not guaranteed, the actual bandwidth tends to be larger than the desired one leading to filter instability.
The effect of the filter noise bandwidth is illustrated in Figure 2, which depicts the filter response to a phase step. It can be seen on one hand, that lower bandwidths present less noisy results (since they correspond to longer integration times). On the other hand, higher bandwidths have faster response times.
As for filter order, the higher the order, the better the capability of the filter to follow the LOS dynamics.
As such:
- 1st order filters are sensitive to velocity stress
- 2nd order filters are sensitive to acceleration stress
- 3rd order filters are sensitive to acceleration stress
As consequence, higher order filters perform better in dynamic stress conditions and provide less noisy results. The drawback relies mainly on the additional computational burden of the filters, since the order of the filter is directly related to the amount of operations. Furthermore, the order of the filter imposes a limit on the filter bandwidth. As an example, a third order filter would require a noise bandwidth below 18 Hz in order to guarantee stability[1].
Aiding
Noting that the carrier loop jitter is much less noisy than the code loop jitter, it is possible to use the measurements from the carrier loop to remove the LOS (Line Of Sight) dynamics of the code loop, with the advantage of being able to lower the order of the code loop filter, as well as its bandwidth. This architecture is often called carrier-aiding and it allows having a 3rd order PLL filter feeding its information to a 2nd order DLL filter, maintaining the same levels of performance of an unaided 3rd order DLL filter.
For that purpose, a scale factor needs to be applied to the carrier filter outputs before including them in the code loop in order to account for the fact that the Doppler effect on the signal is inversely proportional to its wavelength[1]:
[math]\displaystyle{ SF=\frac{R_c}{f_L} }[/math]
Where:
- [math]\displaystyle{ R_c }[/math] is the code chipping rate of the signal at hand
- [math]\displaystyle{ f_L }[/math] is the carrier frequency of the signal at hand
Other ways to remove higher order dynamics from the loops is to use external inertial sensors; also allowing lowering the order of the filters of the tracking loops[2], or further implement piggyback loops.
Related articles
- Generic Receiver Description
- System Design Details
- Antennas
- Receiver Characteristics
- Baseband Processing
References
- ^ a b Kaplan E.D., Hegarty C.J.,"Understanding GPS: Principles and Applications", second edition
- ^ ”Development of INS-Aided GPS Tracking Loop and Flight Test Evaluation”, Toshiaki Tsujii1, Takeshi Fujiwara, Yoshimitsu Suganuma, Hiroshi Tomita,and Ivan Petrovski, Aviation Program Group, Japan Aerospace Exploration Agency, iP-Solutions, Tokyo, Japan