PPP Fundamentals

Fundamentals
Title	PPP Fundamentals
Edited by	GMV
Level	Basic
Year of Publication	2011

Precise Point Positioning (PPP) is a global precise positioning service using all the available GNSS constellations. PPP requires the availability of precise reference satellite orbit and clock products using a network of GNSS reference stations distributed worldwide. Combining the precise satellite positions and clocks with a dual-frequency GNSS receiver, PPP is able to provide position solutions at centimeter level. Accuracy performance can be even better, e.g., sub-centimeter level, in post-processing and in static mode.

PPP Algorithm

The PPP algorithm uses as input both code and phase observations from a dual-frequency receiver., and These are then combined with precise satellite orbits and/ clocks and with additional very accurate error models, in order to calculate precise receiver coordinates and clock. The dual frequency observables are used un-differenced and combined into the so-called ionosphere-free combination, which allows for the removal of the first order effect of the ionosphere.. The highlights of the algorithm are described next. Traditionally, L1 and L2 observables have been used for the PPP ionosphere-free combination in GPS. However, as modernized GPS and Galileo provide carrier-phase observables also in the L5/E5 frequency bands, the following mathematical details have been described for two generic carrier frequencies [math]\displaystyle{ f_A }[/math] and [math]\displaystyle{ f_B }[/math]. At a given epoch, and for a given satellite, the simplified observation equations are presented next:

C_hex [math]\displaystyle{ l\lt sub\gt {P}\lt /sub\gt =\rho+c(b_{Rx}-b_{Sat} )+Tr+\varepsilon_P \qquad \mbox{(1)} }[/math]

[math]\displaystyle{ l_\phi =\rho+c(b_{Rx}-b_{Sat} )+Tr+〖N\lambda+\varepsilon〗_\phi \qquad \mbox{(2)} }[/math]

Where:

[math]\displaystyle{ l_P }[/math] is the ionosphere-free combination of L1 and L2 pseudoranges;

[math]\displaystyle{ l_\phi }[/math] is the ionosphere-free combination of L1 and L2 carrier phases;

[math]\displaystyle{ b_{Rx} }[/math] is the receiver clock offset from the reference (GPS) time;

[math]\displaystyle{ b_{Sat} }[/math] is the satellite clock offset from the reference (GPS) time;

[math]\displaystyle{ c }[/math] is the vacuum speed of light;

[math]\displaystyle{ Tr }[/math] is the signal path delay due to the troposphere;

[math]\displaystyle{ \lambda }[/math] is the carrier combination wavelength;

[math]\displaystyle{ N }[/math] is the ambiguity of the carrier-phase ionosphere-free combination (it is not an integer number);

[math]\displaystyle{ \varepsilon_P }[/math] and [math]\displaystyle{ \varepsilon_\phi }[/math] are the measurement noise components, including multipath and other effects;

[math]\displaystyle{ \rho }[/math] is the geometrical range between the satellite and the receiver, computed as a function of the satellite [math]\displaystyle{ (x_{Sat}, y_{Sat},z_{Sat}) }[/math] and receiver [math]\displaystyle{ (x_{Rx}, y_{Rx},z_{Rx}) }[/math] coordinates as:

[math]\displaystyle{ \rho=\sqrt{〖(x_{Sat}-x_{Rx})〗^2+〖(y_{Sat}-y_{Rx})〗^2+〖(z_{Sat}-z_{Rx})〗^2 } \qquad \mbox{(3)} }[/math].

The observations coming from all the satellites are processed together in a filter that solves for the different unknowns, namely the receiver coordinates, the receiver clock, the zenith tropospheric delay and the phase ambiguities.

Most implementations of PPP algorithms use a sequential filter in which the process noise for the coordinates is adjusted depending on the receiver dynamics, the time evolution of the clock is more or less unconstrained (white noise with a high sigma), and the process noise for the tropospheric delay is adjusted to standard tropospheric activity. In the case of phase ambiguities, they are considered as a constant per pass.

Other implementations feature a batch algorithm instead, and therefore no process noise has to be modeled. In this case, the receiver clock offset is estimated at every measurement epoch, the coordinates are adjusted for all the observation interval (static mode) or per epoch (kinematic mode), the troposphere is estimated at regular fixed intervals and the ambiguities are also estimated per pass.

The slant tropospheric delay Tr is expressed as a function of the zenith delay (which is the parameter that is actually estimated in PPP) through the use of a mapping function. The precise modeling of Earth dynamics (causing variations of the static receiver coordinates with respect to the terrestrial reference frame) is normally based on the International Earth Rotation and Reference Systems Service(IERS) recommendations. Such models can include solid Earth tides, ocean loading and Earth Rotation. The modeling of the observables includes for instance the offset between the antenna phase center and the satellite center of mass, and the so-called phase wind-up at the receiver.

Static PPP Performances at GSLV IGS station (static mode)

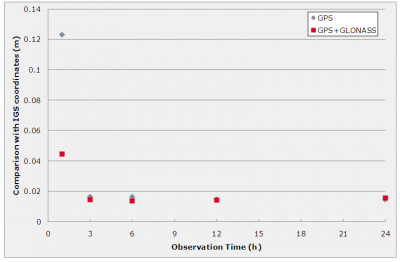
The accuracy of the satellite clocks and orbits is one of the most important factors affecting the quality of the PPP Solution. Normally, the International GNSS Service (IGS) products are used due to their high accuracy; however the IGS does not currently provide GLONASS clocks. Furthermore, IGS products have a latency of several hours, which makes them not valid for real-time PPP. Another relevant factor that affects the PPP performances is the amount (number of satellites in view at each epoch) and quality (noise, multipath) of the observations. For instance, more satellites in view improve the observability of the zenith tropospheric delay. Therefore, a possible way to increase the reliability of this technique is to process GPS and GLONASS observations together. Given that PPP is not a differential technique, it cannot resolve carrier phase ambiguities and they need to be estimated with the aid of the code measurements. This fact makes the convergence period longer than in other techniques (RTK, for instance), thus requiring longer observation times for static positioning.

The positioning performances of the PPP technique are directly related to the accuracy of the reference GNSS orbit and clock products. Usually the accuracy of the offline PPP solution (vs. the coordinates published by the IGS) is around 1 cm. To enable a real time positioning service, the generation of precise satellite orbits and clocks in real time becomes a major challenge; the IGS Real Time Pilot Project is the official project to move towards real-time GNSS data and derived products. An important theme of the pilot project will be to support and promote the development of real-time applications, as Real-Time PPP.