Perturbed Motion

Fundamentals
Title	Perturbed Motion
Author(s)	J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain.
Level	Medium
Year of Publication	2011

The two-body problem is only a first approximation to the real case. In practice, an additional set of accelerations or disturbing terms, must be added due to:

1. Non-sphericity of the Earth and non-homogeneous mass distribution:

As commented before, the shape of the Earth can be approximated by an ellipsoid, with equatorial radius about [math]\displaystyle{ 20\,km }[/math] larger than polar radius. On the other hand, the density is not uniform and the gravitational force depends on the latitude and longitude besides the radial distance. Thus, the Earth potential can be represented by a spherical harmonic expansion [Hofmann-Wellenhof et al., 2008] like:

[math]\displaystyle{ \begin{array}{ll} V= & \frac{\mu}{r}\left[ 1- \displaystyle \sum_{n=2}^{\infty}{\left(\frac{a_e}{r}\right)^n J_n\; P_n(\sin \phi)} \right .\\ & + \left. \sum_{n=2}^{\infty}{\displaystyle \sum_{m=1}^{\infty}{\left(\frac{a_e}{r}\right)^n \left[ C_{nm} \cos m\lambda + S_{nm} \sin m\lambda \right ] P_{nm}(\sin \phi)}}\right ] \end{array} \qquad \mbox{(1)} }[/math]

where [math]\displaystyle{ a_e }[/math] is the semi-major axis of the Earth, [math]\displaystyle{ r }[/math] is the geocentric distance of the satellite, and [math]\displaystyle{ \phi }[/math], [math]\displaystyle{ \lambda }[/math] are its latitude and longitude. The parameters [math]\displaystyle{ J_n }[/math], [math]\displaystyle{ C_{nm} }[/math], [math]\displaystyle{ S_{nm} }[/math] denote the zonal ([math]\displaystyle{ m=0 }[/math]) and tesseral ([math]\displaystyle{ m \neq 0 }[/math]) coefficients of the harmonic development known from an Earth model. [math]\displaystyle{ P_n }[/math] and [math]\displaystyle{ P_{nm} }[/math] are the Legendre polynomials and the associated Legendre functions, respectively.

The even-degree zonal coefficients produce primary secular variations of the orbital parameters, and the odd-degree zonal produce long-period perturbations. The tesseral coefficients produce short -periodic perturbations.

The term with coefficient [math]\displaystyle{ J_2 }[/math] in (1), the harmonic coefficient of second order and degree zero, essentially models the ellipsoidal shape of the Earth (with homogeneous density). It is smaller, by a factor of [math]\displaystyle{ 10^4 }[/math], than the acceleration due to the spherical Earth with uniform density (i.e., [math]\displaystyle{ \nabla (\mu/r)=-\frac{\mu}{r^3}r }[/math]). On the other hand, this term is approximately three orders of magnitude larger than the other coefficients (see table 3). Taking only this term in the potential, the previous expression becomes:

[math]\displaystyle{ V(r,\phi,\lambda)=\frac{\mu}{r}\left[1+\frac{1}{2}\left(\frac{a_e}{r}\right)^2 J_2\;\;(1-3\sin^2 \phi) \right] \qquad \mbox{(2)} }[/math]

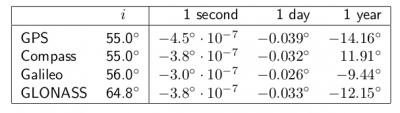
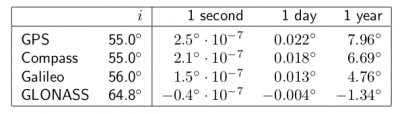
The oblateness of the Earth ([math]\displaystyle{ J_2 }[/math]) produces two effects: First, a torque which rotates the satellite's orbit in the equatorial plane, producing a nodal regression [math]\displaystyle{ \frac{d \Omega}{dt} }[/math]. This is a secular effect (i.e., timely cumulative) which depends upon the inclination of the orbit. It is zero for a polar orbit and maximum for an equatorial orbit. Next table (from [Cojocaru, 2009] ) shows the rate of change for the GPS, Galileo and GLONASS satellites.

Table 1: Secular precession of GNSS ascending node produced by [math]\displaystyle{ J_2 }[/math].

The second effect of the non-central geo-potential ([math]\displaystyle{ J_2 }[/math]) produces a rotation of the perigee [math]\displaystyle{ \frac{d \omega}{dt} }[/math] (i.e., a rotation of the major axis in the orbital plane).

Table 2: Secular precession of GNSS perigee produced by [math]\displaystyle{ J_2 }[/math].

This second harmonic of the geopotential ([math]\displaystyle{ J_2 }[/math]) does not produce secular perturbations in the elements [math]\displaystyle{ a }[/math], [math]\displaystyle{ e }[/math] and [math]\displaystyle{ i }[/math].

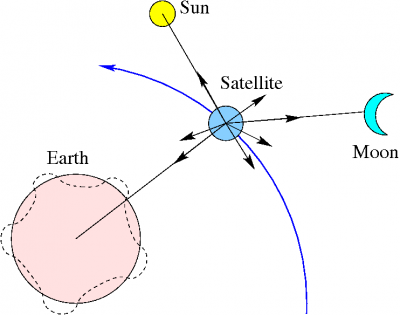
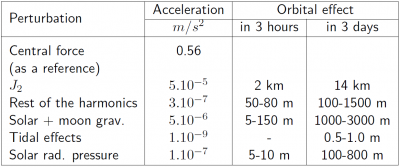
2. The presence of other celestial bodies, foremost, the sun and the moon:The gravitational field of sun and moon act as perturbing forces on the satellites, being the moon the body producing the largest effects . These gravitational forces also produce tides deforming the shape of the Earth and affecting its gravitational potential. Nevertheless, these tidal effects produce on GNSS satellites accelerations at the order of [math]\displaystyle{ 10^{-9} m/s^2 }[/math], which are three orders of magnitude lower than the moon and solar gravitational acceleration (see table \ref{tab:perturb}).

3. Solar radiation pressure:This is produced by the photons impacting on the satellite surface and mainly depends on the reflective properties and the area-to-mass ratio of the satellite. It also depends on an eclipse factor, being zero when the satellite is in the Earth's shadow. The effect of solar radiation pressure on a satellite orbit is very difficult to model, and some contribution is estimated as stochastic acceleration parameters in the filter during the orbit estimation.

Note that although the sun and the moon gravitational effects and the non-gravitational solar radiation pressure perturbing accelerations appear very small, their accumulated effect can produce significant changes in the GNSS satellites orbits over a large period of time. Table 3 (from [Seeber, 1993] ) shows the different perturbation magnitudes and their effect over GPS orbits.

Figure 1: Perturbations over the satellite orbit.

Table 3: Different perturbation magnitudes, and their effects on GPS orbits.