If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Pole Tide: Difference between revisions
Jaume.Sanz (talk | contribs) No edit summary |
Jaume.Sanz (talk | contribs) No edit summary |
||
| Line 37: | Line 37: | ||
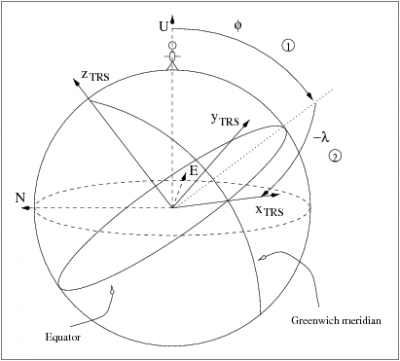
The displacement <math>\displaystyle \delta</math> is given in the radial, longitude and latitude <math>(\hat{\mathbf r}, \hat{\boldsymbol \lambda}, \hat{\boldsymbol \varphi})</math> vectors, i.e., the North | The displacement <math>\displaystyle \delta</math> is given in the radial, longitude and latitude <math>(\hat{\mathbf r}, \hat{\boldsymbol \lambda}, \hat{\boldsymbol \varphi})</math> vectors, i.e., the Up East North (UEN) local system, and, thence, can be transformed to the TRS reference system (see [[Reference Frames in GNSS]]) applying the following latitude and longitude rotations indicated in figure 1: | ||
| Line 65: | Line 65: | ||
::[[File:Pole_Tide_UEN2CTS.png|none|thumb|400px|'''''Figure 1:''''' Transformation from | ::[[File:Pole_Tide_UEN2CTS.png|none|thumb|400px|'''''Figure 1:''''' Transformation from UEN <math>(\hat{\mathbf r}, \hat{\boldsymbol \lambda}, \hat{\boldsymbol \varphi})</math> to TRS <math>(x,y,x)</math> coordinates.]] | ||
Revision as of 10:37, 8 February 2012
| Fundamentals | |
|---|---|
| Title | Pole Tide |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
The instantaneous earth rotation axis shifts inside a square of about [math]\displaystyle{ 20 }[/math] meters in relation to a point with fixed coordinates on the earth (i.e., Chandler wobble with a period of [math]\displaystyle{ 14 }[/math] months). This entails a varying elastic response of the earth's crust. This has an effect smaller than [math]\displaystyle{ 2.5 }[/math] centimetres in vertical and [math]\displaystyle{ 0.7 }[/math] centimetres in horizontal, but must be taken into account if the observations are carried out over periods longer than two months.
From the IERS Conventions [Denis et al., 2004] [1], pages 83-84, the following expression [footnotes 1] can be derived for the displacement at a point of geographic latitude [math]\displaystyle{ \displaystyle \varphi }[/math] and longitude [math]\displaystyle{ \displaystyle \lambda }[/math]:
- [math]\displaystyle{ \begin{array}{ll} \delta_{\hat{\mathbf r}}=&-\frac{\omega^2_E \, R^2}{2\,g}\,h \, \sin 2\varphi \left ( m_1 \cos \lambda + m_2 \sin \lambda \right ) \,\hat {\mathbf r}\qquad \\[0.3cm] \delta_{\hat{\mathbf \lambda}}= & -\frac{\omega^2_E \, R^2}{g}\, l \, \sin \varphi \left (-m_1 \sin \lambda + m_2 \cos \lambda \right ) \, \hat{\mathbf \lambda} \qquad \\[0.3cm] \delta_{\hat{\mathbf \varphi}}= & -\frac{\omega^2_E \, R^2}{g}\, l\, \cos 2\varphi \left (\, m_1 \cos \lambda + m_2 \sin \lambda \right )\, \hat{\mathbf \varphi}\qquad \end{array} \qquad\mbox{(1)} }[/math]
where ([math]\displaystyle{ \displaystyle m_1 }[/math],[math]\displaystyle{ \displaystyle m_2 }[/math]) are the displacements from the 1903.0 CIO, pole position, and [math]\displaystyle{ \displaystyle h= 0.6027 }[/math], [math]\displaystyle{ \displaystyle l=0.0836 }[/math] are the Love numbers.
Taking the earth's angular rotation [math]\displaystyle{ \omega_E= 7.29\cdot 10^{-5} }[/math], the earth's equatorial radius [math]\displaystyle{ R=6378\, km }[/math] and the gravitational acceleration [math]\displaystyle{ g=9.8\, m/sec^2 }[/math], it follows:
- [math]\displaystyle{ \begin{array}{ll} \delta_{\hat{\mathbf r}}=&-32 \, \sin 2\varphi \left ( m_1 \cos \lambda + m_2 \sin \lambda \right ) \, \hat {\mathbf r}\qquad \mbox{(mm)} \\[0.3cm] \delta_{\hat{\mathbf \lambda}}= & -9 \, \sin \varphi \left (-m_1 \sin \lambda + m_2 \cos \lambda \right ) \, \hat{\mathbf \lambda} \qquad \mbox{(mm)} \\[0.3cm] \delta_{\hat{\mathbf \varphi}}= & -9 \, \cos 2\varphi \left (\, m_1 \cos \lambda + m_2 \sin \lambda \right )\, \hat{\mathbf \varphi}\qquad \mbox{(mm)} \end{array} \qquad\mbox{(2)} }[/math]
where ([math]\displaystyle{ \displaystyle m_1 }[/math],[math]\displaystyle{ \displaystyle m_2 }[/math]) are the displacements (given in seconds of arc). Pole displacements can be found at ftp://hpiers.obspm.fr/iers/eop/eop.others.
The displacement [math]\displaystyle{ \displaystyle \delta }[/math] is given in the radial, longitude and latitude [math]\displaystyle{ (\hat{\mathbf r}, \hat{\boldsymbol \lambda}, \hat{\boldsymbol \varphi}) }[/math] vectors, i.e., the Up East North (UEN) local system, and, thence, can be transformed to the TRS reference system (see Reference Frames in GNSS) applying the following latitude and longitude rotations indicated in figure 1:
- [math]\displaystyle{ \left[ \begin{array}{c} \Delta x \\ \Delta y \\ \Delta z \end{array} \right]= \underbrace{\left( \begin{array}{ccc} \cos \lambda \cos \varphi & -\sin \lambda & -\cos \lambda \sin \varphi \\ \sin \lambda \cos \varphi & \cos \lambda & -\sin \lambda \sin \varphi \\ \sin \varphi & 0 & \cos \Phi \end{array} \right)}_{{\mathbf R}_3(-\lambda )\cdot {\mathbf R}_2(\varphi )} \left[ \begin{array}{l} \delta_{\hat{\mathbf r}}\\ \delta_{\hat{\mathbf \lambda}}\\ \delta_{\hat{\mathbf \varphi}} \end{array} \right] \qquad\mbox{(2)} }[/math]
Notes
- ^ Notice the use of latitude [math]\displaystyle{ \displaystyle \varphi }[/math] in equations (1 and 2), instead of the co-latitude [math]\displaystyle{ \displaystyle \theta }[/math] used in the IERS equations.
References
- ^ [Denis et al., 2004] Denis, D., McCarthy and Petit, G., 2004. IERS Conventions (2003). IERS Technical Note 32.. IERS Convention Center., Frankfurt am Main.