If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
GLONASS Satellite Coordinates Computation: Difference between revisions
Carlos.Lopez (talk | contribs) No edit summary |
Carlos.Lopez (talk | contribs) No edit summary |
||
| (27 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{{Article Infobox2 | {{Article Infobox2 | ||
|Category=Fundamentals | |Category=Fundamentals | ||
|Authors=J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. | |||
|Level=Intermediate | |||
|YearOfPublication=2011 | |||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
The [[GLONASS General Introduction|GLONASS]] satellite coordinates shall be computed according to the specifications in the [[GLONASS General Introduction|GLONASS]]-ICD document. An accuracy level of about three meters can be reached using the algorithm provided by this ICD. | |||
In table 1 are listed the broadcast ephemeris parameters which are used to compute [[GLONASS General Introduction|GLONASS]] satellites coordinates. Essentially, the ephemeris contain the initial conditions of position and velocity to perform the numerical integration of the [[GLONASS General Introduction|GLONASS]] orbit within the interval of measurement <math>|t - t_e| < 15</math> minutes. The accelerations due solar and lunar gravitational perturbations are also given. | |||
In | |||
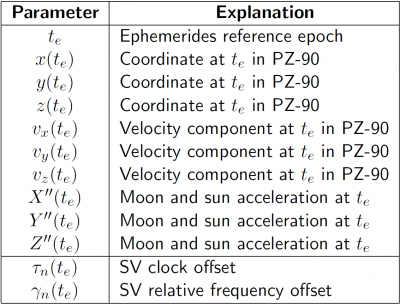
::[[File: GLONASS_SV_Coord_Comp.png|none|thumb|400px|'''''Table 1:''''' GLONASS broadcast ephemeris and clock message parameters.]] | ::[[File: GLONASS_SV_Coord_Comp.png|none|thumb|400px|'''''Table 1:''''' GLONASS broadcast ephemeris and clock message parameters.]] | ||
In order to compute PZ-90 [[GLONASS]] satellite coordinates from the navigation message, the following algorithm must be used [GLONASS ICD, 1998] <ref> [GLONASS ICD, 1998] GLONASS ICD, 1998. Technical report. v.4.0.</ref>. | In order to compute PZ-90 [[GLONASS General Introduction|GLONASS]] satellite coordinates from the navigation message, the following algorithm must be used [GLONASS ICD, 1998] <ref> [GLONASS ICD, 1998] GLONASS ICD, 1998. Technical report. v.4.0.</ref>. | ||
| Line 24: | Line 22: | ||
::*''' 1. Coordinates transformation to an inertial reference frame:''' | ::*''' 1. Coordinates transformation to an inertial reference frame:''' | ||
:::- The initial conditions <math>(x(t_e),y(t_e),z(t_e),v_x(t_e),v_y(t_e),v_z(t_e))</math>, as broadcast in the [[GLONASS]] navigation message, are in the ECEF Greenwich coordinate system PZ-90. Therefore, and previous to orbit integration, they must be transformed to an absolute (inertial) coordinate system using the following expressions <ref group="footnotes"> Note: Over a small integration intervals, a simple rotation of <math>\theta_{G_e}</math> angle around Z-axis is enough to perform this transformation. Nutation and precession of the earth and polar motion are a very slow | :::- The initial conditions <math>(x(t_e),y(t_e),z(t_e),v_x(t_e),v_y(t_e),v_z(t_e))</math>, as broadcast in the [[GLONASS General Introduction|GLONASS]] navigation message, are in the ECEF Greenwich coordinate system PZ-90. Therefore, and previous to orbit integration, they must be transformed to an absolute (inertial) coordinate system using the following expressions <ref group="footnotes"> Note: Over a small integration intervals, a simple rotation of <math>\theta_{G_e}</math> angle around Z-axis is enough to perform this transformation. Nutation and precession of the earth and polar motion are a very slow processes and will not introduce significant deviations on such short integration time intervals (see [[Transformation between Celestial and Terrestrial Frames]]).</ref>: | ||
::::'''Position:''' | ::::'''Position:''' | ||
| Line 68: | Line 66: | ||
:::being: | :::being: | ||
:::- <math>\omega_E</math>: | :::- <math>\omega_E</math>: earth's rotation rate (<math>0.7292115\, 10^{-4}\; rad/s</math>)). | ||
:::- <math>\theta_{G_0}</math>: the sidereal time in Greenwich at midnight GMT of a date at which the epoch <math>t_e</math> is specified. (Notice: GLONASS_time | :::- <math>\theta_{G_0}</math>: the sidereal time in Greenwich at midnight GMT of a date at which the epoch <math>t_e</math> is specified. (Notice: GLONASS_time = UTC(SU) + <math>3</math> hours). | ||
::*''' 2. Numerical integration of differential equations that describe the motion of the satellites.''' | ::*''' 2. Numerical integration of differential equations that describe the motion of the satellites.''' | ||
:::According to [[GLONASS]]-ICD, the re-calculation of ephemeris from epoch <math>t_e</math> to epoch <math>t_i</math> within the interval | :::According to [[GLONASS General Introduction|GLONASS]]-ICD, the re-calculation of ephemeris from epoch <math>t_e</math> to epoch <math>t_i</math> within the measurement interval (<math>|t_i-t_e|<15 min</math>) shall be performed by a numerical integration of the differential equations (5) describing the motion of the satellites. These equations shall be integrated in a direct absolute geocentric coordinate system OXa, OYa, OZa, connected with current equator and vernal equinox, using the 4th order Runge-Kutta technique: | ||
:::::<math> | :::::<math> | ||
| Line 92: | Line 90: | ||
:::where: | :::where: | ||
:::::<math>\bar{\mu}=\frac{\mu}{r^2}</math>,<math>\bar{x_a}=\frac{x_a}{r}</math>, <math>\bar{y_a}=\frac{y_a}{r}</math>, math>\bar{z_a}=\frac{x_a}{r}</math>, <math>\bar{\rho}=\frac{a_E}{r}</math>, <math>r=\sqrt{x_a^2+y_a^2+z_a^2}</math> | :::::<math>\bar{\mu}=\frac{\mu}{r^2}</math>,<math>\bar{x_a}=\frac{x_a}{r}</math>, <math>\bar{y_a}=\frac{y_a}{r}</math>, <math>\bar{z_a}=\frac{x_a}{r}</math>, <math>\bar{\rho}=\frac{a_E}{r}</math>, <math>r=\sqrt{x_a^2+y_a^2+z_a^2}</math> | ||
:::::<math>a_E= 6\,378.136\; km</math> | :::::<math>a_E= 6\,378.136\; km</math> Equatorial radius of the Earth (PZ-90). | ||
:::::<math>\mu= 398\,600.44\; km^3/s^2</math> | :::::<math>\mu= 398\,600.44\; km^3/s^2</math> Gravitational constant (PZ-90). | ||
:::::<math>C_{20}=-1\,082.63\cdot 10^{-6}</math> | :::::<math>C_{20}=-1\,082.63\cdot 10^{-6}</math> Second zonal coefficient of spherical harmonic expression. | ||
:::''Note'': In the above differential equations system (5), the term <math>C_{20}=-J_2=+\sqrt{5}\bar{C}_{20}</math> is used instead of <math>J_2</math> in equations <math> | :::''Note'': In the above differential equations system (5), the term <math>C_{20}=-J_2=+\sqrt{5}\bar{C}_{20}</math> is used instead of <math>J_2</math> in equations <math> | ||
V(r,\phi,\lambda)=\frac{\mu}{r}\left[1+\frac{1}{2}\left(\frac{a_e}{r}\right)^2 J_2\;\;(1-3\sin^2 \phi) \right] </math> and <math> \mathbb{\mathbf {\ddot r}}=\nabla V+\mathbb{\mathbf k}_{sun\_moon} </math> to keep the same expressions as in the [[GLONASS]]-ICD (please refer to [[Perturbed Motion]] and [[GNSS Broadcast Orbits]]) | V(r,\phi,\lambda)=\frac{\mu}{r}\left[1+\frac{1}{2}\left(\frac{a_e}{r}\right)^2 J_2\;\;(1-3\sin^2 \phi) \right] </math> and <math> \mathbb{\mathbf {\ddot r}}=\nabla V+\mathbb{\mathbf k}_{sun\_moon} </math> to keep the same expressions as in the [[GLONASS General Introduction|GLONASS]]-ICD (please refer to [[Perturbed Motion]] and [[GNSS Broadcast Orbits]]) | ||
:::The right-hand side of the previous equation system (5) takes into account the accelerations determined by the central body gravitational constant <math>\mu</math>, the second zonal coefficient <math>C_{20}</math> (that characterises polar flattening of | :::The right-hand side of the previous equation system (5) takes into account the accelerations determined by the central body gravitational constant <math>\mu</math>, the second zonal coefficient <math>C_{20}</math> (that characterises polar flattening of the Earth), and the accelerations due to the luni-solar gravitational perturbation. | ||
| Line 132: | Line 130: | ||
\begin{array}{l} | \begin{array}{l} | ||
\mathbb{\mathbf K}_1= \mathbb{\mathbf F}(t_n,\mathbb{\mathbf Y}_n)\\ | \mathbb{\mathbf K}_1= \mathbb{\mathbf F}(t_n,\mathbb{\mathbf Y}_n)\\ | ||
\mathbb{\mathbf K}_2= \mathbb{\mathbf F}(t_n+h/2,\mathbb{\mathbf Y}_n+\mathbb{\mathbf K}_1/2)\\ | \mathbb{\mathbf K}_2= \mathbb{\mathbf F}(t_n+h/2,\mathbb{\mathbf Y}_n+h \mathbb{\mathbf K}_1/2)\\ | ||
\mathbb{\mathbf K}_3= \mathbb{\mathbf F}(t_n+h/2,\mathbb{\mathbf Y}_n+\mathbb{\mathbf K}_2/2)\\ | \mathbb{\mathbf K}_3= \mathbb{\mathbf F}(t_n+h/2,\mathbb{\mathbf Y}_n+h \mathbb{\mathbf K}_2/2)\\ | ||
\mathbb{\mathbf K}_4= \mathbb{\mathbf F}(t_n+h,\mathbb{\mathbf Y}_n+\mathbb{\mathbf K}_3)\\ | \mathbb{\mathbf K}_4= \mathbb{\mathbf F}(t_n+h,\mathbb{\mathbf Y}_n+h \mathbb{\mathbf K}_3)\\ | ||
\mathbb{\mathbf Y}_{n+1}=\mathbb{\mathbf Y}_n+\mathbb{\mathbf K}_1 | \mathbb{\mathbf Y}_{n+1}=\mathbb{\mathbf Y}_n+h/6(\mathbb{\mathbf K}_1+2\mathbb{\mathbf K}_2+2\mathbb{\mathbf K}_3+\mathbb{\mathbf K}_4+ O(h^5)\\ | ||
\end{array} \qquad \mbox{(7)} | \end{array} \qquad \mbox{(7)} | ||
</math> | </math> | ||
:::The method is initialised with the initial conditions <math>\mathbb{\mathbf Y}(t_0)</math> and <math>\mathbb{\mathbf Y}'(t_0)</math>. For the numerical integration of [[GLONASS]] satellite orbits, the function <math>\mathbb{\mathbf F}(t,\mathbb{\mathbf Y})</math> is given by (7). | :::The method is initialised with the initial conditions <math>\mathbb{\mathbf Y}(t_0)</math> and <math>\mathbb{\mathbf Y}'(t_0)</math>. For the numerical integration of [[GLONASS General Introduction|GLONASS]] satellite orbits, the function <math>\mathbb{\mathbf F}(t,\mathbb{\mathbf Y})</math> is given by (7). | ||
::*''' 3. Coordinates transformation back to the PZ-90 reference system:''' | ::*''' 3. Coordinates transformation back to the PZ-90 reference system:''' | ||
:::The coordinates <math>(x(t), y(t), z(t))</math>, obtained from the motion equations numerical integration, shall be transformed back to the | :::The coordinates <math>(x(t), y(t), z(t))</math>, obtained from the motion equations numerical integration, shall be transformed back to the Earth fixed reference frame PZ-90 with the following equations: | ||
:::::<math> | :::::<math> | ||
| Line 155: | Line 153: | ||
::: | :::where <math>\theta_G</math> is the sidereal time at Greenwich meridian at time <math>t</math>, where <math>t</math> is in GLONASS time, see equation (4) : | ||
:::::<math> | :::::<math> | ||
| Line 166: | Line 164: | ||
:::Note that [[GLONASS]] satellite coordinates are computed in PZ-90 reference system, instead of WGS-84 where the GPS coordinates have been calculated. To bring the PZ-90 coordinate system in coincidence with WGS-84 the transformation given by equation (11) must be applied (see [[Reference Frames in GNSS]]): | :::Note that [[GLONASS General Introduction|GLONASS]] satellite coordinates are computed in PZ-90 reference system, instead of WGS-84 where the GPS coordinates have been calculated. To bring the PZ-90 coordinate system in coincidence with WGS-84 the transformation given by equation (11) must be applied (see [[Reference Frames in GNSS]]): | ||
:::::<math> | :::::<math> | ||
| Line 210: | Line 208: | ||
:::The transformation from PZ-90.02 to WGS-84 (actually ITRF2000) is given by <math>\Delta x= -0.36\,m</math>, <math>\Delta y= +0.08\, m</math>, <math>\Delta z= +0.18\, m</math>, with no rotation, i.e., equation (12) was implemented in September 20th 2007 at 18:00. (refer to [[Reference Frames in GNSS]]): | :::The transformation from PZ-90.02 to WGS-84 (actually ITRF2000) is given by <math>\Delta x= -0.36\,m</math>, <math>\Delta y= +0.08\, m</math>, <math>\Delta z= +0.18\, m</math>, with no rotation, i.e., equation (12)<ref group="footnotes"> The PZ-90.02 was implemented in September 20th, 2007 at 18:00. (refer to [[Reference Frames in GNSS]]).</ref>: | ||
:::::<math> | :::::<math> | ||
Latest revision as of 10:16, 23 February 2012
| Fundamentals | |
|---|---|
| Title | GLONASS Satellite Coordinates Computation |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
The GLONASS satellite coordinates shall be computed according to the specifications in the GLONASS-ICD document. An accuracy level of about three meters can be reached using the algorithm provided by this ICD.
In table 1 are listed the broadcast ephemeris parameters which are used to compute GLONASS satellites coordinates. Essentially, the ephemeris contain the initial conditions of position and velocity to perform the numerical integration of the GLONASS orbit within the interval of measurement [math]\displaystyle{ |t - t_e| \lt 15 }[/math] minutes. The accelerations due solar and lunar gravitational perturbations are also given.
In order to compute PZ-90 GLONASS satellite coordinates from the navigation message, the following algorithm must be used [GLONASS ICD, 1998] [1].
Computation equations and algorithm
- 1. Coordinates transformation to an inertial reference frame:
- - The initial conditions [math]\displaystyle{ (x(t_e),y(t_e),z(t_e),v_x(t_e),v_y(t_e),v_z(t_e)) }[/math], as broadcast in the GLONASS navigation message, are in the ECEF Greenwich coordinate system PZ-90. Therefore, and previous to orbit integration, they must be transformed to an absolute (inertial) coordinate system using the following expressions [footnotes 1]:
- Position:
- [math]\displaystyle{ \begin{array}{l} x_a(t_e)=x(t_e) \cos(\theta_{G_e}) - y(t_e) \sin (\theta_{G_e}) \\ y_a(t_e)=x(t_e) \sin(\theta_{G_e}) + y(t_e) \cos(\theta_{G_e}) \\ z_a(t_e)=z(t_e) \\ \end{array} \qquad \mbox{(1)} }[/math]
- Position:
- Velocity:
- [math]\displaystyle{ \begin{array}{l} v_{x_a}(t_e)=v_x(t_e) \cos(\theta_{G_e}) - v_y(t_e) \sin (\theta_{G_e})- \omega_E \; y_a(t_e) \\ v_{y_a}(t_e)=v_x(t_e) \sin(\theta_{G_e}) + v_y(t_e) \cos(\theta_{G_e})+\omega_E \; x_a(t_e) \\ v_{z_a}(t_e)=v_z(t_e) \\ \end{array} \qquad \mbox{(2)} }[/math]
- Velocity:
- - The [math]\displaystyle{ \left( X''(t_e),Y''(t_e),Z''(t_e) \right) }[/math] acceleration components broadcast in the navigation message are the projections of luni-solar accelerations to axes of the ECEF Greenwich coordinate system. Thence, these accelerations must be transformed to the inertial system by:
- [math]\displaystyle{ \begin{array}{l} (Jx_am+Jx_as)=X''(t_e) \cos(\theta_{G_e}) -Y''(t_e) \sin(\theta_{G_e})\\ (Jx_am+Jx_as)=X''(t_e) \sin(\theta_{G_e}) +Y''(t_e) \cos(\theta_{G_e})\\ (Jx_am+Jx_as)=Z''(t_e)\\ \end{array} \qquad \mbox{(3)} }[/math]
- Where [math]\displaystyle{ (\theta_{G_e}) }[/math] is the sidereal time at epoch [math]\displaystyle{ t_e }[/math], to which are referred the initial conditions, in Greenwich meridian:
- [math]\displaystyle{ \theta_{G_e}= \theta_{G_0} + \omega_E (t_e-3\, hours) \qquad \mbox{(4)} }[/math]
- Where [math]\displaystyle{ (\theta_{G_e}) }[/math] is the sidereal time at epoch [math]\displaystyle{ t_e }[/math], to which are referred the initial conditions, in Greenwich meridian:
- being:
- - [math]\displaystyle{ \omega_E }[/math]: earth's rotation rate ([math]\displaystyle{ 0.7292115\, 10^{-4}\; rad/s }[/math])).
- - [math]\displaystyle{ \theta_{G_0} }[/math]: the sidereal time in Greenwich at midnight GMT of a date at which the epoch [math]\displaystyle{ t_e }[/math] is specified. (Notice: GLONASS_time = UTC(SU) + [math]\displaystyle{ 3 }[/math] hours).
- 2. Numerical integration of differential equations that describe the motion of the satellites.
- According to GLONASS-ICD, the re-calculation of ephemeris from epoch [math]\displaystyle{ t_e }[/math] to epoch [math]\displaystyle{ t_i }[/math] within the measurement interval ([math]\displaystyle{ |t_i-t_e|\lt 15 min }[/math]) shall be performed by a numerical integration of the differential equations (5) describing the motion of the satellites. These equations shall be integrated in a direct absolute geocentric coordinate system OXa, OYa, OZa, connected with current equator and vernal equinox, using the 4th order Runge-Kutta technique:
- [math]\displaystyle{ \left\{ \begin{array}{l} \frac{dx_a}{dt}=v_{x_a}(t)\\ \frac{dy_a}{dt}=v_{y_a}(t)\\ \frac{dz_a}{dt}=v_{z_a}(t)\\ \frac{dv_{x_a}}{dt}=-\bar{\mu} \bar{x}_a +\frac{3}{2}C_{20}\bar{\mu} \bar{x}_a \rho^2(1-5 \bar{z}_a^2)+ Jx_am+Jx_as\\ \frac{dv_{y_a}}{dt}=-\bar{\mu} \bar{y}_a +\frac{3}{2}C_{20}\bar{\mu} \bar{y}_a \rho^2(1-5 \bar{z}_a^2)+ Jx_am+Jx_as\\ \frac{dv_{z_a}}{dt}=-\bar{\mu} \bar{z}_a +\frac{3}{2}C_{20}\bar{\mu} \bar{z}_a \rho^2(3-5 \bar{z}_a^2)+ Jx_am+Jx_as\\ \end{array} \qquad \mbox{(5)} \right . }[/math]
- where:
- [math]\displaystyle{ \bar{\mu}=\frac{\mu}{r^2} }[/math],[math]\displaystyle{ \bar{x_a}=\frac{x_a}{r} }[/math], [math]\displaystyle{ \bar{y_a}=\frac{y_a}{r} }[/math], [math]\displaystyle{ \bar{z_a}=\frac{x_a}{r} }[/math], [math]\displaystyle{ \bar{\rho}=\frac{a_E}{r} }[/math], [math]\displaystyle{ r=\sqrt{x_a^2+y_a^2+z_a^2} }[/math]
- [math]\displaystyle{ a_E= 6\,378.136\; km }[/math] Equatorial radius of the Earth (PZ-90).
- [math]\displaystyle{ \mu= 398\,600.44\; km^3/s^2 }[/math] Gravitational constant (PZ-90).
- [math]\displaystyle{ C_{20}=-1\,082.63\cdot 10^{-6} }[/math] Second zonal coefficient of spherical harmonic expression.
- Note: In the above differential equations system (5), the term [math]\displaystyle{ C_{20}=-J_2=+\sqrt{5}\bar{C}_{20} }[/math] is used instead of [math]\displaystyle{ J_2 }[/math] in equations [math]\displaystyle{ V(r,\phi,\lambda)=\frac{\mu}{r}\left[1+\frac{1}{2}\left(\frac{a_e}{r}\right)^2 J_2\;\;(1-3\sin^2 \phi) \right] }[/math] and [math]\displaystyle{ \mathbb{\mathbf {\ddot r}}=\nabla V+\mathbb{\mathbf k}_{sun\_moon} }[/math] to keep the same expressions as in the GLONASS-ICD (please refer to Perturbed Motion and GNSS Broadcast Orbits)
- The right-hand side of the previous equation system (5) takes into account the accelerations determined by the central body gravitational constant [math]\displaystyle{ \mu }[/math], the second zonal coefficient [math]\displaystyle{ C_{20} }[/math] (that characterises polar flattening of the Earth), and the accelerations due to the luni-solar gravitational perturbation.
- Runge-Kutta integration algorithm
- Given the following initial value problem:
- [math]\displaystyle{ \left\{ \begin{array}{c} \frac{dy_1}{dt}=f_1(t,y_1,\cdots,y_n)\\ \vdots\\ \frac{dy_n}{dt}=f_1(t,y_1,\cdots,y_n)\\ \end{array} \right . \Longleftrightarrow \mathbb{\mathbf Y}'(t)=\mathbb{\mathbf F}(t,\mathbb{\mathbf Y}(t)) \qquad \mbox{(6)} }[/math]
- [math]\displaystyle{ \mathbb{\mathbf Y}(t_0)=[y_1(t_0), \cdots, y_n(t_0)]^T }[/math], [math]\displaystyle{ \mathbb{\mathbf Y'}(t_0)=[y'_1(t_0), \cdots, y'_n(t_0)]^T }[/math]
- It is desired to find the [math]\displaystyle{ \mathbb{\mathbf Y}(t_f) }[/math] at some final time [math]\displaystyle{ t_f }[/math], or [math]\displaystyle{ \mathbb{\mathbf Y}(t_k) }[/math] at some discrete list of points [math]\displaystyle{ t_k }[/math] (for example, at tabulated intervals).
- The Runge-Kutta method is based in the following algorithm:
- [math]\displaystyle{ \begin{array}{l} \mathbb{\mathbf K}_1= \mathbb{\mathbf F}(t_n,\mathbb{\mathbf Y}_n)\\ \mathbb{\mathbf K}_2= \mathbb{\mathbf F}(t_n+h/2,\mathbb{\mathbf Y}_n+h \mathbb{\mathbf K}_1/2)\\ \mathbb{\mathbf K}_3= \mathbb{\mathbf F}(t_n+h/2,\mathbb{\mathbf Y}_n+h \mathbb{\mathbf K}_2/2)\\ \mathbb{\mathbf K}_4= \mathbb{\mathbf F}(t_n+h,\mathbb{\mathbf Y}_n+h \mathbb{\mathbf K}_3)\\ \mathbb{\mathbf Y}_{n+1}=\mathbb{\mathbf Y}_n+h/6(\mathbb{\mathbf K}_1+2\mathbb{\mathbf K}_2+2\mathbb{\mathbf K}_3+\mathbb{\mathbf K}_4+ O(h^5)\\ \end{array} \qquad \mbox{(7)} }[/math]
- The method is initialised with the initial conditions [math]\displaystyle{ \mathbb{\mathbf Y}(t_0) }[/math] and [math]\displaystyle{ \mathbb{\mathbf Y}'(t_0) }[/math]. For the numerical integration of GLONASS satellite orbits, the function [math]\displaystyle{ \mathbb{\mathbf F}(t,\mathbb{\mathbf Y}) }[/math] is given by (7).
- 3. Coordinates transformation back to the PZ-90 reference system:
- The coordinates [math]\displaystyle{ (x(t), y(t), z(t)) }[/math], obtained from the motion equations numerical integration, shall be transformed back to the Earth fixed reference frame PZ-90 with the following equations:
- [math]\displaystyle{ \begin{array}{l} x(t)= x_a(t) cos(\theta_G) + y_a(t) sin (\theta_G)\\ y(t)=- x_a(t) sin(\theta_G) + y_a(t) cos(\theta_G)\\ z(t)= z_a(t) \\ \end{array} \qquad \mbox{(8)} }[/math]
- where [math]\displaystyle{ \theta_G }[/math] is the sidereal time at Greenwich meridian at time [math]\displaystyle{ t }[/math], where [math]\displaystyle{ t }[/math] is in GLONASS time, see equation (4) :
- [math]\displaystyle{ \theta_G= \theta_{G_0} + \omega_E (t - 3~hours) \qquad \mbox{(9)} }[/math]
- [math]\displaystyle{ GLONASS\_time= UTC(SU)-3~hours \qquad \mbox{(10)} }[/math]
- Note that GLONASS satellite coordinates are computed in PZ-90 reference system, instead of WGS-84 where the GPS coordinates have been calculated. To bring the PZ-90 coordinate system in coincidence with WGS-84 the transformation given by equation (11) must be applied (see Reference Frames in GNSS):
- [math]\displaystyle{ \left [ \begin{array}{c} x'\\ y'\\ z'\\ \end{array} \right ] = \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ] + \left [ \begin{array}{ccc} -3\,ppb & -353\,mas & -4\,mas\\ 353\,mas & -3\,ppb & 19\,mas\\ 4\,mas & -19\,mas & -3\,ppb\\ \end{array} \right ] \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ] + \left [ \begin{array}{c} 0.07\,m\\ -0.0\,m\\ -0.77\,m\\ \end{array} \right ] \qquad \mbox{(11)} }[/math]
- The transformation from PZ-90.02 to WGS-84 (actually ITRF2000) is given by [math]\displaystyle{ \Delta x= -0.36\,m }[/math], [math]\displaystyle{ \Delta y= +0.08\, m }[/math], [math]\displaystyle{ \Delta z= +0.18\, m }[/math], with no rotation, i.e., equation (12)[footnotes 2]:
- [math]\displaystyle{ \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ]_{ITRF2000} = \left [ \begin{array}{c} x\\ y\\ z\\ \end{array} \right ]_{PZ-90.02} + \left [ \begin{array}{r} -0.36\,m\\ 0.08 \,m\\ 0.18 \,m\\ \end{array} \right ] \qquad \mbox{(12)} }[/math]
References
- ^ [GLONASS ICD, 1998] GLONASS ICD, 1998. Technical report. v.4.0.
Notes
- ^ Note: Over a small integration intervals, a simple rotation of [math]\displaystyle{ \theta_{G_e} }[/math] angle around Z-axis is enough to perform this transformation. Nutation and precession of the earth and polar motion are a very slow processes and will not introduce significant deviations on such short integration time intervals (see Transformation between Celestial and Terrestrial Frames).
- ^ The PZ-90.02 was implemented in September 20th, 2007 at 18:00. (refer to Reference Frames in GNSS).