If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor

Baseband Processing: Difference between revisions

From Navipedia
Jump to navigation Jump to search
No edit summary
 
(18 intermediate revisions by 6 users not shown)
Line 1: Line 1:
{{Article Infobox2
{{Article Infobox2
|Category=Receivers
|Category=Receivers
|Title={{PAGENAME}}
|Editors=GMV
|Authors=GMV
|Level=Advanced
|Level=Advanced
|YearOfPublication=2011
|YearOfPublication=2011
|Logo=GMV
|Logo=GMV
|Title={{PAGENAME}}
}}
}}
The baseband processing block is responsible for processing the down-converted and digitized GNSS signal in order to provide observables: code pseudo-ranges and carrier phase measurements, as well as navigation data. Additional information, such as Doppler frequency, Carrier-to-Noise ratio, or lock indicators, can also be provided.


 
In most [[Generic Receiver Description|GNSS receivers]]’ architectures, the baseband processing relies on independent channels that track each satellite signal autonomously. Then, the information from each channel is integrated to derive a navigation solution.
The baseband processing block is responsible for processing the down-converted and digitized signal in order to provide GNSS observables: code pseudo-ranges and carrier phase measurements, as well as navigation data. Additional information such as Doppler frequency, Carrier to Noise ratio, lock indicators can also be provided.
In most GNSS receivers’ architectures, the baseband processing relies on independent channels that track each satellite signal autonomously. Then the information from each channel is integrated to derive a navigation solution.


== Block Diagram ==
== Block Diagram ==
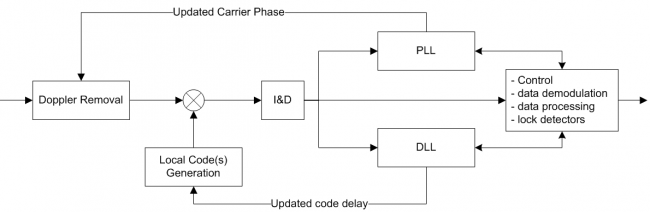
The baseband processing block is usually replicated over several channels. Each channel processes a given signal from a given satellite in order to provide GNSS observables and navigation data. A generic diagram of a single channel within the baseband processing block is depicted in the following figure.


The baseband processing block is usually replicated over several channels. Each channel processes a given signal from a given satellite in order to provide GNSS observables and navigation data.
[[File:bb_block.png|center|thumb|650px|'''''Figure 1:''''' Generic diagram of a single channel in the Baseband Processing block.]]
A generic diagram of a single channel within the Baseband Processing block is depicted in the following figure.


The incoming signal is first stripped of its Doppler frequency (according to the current estimation), and then correlated with one (or more) PRN code replicas generated locally (according to the current estimation of code delay). Then new estimations of the Doppler frequency and code delay are computed based on the assessment of the correlation outputs. Note that for GNSS using FDMA modulation schemes, such as GLONASS, the Doppler removal block represents a shift in the frequency, not only corresponding to the estimated Doppler shift caused by the relative motion between the satellite and the user, but also to the centre frequency of the satellite signal at hand.


[[File:bb_block.png|center|thumb|650px|'''''Figure 1:''''' Generic Diagram of a single channel in the Baseband Procesing block.]]
This process is implemented in an iterative way, usually using PLL and DLL [[Tracking Loops|tracking loops]] to track the incoming signal's phase and code delay, respectively. In parallel, the receiver extracts the navigation data of the incoming signal, and ensures monitoring and control features further described [[Digital Signal Processing|here]].


The incoming signal is firstly stripped of its Doppler frequency (according to its current estimation) and then it is correlated with one (or more) PRN codes generated locally (according to the current estimation of code delay). Then new estimations of the Doppler frequency and code delay are computed based on the assessment of the correlation outputs. Please note that for GNSS using FDMA such as GLONASS, the Doppler removal block represents a shift in the frequency not only corresponding to the estimated Doppler shift caused by the relative motion between the satellite and the user, but also to the center frequency of the satellite at hand.
Please refer to <ref>"GPS Data Processing: Code and Phase Algorithms, Techniques and Recipes", M. Hernandéz, J. Zomoza, J. Sanz, gAGE-NAV, gAGE/ UPC</ref> for additional literature on baseband processing.
This process is implemented in an iterative way, usually using PLL and DLL [[Tracking Loops|tracking loops]] to track the incoming signal phase and code delay respectively.
In parallel, the receiver extracts the navigation data of the incoming signal and ensures monitoring and control features further described [[Digital Signal Processing|here]].


==Principle==
==Principle==
[[File:bb_corr.png|right|thumb|350px|'''''Figure 2:''''' The correlation process: the receiver shifts the code replica (by changing <math>\Delta t\,</math>) until it finds a peak in the correlation output<ref>J. Sanz, J. Zornoza, M. Hernández, “Global Navigation Satellite Systems: Volume I: fundamentals and Algorithms”</ref>.]]
The basic principle of GNSS baseband processing relies on the [[Correlators|correlation process]]. The underlying idea is that GNSS signals convey ranging codes that are built in a way that:
*When the code is correlated with an aligned replica of itself, the correlation output is maximum: high auto-correlation properties.
*When the code is correlated with a non-aligned replica of itself, the correlation output is low.
*When the code is correlated with another code of the same family, the correlation output is low: low cross-correlation properties.
The basic principle is illustrated in Figure 2. The receiver first assigns each channel with a PRN code: for GNSS based on CDMA (such as GPS and Galileo), each satellite transmits a dedicated PRN code, whereas for GNSS based on FDMA (such as GLONASS), the PRN code is the same for all satellites.
At channel level, the incoming signal is correlated with the local replica of this PRN code over time. This local replica is generated in such a way that its code delay and phase characteristics vary, representing a two-dimensional search over code and (Doppler) frequency. Whenever the local replica parameters (code and frequency) match those of the incoming signal, the correlation output will reach a maximum, and the receiver will consider this pair (code and frequency) as the current estimates for these parameters.
Real-life systems are very noisy and dynamic: as a consequence, the auto-correlation peak seems to fluctuate at each time instant. This fact justifies the need for tracking loops (accumulators and filters) to continuously “follow” the incoming signal, since an error of 1 ms in the code delay would lead to an error of around 300 km in the pseudorange measurement.
==Mathematical Model==
At the output of the [[Front End|RF section]], the baseband signal can be written as (neglecting noise):




The basic principle of GNSS baseband processing relies on the [[Correlators|correlation process]]. The underlying idea is that GNSS signals convey ranging codes that are built such as:
<math>s_{BB} (t_k) = \Re\{s(t_k) exp[j\phi (t_k)]\}\,</math>
*When the code is correlated with an aligned replica of itself, the correlation output is maximum: high auto-correlation properties
*When the code is correlated with a non-aligned replica of itself, the correlation output is low
*When the code is correlated with another code of the same family, the correlation output is low: low cross-correlation properties


[[File:bb_corr.png|right|thumb|350px|'''''Figure 2:''''' The Correlation process: the receiver shifts the code replica (by changing <math>\Delta t</math>) until finding a peak in the correlation output<ref>J. Sanz, J. Zornoza, M. Hernández, “Global Navigation Satellite Systems: Volume I: fundamentals and Algorithms”</ref>.]]


with <math>s(t_k) = A_Im_I(t_k)d(t_k)+jA_Qm_Q(t_k)d(t_k)\,</math>


The basic principle is illustrated in Figure 2: the receiver assigns each channel with a PRN code (for GNSS based on CDMA – such as GPS and Galileo - each satellite transmits a dedicated PRN code, whereas for GNSS based on FDMA – such as GLONASS – the PRN code is the same for all satellites).


At channel level, the incoming signal is correlated with the local replica of this PRN code over time. This local replica is generated such that its code delay and phase vary to represent a two-dimensional search over code and (Doppler) frequency. Whenever the local replica code parameters (code and frequency) match those of the incoming signal, the correlation output will reach a maximum and the receiver will consider this pair (code and frequency) as the current estimates for these parameters.
where:


*<math>A\,</math> is the signal amplitude.
*<math>m(t_k)\,</math> = ±1, and it includes the PRN code and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, <math>m_I(t_k)\,</math> and <math>m_Q(t_k)\,</math> are the C/A code and the P code respectively.
*<math>d(t_k)\,</math> is the navigation data. Note that if no data is transmitted (e.g. pilot channels), this term is always 1.
*<math>I\,</math> and <math>Q\,</math> refer to the In-phase and the Quadrature components, respectively.
*<math>\phi (t_k)\,</math> accounts for the phase information, including Doppler frequency, receiver clock instabilities and initial signal phase.


Real-life systems are very noisy and dynamic: as a consequence, the auto-correlation peak seems to fluctuate at each time instant, hence the need for tracking loops (accumulators and filters) to continuously “follow” the incoming signal, as an error of 1 ms in the code delay would lead to an error of around 300 km in the pseudorange measurement.


==Mathematical Model==
The Doppler removal block rotates the complex baseband signal by the current estimation of the carrier phase:


At the output of the [[Front End|RF section]], the baseband signal was written as (neglecting noise):


<math>s_{BB} (t_k) = \Re\{s(t_k) exp[j\phi (t_k)]\}\,</math>
<math>s_{out} (t_k) = s(t_k) exp[j\phi_e (t_k)]\}\,</math>


with <math>s(t_k) = A_Im_I(t_k)d(t_k)-jA_Qm_Q(t_k)d(t_k)\,</math>


where:
where:
*<math>A</math> is the signal amplitude
*<math>m(t_k)</math> = ±1 and it includes the PRN code, navigation data (if applicable) and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, <math>m_I(t_k)</math> and <math>m_Q(t_k)</math> are the C/A code and the P code respectively
*<math>d(t_k)</math> is the navigation data. Please note that in case no data is transmitted (e.g. pilot channels) this term is replaced by 1
* I and Q refer to the In-phase and the Quadrature components respectively
*<math>\phi (t_k)</math> accounts for the phase including Doppler frequency, receiver clock instabilities and initial signal phase.


The Doppler removal block rotates the complex baseband signal by the current estimation of the carrier phase:
*the phase error is given by <math>\phi_e (t_k)=\hat{\phi}(t_k)-\phi(t_k)\,</math>
*<math>\hat{\phi}(t_k)\,</math> is the phase estimated at the receiver.
*<math>\phi(t_k)\,</math> is the phase of the incoming signal.
 
 
The correlation between the incoming signal and the local (PRN) code replica corresponds to the ''correlators'' and ''accumulators'' blocks, and can be written as:


<math>s_{out} (t_k) = s_{BB}(t_k) exp[j\phi_e (t_k)]\}\,</math>


where
<math>Corr_{out}(\hat{\tau}) = \sum_T s_{out}^{*} (t_k) m(t_k-\hat{\tau})\,</math>
*the phase error is given by <math>\phi_e (t_k)=\hat{\phi}(t_k)-\phi(t_k)</math>
*<math>\hat{\phi}(t_k)</math> is the phase estimated at the receiver
*<math>\phi(t_k)</math> is the phase of the incoming signal


The correlation between the incoming signal and the local (PRN) code replica corresponds to the “correlators” and “accumulators” blocks, and can be written as:


<math>Corr_{out}(\hat{\tau}) = \sum_T s_{out}^{*} (t_k) m(t_k-\hat{\tau})</math>
where:
 
*<math>T\,</math> is the integration time, i.e. the accumulation interval.
*<math>\hat{\tau}\,</math> is the code delay estimated at the receiver.


where
* T is the integration time, i.e. the accumulation interval
*<math>\hat{\tau} </math> is the code delay estimated at the receiver


As an example, the correlation output for a receiver tracking GPS L1 C/A code would be:
As an example, the correlation output for a receiver tracking GPS L1 C/A code would be:


<math>Corr_{out}(\hat{\tau}) = \sum_T (A_Id(t_k)c_I(t_k) + jA_Qd(t_k)c_Q(t_k))  exp[-j\phi_e(t_k)]  c_I(t_k - \hat{\tau})</math>


where
<math>Corr_{out}(\hat{\tau}) = \sum_T (A_Id(t_k)c_I(t_k) + jA_Qd(t_k)c_Q(t_k))  exp[-j\phi_e(t_k)]  c_I(t_k - \hat{\tau})\,</math>
*<math>c_I</math> would stand for C/A code
 
*<math>c_Q</math> would stand for the P code
 
*<math>c_I(t_k - \hat{\tau})</math> is the local replica generated at the receiver
where:
 
*<math>c_I\,</math> would stand for C/A code.
*<math>c_Q\,</math> would stand for the P code.
*<math>c_I(t_k - \hat{\tau})\,</math> is the local replica generated at the receiver.
 


Considering that the cross-correlation between C/A code and P code can be neglected, the expression can be simplified to:
Considering that the cross-correlation between C/A code and P code can be neglected, the expression can be simplified to:


<math>Corr_{out}(\hat{\tau}) = \sum_T A_Id(t_k)c_I(t_k)  exp[-j\phi_e(t_k)]  c_I(t_k - \hat{\tau})</math>


Hence the output of the correlation and accumulation blocks can be written in its in-phase (I) and quadrature (Q) components as:
<math>Corr_{out}(\hat{\tau}) = \sum_T A_Id(t_k)c_I(t_k)  exp[-j\phi_e(t_k)]  c_I(t_k - \hat{\tau})\,</math>
 
 
Hence the output of the correlation and accumulation blocks can be written in its in-phase (<math>I\,</math>) and quadrature (<math>Q\,</math>) components as:


<math>I_P = A_I d_I R_{c_I} (\tau_e) cos(\phi_e) </math>


<math>Q_P = -A_Id_IR_{c_I}(\tau_e)sin(\phi_e) </math>
<math>I_P = A_I d_I R_{c_I} (\tau_e) cos(\phi_e)\,</math>


<math>Q_P = -A_Id_IR_{c_I}(\tau_e)sin(\phi_e)\,</math>


where
*<math>R_{c_I}</math> is the auto-correlation of the <math>c_I</math> code
*<math>P</math> stands for the Prompt replica, i.e. the replica generated at the receiver which is aligned with the incoming signal.
*<math>\tau_e</math> is the error of the code delay estimated at the receiver
*<math>\phi_e</math> is the error of the carrier phase estimated at the receiver


The correlation outputs are then fed to the [[Tracking Loops|tracking loops]].
where:


Further information about GNSS receiver correlators can be found [[Correlators|here]].
*<math>R_{c_I}\,</math> is the auto-correlation of the <math>c_I\,</math> code.
*<math>P\,</math> stands for the Prompt replica, i.e. the replica generated at the receiver which is aligned with the incoming signal.
*<math>\tau_e\,</math> is the error of the code delay estimated at the receiver.
*<math>\phi_e\,</math> is the error of the carrier phase estimated at the receiver.


The correlation outputs are then fed to the [[Tracking Loops|tracking loops]]. Further information about GNSS receiver correlators can be found [[Correlators|here]].


== Signal Detection ==
== Signal Detection ==
In the previous sections it's assumed that a current estimate of the parameter pair {code delay, Doppler frequency} was already available, and therefore the receiver would generate the local PRN code replica using those parameter estimates. However, when a channel is first set up, these estimates are usually not available, and therefore each channel will launch a ''cold'' search for the signal. The channel is said to be in '''Acquisition''' mode when searching for signals, and then transits to '''Tracking''' mode once the signal is found. For further information on receiver operations, see [[Receiver Operations|here]].


In the last sections it has been considered that a current estimate of the pair of parameters [code delay, Doppler frequency] was already available and therefore the receiver would generate the local PRN code replica using those parameters.
When in acquisition mode, each channel is looking for all possible pairs of {code delay, Doppler frequency}, by generating a set of possible local replicas, and correlating each of them with the incoming signal. The power of the correlation output is somehow a measure of how good (or how close to the real signal) the estimates of the code delay and carrier phase are. Nevertheless, the correlation outputs described up to now are all based on the assumption that the signals are not subject to noise: in fact, the signal is actually so noisy that a single shot decision process on the correlation results has a very low probability of detecting the presence of a signal.
When a channel is first set up, however, these estimates are usually not available and therefore each channel will launch a cold search for the signal. The channel is said to be in Acquisition mode, and then transits to Tracking mode once the signal has been found, further information [[Receiver Operations|here]].


When in acquisition mode, each channel is looking for all possible pairs of [code delay, Doppler frequency] by generating all possible local replicas and correlating them with the incoming signal. The power of the correlation output is somehow a measure of how good the estimates of the code delay and the carrier phase are.
The auto-correlation outputs seen until now are all based on the assumption that the signals are not subject to noise. In general, the signal is actually so noisy that a single shot decision process has very low probability of detecting it.
The presence of a signal is assessed using the following decision statistic:
The presence of a signal is assessed using the following decision statistic:


<math>z= \sum_{k=1}^M |Y(k)|^2</math>


where
<math>z= \sum_{k=1}^M |Y(k)|^2\,</math>
*M is the number of non-coherent integrations
 
*Y is the output of teh correlation of the incoming signal with the local replica ^(complex) over the coherent integration time, T
 
*k refers to the kth coherent integration interval
where:
 
*<math>M\,</math> is the number of non-coherent integrations.
*<math>Y\,</math> is the output of the correlation of the incoming signal with the local replica (complex) over the coherent integration time <math>T\,</math>.
*<math>k\,</math> refers to the <math>k\,</math>''th'' coherent integration interval.




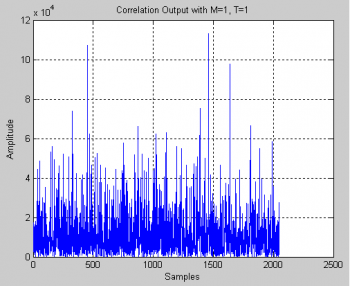
[[File:int_1_1.png|right|thumb|350px|'''''Figure 3:'''''Example of the correlation output for different code delays using 1 coherent and 1 non-coherent integration times.]]
[[File:int_1_1.png|right|thumb|350px|'''''Figure 3:'''''Example of the correlation output for different code delays using 1 coherent and 1 non-coherent integration times.]]
The statistic <math>z\,</math> is then compared to a detection threshold, to assess whether the signal is present or not. This detection threshold is defined according to a target probability of false alarm.
In this process, the correlation outputs are actually integrated over time before further processing: this is gathered in the block ''I&D'', standing for ''Integrate and Dump'', in Figure 1. Two types of integration can be considered:


*'''Coherent integrations''': this technique consists in using longer integration times (multiples of the code length) before dumping the correlation output. Although this technique reduces noise, its performance is limited by the bit boundaries that carry the navigation message: in fact, if the integration time is such that it straddles the bit boundaries, then the correlation output is bound to lose overall power.


The statistic z is then compared to a detection threshold to assess whether the signal is present or not. The detection threshold is defined according to a target probability of false alarm.
*'''Non-coherent integrations''': this technique consists in adding the results of ''single shot'' correlations together, before entering the decision process.
Therefore the correlation outputs are actually integrated over time before further processing, this is comprised in the block “I&D”, standing for Integrate and Dump in figure 1.  


Two types of integration can be considered:
Due to squaring losses, the first technique is more effective that the latter, although limited by the navigation bit boundaries. As an example, Figure 3 represents the correlation outputs for all possible code delays in one single Doppler frequency (which we know beforehand to be the correct one). In this case, one coherent and one non-coherent integration were considered.
*Coherent integrations: this technique consists in using longer data (multiples of the code length) before dumping the correlation output. Although this technique reduces noise, it is limited by the bit boundaries that carry the navigation message. In fact, if the integration time is such that it straddles the bit boundaries, then the correlation output is bound to lose power overall.
*Non-coherent integrations: This technique consists in adding “single shot” correlations together before entering the decision process
Due to the squaring losses, the first technique is more effective that the latter, although limited by the navigation bit boundaries.
As an example, figure 3 represents the correlation outputs for all possible code delays in one single Doppler frequency (which we know beforehand to be the correct one). In this case, one 1 coherent and 1 non-coherent integration was considered.


Due to the noisy conditions, it is clear that the correlation peak is not visible from these results.
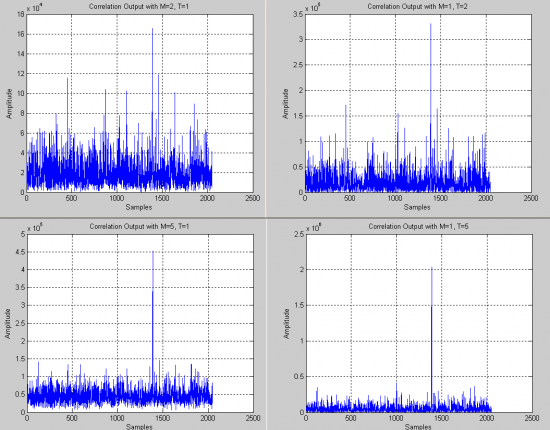
Because of the noisy conditions of GNSS signals, it is clear that the correlation peak is not visible from these results. To illustrate further, Figure 4 shows the correlation results for the same signal with different coherent (''T'') and non-coherent (''M'') integration times. The power increase becomes clear as ''M'' and ''T'' increase, hence showing clearly the correlation peak. The abscise value can be processed to yield a first estimate of the code delay.
Figure 4 shows the correlations for the same signal with different coherent (T) and non-coherent (M) integration values. The power increase becomes clear as M and T increase, hence showing clearly the correlation peak. The abscise value can be process to yield a first estimate on the code delay.


[[File:integrations.png|center|thumb|550px|'''''Figure 4:'''''Example of the correlation output for different code delays using different coherent and non-coherent integration times.]]
[[File:integrations.png|center|thumb|550px|'''''Figure 4:'''''Example of the correlation output for different code delays using different coherent and non-coherent integration times.]]


On one hand, the examples shown in Figure 4 illustrates how coherent integrations bring more benefits (higher power and lower noise floor) when compared to non-coherent integrations, which need to cope with squaring losses. On the other hand, non-coherent integrations are safer to implement (before bit synchronization), since they do not need to take into account the straddling navigation bit boundaries.


On one hand, the examples shown in this figure show how coherent integrations bring more benefits (higher power and lower noise floor) when compared to non-coherent integrations that need to cope with squaring losses. One the other hand, non-coherent integrations are safer to implement (before bit synchronization) since they do not need to care about straddling navigation bit boundaries.
Finally, the dimensioning of these techniques has to consider the expected noise conditions, probability of false alarm, probability of detection and mean acquisition time. In fact, the longer the integrations the higher probability of detection (the lower the probability of false alarm) but the slower the potential acquisition time is, since the receiver will dwell longer in each search bin, defined by the pair [code delay, Doppler frequency].
Finally, the dimensioning of these techniques has to consider the expected noise conditions, probability of false alarm, probability of detection and mean acquisition time. In fact, the longer the integrations the higher probability of detection (the lower the probability of false alarm) but the slower the potential acquisition time is, since the receiver will dwell longer in each search bin, defined by the pair [code delay, Doppler frequency].


The concepts of coherent and non-coherent integrations are also used when the receiver is in tracking mode in order to reduce the noise levels and increase accuracy, see [[Tracking Loops|tracking loops]]. The advantage is that, after bit synchronization, the receiver may increase the integration time up to the bit duration (20ms for GPS L1 C/A). Modernized GNSS such as Galileo already have so-called pilot channels that do not convey any navigation data and therefore can be used to further extend (coherent) integration times.
The concepts of coherent and non-coherent integrations are also used when the receiver is in tracking mode, in order to reduce the noise levels and increase accuracy (see [[Tracking Loops|tracking loops]] for details). The advantage is that, after bit synchronization, the receiver may increase the integration time up to the bit duration (e.g. 20 ms for GPS L1 C/A<ref>[GPS ICD 200, 2006] IS-GPS-200 Revision D, IRN-200D-001:NAVSTAR GLOBAL POSITIONING SYSTEM Navstar GPS Space Segment/Navigation User Interface, dated 7 March 2006.
Long integration times are also used to track weak signals in harsh environments (such as indoors); but they are limited both by the data bit and by the accuracy of the clock/Doppler frequency estimation<ref>DINGPOS: A Hybrid Indoor Navigation Platform for GPS and GALILEO, J. A. López-Salcedo (UAB) , Y. Capelle (TAS-F), M. Toledo (GMV), G. Seco (UAB), J. López Vicario (UAB), D. Kubrak (TAS-F), M. Monnerat (TAS-F), A. Mark (GMV), D. Jiménez (ESA), ION GNSS 2008</ref>.
</ref>). Modernized GNSS such as Galileo already have so-called pilot channels that do not convey any navigation data, and therefore can be used to further extend (coherent) integration times.


Long integration times are also used to track weak signals in harsh environments (such as indoors), but they are limited both by the data bit and by the accuracy of the clock/Doppler frequency estimation<ref>DINGPOS: A Hybrid Indoor Navigation Platform for GPS and GALILEO, J. A. López-Salcedo (UAB) , Y. Capelle (TAS-F), M. Toledo (GMV), G. Seco (UAB), J. López Vicario (UAB), D. Kubrak (TAS-F), M. Monnerat (TAS-F), A. Mark (GMV), D. Jiménez (ESA), ION GNSS 2008.</ref>.


==Platforms==
==Platforms==
 
Most receivers implement the baseband processing algorithms in dedicated ASICs, DSPs or even FPGAs, as discussed [[Receiver Types|here]]. The baseband processing block, however, may also be implemented in software, following a Software Defined Radio (SDR)<ref>[[Wikipedia:Software GNSS Receiver|Software GNSS Receiver in Wikipedia]]</ref> philosophy. Although the software implementations provide a higher degree of flexibility, upgradeability and expandability, they still raise concerns regarding processing load and CPU power consumption in current commercial platforms<ref>http://www.gpsworld.com</ref>.
Platform
Most receivers implement the baseband processing algorithms in dedicated ASICs, DSPs or even FPGAs, [link to Receiver Types]. The baseband processing block, however, may also be implemented in software, following a Software Defined Radio (SDR) philosophy<ref>http://en.wikipedia.org/wiki/Software_GNSS_Receiver</ref>.
Although the software implementations provide a higher degree of flexibility, upgradeability and expandability, they still raise concerns regarding processing load and CPU power consumption in current commercial platforms<ref>http://www.gpsworld.com/gps/the-software-gnss-receiver-936</ref>.
 


==Related articles==
==Related articles==
Line 159: Line 167:
*[[Antennas]]
*[[Antennas]]
*[[Receiver Characteristics]]
*[[Receiver Characteristics]]
*[[Baseband Processing]]
*[[Digital Signal Processing]]


==References==
==References==

Latest revision as of 08:57, 24 January 2024


ReceiversReceivers
Title Baseband Processing
Edited by GMV
Level Advanced
Year of Publication 2011
Logo GMV.png

The baseband processing block is responsible for processing the down-converted and digitized GNSS signal in order to provide observables: code pseudo-ranges and carrier phase measurements, as well as navigation data. Additional information, such as Doppler frequency, Carrier-to-Noise ratio, or lock indicators, can also be provided.

In most GNSS receivers’ architectures, the baseband processing relies on independent channels that track each satellite signal autonomously. Then, the information from each channel is integrated to derive a navigation solution.

Block Diagram

The baseband processing block is usually replicated over several channels. Each channel processes a given signal from a given satellite in order to provide GNSS observables and navigation data. A generic diagram of a single channel within the baseband processing block is depicted in the following figure.

Figure 1: Generic diagram of a single channel in the Baseband Processing block.

The incoming signal is first stripped of its Doppler frequency (according to the current estimation), and then correlated with one (or more) PRN code replicas generated locally (according to the current estimation of code delay). Then new estimations of the Doppler frequency and code delay are computed based on the assessment of the correlation outputs. Note that for GNSS using FDMA modulation schemes, such as GLONASS, the Doppler removal block represents a shift in the frequency, not only corresponding to the estimated Doppler shift caused by the relative motion between the satellite and the user, but also to the centre frequency of the satellite signal at hand.

This process is implemented in an iterative way, usually using PLL and DLL tracking loops to track the incoming signal's phase and code delay, respectively. In parallel, the receiver extracts the navigation data of the incoming signal, and ensures monitoring and control features further described here.

Please refer to [1] for additional literature on baseband processing.

Principle

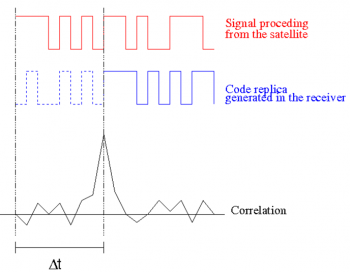
Figure 2: The correlation process: the receiver shifts the code replica (by changing [math]\displaystyle{ \Delta t\, }[/math]) until it finds a peak in the correlation output[2].

The basic principle of GNSS baseband processing relies on the correlation process. The underlying idea is that GNSS signals convey ranging codes that are built in a way that:

  • When the code is correlated with an aligned replica of itself, the correlation output is maximum: high auto-correlation properties.
  • When the code is correlated with a non-aligned replica of itself, the correlation output is low.
  • When the code is correlated with another code of the same family, the correlation output is low: low cross-correlation properties.

The basic principle is illustrated in Figure 2. The receiver first assigns each channel with a PRN code: for GNSS based on CDMA (such as GPS and Galileo), each satellite transmits a dedicated PRN code, whereas for GNSS based on FDMA (such as GLONASS), the PRN code is the same for all satellites.

At channel level, the incoming signal is correlated with the local replica of this PRN code over time. This local replica is generated in such a way that its code delay and phase characteristics vary, representing a two-dimensional search over code and (Doppler) frequency. Whenever the local replica parameters (code and frequency) match those of the incoming signal, the correlation output will reach a maximum, and the receiver will consider this pair (code and frequency) as the current estimates for these parameters.

Real-life systems are very noisy and dynamic: as a consequence, the auto-correlation peak seems to fluctuate at each time instant. This fact justifies the need for tracking loops (accumulators and filters) to continuously “follow” the incoming signal, since an error of 1 ms in the code delay would lead to an error of around 300 km in the pseudorange measurement.

Mathematical Model

At the output of the RF section, the baseband signal can be written as (neglecting noise):


[math]\displaystyle{ s_{BB} (t_k) = \Re\{s(t_k) exp[j\phi (t_k)]\}\, }[/math]


with [math]\displaystyle{ s(t_k) = A_Im_I(t_k)d(t_k)+jA_Qm_Q(t_k)d(t_k)\, }[/math]


where:

  • [math]\displaystyle{ A\, }[/math] is the signal amplitude.
  • [math]\displaystyle{ m(t_k)\, }[/math] = ±1, and it includes the PRN code and modulation information (e.g. subcarrier code for BOC modulations). For the case of GPS L1, [math]\displaystyle{ m_I(t_k)\, }[/math] and [math]\displaystyle{ m_Q(t_k)\, }[/math] are the C/A code and the P code respectively.
  • [math]\displaystyle{ d(t_k)\, }[/math] is the navigation data. Note that if no data is transmitted (e.g. pilot channels), this term is always 1.
  • [math]\displaystyle{ I\, }[/math] and [math]\displaystyle{ Q\, }[/math] refer to the In-phase and the Quadrature components, respectively.
  • [math]\displaystyle{ \phi (t_k)\, }[/math] accounts for the phase information, including Doppler frequency, receiver clock instabilities and initial signal phase.


The Doppler removal block rotates the complex baseband signal by the current estimation of the carrier phase:


[math]\displaystyle{ s_{out} (t_k) = s(t_k) exp[j\phi_e (t_k)]\}\, }[/math]


where:

  • the phase error is given by [math]\displaystyle{ \phi_e (t_k)=\hat{\phi}(t_k)-\phi(t_k)\, }[/math]
  • [math]\displaystyle{ \hat{\phi}(t_k)\, }[/math] is the phase estimated at the receiver.
  • [math]\displaystyle{ \phi(t_k)\, }[/math] is the phase of the incoming signal.


The correlation between the incoming signal and the local (PRN) code replica corresponds to the correlators and accumulators blocks, and can be written as:


[math]\displaystyle{ Corr_{out}(\hat{\tau}) = \sum_T s_{out}^{*} (t_k) m(t_k-\hat{\tau})\, }[/math]


where:

  • [math]\displaystyle{ T\, }[/math] is the integration time, i.e. the accumulation interval.
  • [math]\displaystyle{ \hat{\tau}\, }[/math] is the code delay estimated at the receiver.


As an example, the correlation output for a receiver tracking GPS L1 C/A code would be:


[math]\displaystyle{ Corr_{out}(\hat{\tau}) = \sum_T (A_Id(t_k)c_I(t_k) + jA_Qd(t_k)c_Q(t_k)) exp[-j\phi_e(t_k)] c_I(t_k - \hat{\tau})\, }[/math]


where:

  • [math]\displaystyle{ c_I\, }[/math] would stand for C/A code.
  • [math]\displaystyle{ c_Q\, }[/math] would stand for the P code.
  • [math]\displaystyle{ c_I(t_k - \hat{\tau})\, }[/math] is the local replica generated at the receiver.


Considering that the cross-correlation between C/A code and P code can be neglected, the expression can be simplified to:


[math]\displaystyle{ Corr_{out}(\hat{\tau}) = \sum_T A_Id(t_k)c_I(t_k) exp[-j\phi_e(t_k)] c_I(t_k - \hat{\tau})\, }[/math]


Hence the output of the correlation and accumulation blocks can be written in its in-phase ([math]\displaystyle{ I\, }[/math]) and quadrature ([math]\displaystyle{ Q\, }[/math]) components as:


[math]\displaystyle{ I_P = A_I d_I R_{c_I} (\tau_e) cos(\phi_e)\, }[/math]

[math]\displaystyle{ Q_P = -A_Id_IR_{c_I}(\tau_e)sin(\phi_e)\, }[/math]


where:

  • [math]\displaystyle{ R_{c_I}\, }[/math] is the auto-correlation of the [math]\displaystyle{ c_I\, }[/math] code.
  • [math]\displaystyle{ P\, }[/math] stands for the Prompt replica, i.e. the replica generated at the receiver which is aligned with the incoming signal.
  • [math]\displaystyle{ \tau_e\, }[/math] is the error of the code delay estimated at the receiver.
  • [math]\displaystyle{ \phi_e\, }[/math] is the error of the carrier phase estimated at the receiver.


The correlation outputs are then fed to the tracking loops. Further information about GNSS receiver correlators can be found here.

Signal Detection

In the previous sections it's assumed that a current estimate of the parameter pair {code delay, Doppler frequency} was already available, and therefore the receiver would generate the local PRN code replica using those parameter estimates. However, when a channel is first set up, these estimates are usually not available, and therefore each channel will launch a cold search for the signal. The channel is said to be in Acquisition mode when searching for signals, and then transits to Tracking mode once the signal is found. For further information on receiver operations, see here.

When in acquisition mode, each channel is looking for all possible pairs of {code delay, Doppler frequency}, by generating a set of possible local replicas, and correlating each of them with the incoming signal. The power of the correlation output is somehow a measure of how good (or how close to the real signal) the estimates of the code delay and carrier phase are. Nevertheless, the correlation outputs described up to now are all based on the assumption that the signals are not subject to noise: in fact, the signal is actually so noisy that a single shot decision process on the correlation results has a very low probability of detecting the presence of a signal.

The presence of a signal is assessed using the following decision statistic:


[math]\displaystyle{ z= \sum_{k=1}^M |Y(k)|^2\, }[/math]


where:

  • [math]\displaystyle{ M\, }[/math] is the number of non-coherent integrations.
  • [math]\displaystyle{ Y\, }[/math] is the output of the correlation of the incoming signal with the local replica (complex) over the coherent integration time [math]\displaystyle{ T\, }[/math].
  • [math]\displaystyle{ k\, }[/math] refers to the [math]\displaystyle{ k\, }[/math]th coherent integration interval.


Figure 3:Example of the correlation output for different code delays using 1 coherent and 1 non-coherent integration times.

The statistic [math]\displaystyle{ z\, }[/math] is then compared to a detection threshold, to assess whether the signal is present or not. This detection threshold is defined according to a target probability of false alarm.

In this process, the correlation outputs are actually integrated over time before further processing: this is gathered in the block I&D, standing for Integrate and Dump, in Figure 1. Two types of integration can be considered:

  • Coherent integrations: this technique consists in using longer integration times (multiples of the code length) before dumping the correlation output. Although this technique reduces noise, its performance is limited by the bit boundaries that carry the navigation message: in fact, if the integration time is such that it straddles the bit boundaries, then the correlation output is bound to lose overall power.
  • Non-coherent integrations: this technique consists in adding the results of single shot correlations together, before entering the decision process.

Due to squaring losses, the first technique is more effective that the latter, although limited by the navigation bit boundaries. As an example, Figure 3 represents the correlation outputs for all possible code delays in one single Doppler frequency (which we know beforehand to be the correct one). In this case, one coherent and one non-coherent integration were considered.

Because of the noisy conditions of GNSS signals, it is clear that the correlation peak is not visible from these results. To illustrate further, Figure 4 shows the correlation results for the same signal with different coherent (T) and non-coherent (M) integration times. The power increase becomes clear as M and T increase, hence showing clearly the correlation peak. The abscise value can be processed to yield a first estimate of the code delay.

Figure 4:Example of the correlation output for different code delays using different coherent and non-coherent integration times.

On one hand, the examples shown in Figure 4 illustrates how coherent integrations bring more benefits (higher power and lower noise floor) when compared to non-coherent integrations, which need to cope with squaring losses. On the other hand, non-coherent integrations are safer to implement (before bit synchronization), since they do not need to take into account the straddling navigation bit boundaries.

Finally, the dimensioning of these techniques has to consider the expected noise conditions, probability of false alarm, probability of detection and mean acquisition time. In fact, the longer the integrations the higher probability of detection (the lower the probability of false alarm) but the slower the potential acquisition time is, since the receiver will dwell longer in each search bin, defined by the pair [code delay, Doppler frequency].

The concepts of coherent and non-coherent integrations are also used when the receiver is in tracking mode, in order to reduce the noise levels and increase accuracy (see tracking loops for details). The advantage is that, after bit synchronization, the receiver may increase the integration time up to the bit duration (e.g. 20 ms for GPS L1 C/A[3]). Modernized GNSS such as Galileo already have so-called pilot channels that do not convey any navigation data, and therefore can be used to further extend (coherent) integration times.

Long integration times are also used to track weak signals in harsh environments (such as indoors), but they are limited both by the data bit and by the accuracy of the clock/Doppler frequency estimation[4].

Platforms

Most receivers implement the baseband processing algorithms in dedicated ASICs, DSPs or even FPGAs, as discussed here. The baseband processing block, however, may also be implemented in software, following a Software Defined Radio (SDR)[5] philosophy. Although the software implementations provide a higher degree of flexibility, upgradeability and expandability, they still raise concerns regarding processing load and CPU power consumption in current commercial platforms[6].

Related articles

References

  1. ^ "GPS Data Processing: Code and Phase Algorithms, Techniques and Recipes", M. Hernandéz, J. Zomoza, J. Sanz, gAGE-NAV, gAGE/ UPC
  2. ^ J. Sanz, J. Zornoza, M. Hernández, “Global Navigation Satellite Systems: Volume I: fundamentals and Algorithms”
  3. ^ [GPS ICD 200, 2006] IS-GPS-200 Revision D, IRN-200D-001:NAVSTAR GLOBAL POSITIONING SYSTEM Navstar GPS Space Segment/Navigation User Interface, dated 7 March 2006.
  4. ^ DINGPOS: A Hybrid Indoor Navigation Platform for GPS and GALILEO, J. A. López-Salcedo (UAB) , Y. Capelle (TAS-F), M. Toledo (GMV), G. Seco (UAB), J. López Vicario (UAB), D. Kubrak (TAS-F), M. Monnerat (TAS-F), A. Mark (GMV), D. Jiménez (ESA), ION GNSS 2008.
  5. ^ Software GNSS Receiver in Wikipedia
  6. ^ http://www.gpsworld.com
Retrieved from "https://gssc.esa.int/navipedia/index.php?title=Baseband_Processing&oldid=16093"