If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Mapping of Niell: Difference between revisions
Carlos.Lopez (talk | contribs) (Created page with "{{Article Infobox2 |Category=Fundamentals |Title={{PAGENAME}} |Authors=J. Sanz Subirana, JM. Juan Zornoza and M. Hernandez-Pajares, University of Catalunia, Spain. |Level=Basic |...") |
Carlos.Lopez (talk | contribs) No edit summary |
||
| (9 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Article Infobox2 | {{Article Infobox2 | ||
|Category=Fundamentals | |Category=Fundamentals | ||
|Authors=J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. | |||
|Level=Advanced | |||
|YearOfPublication=2011 | |||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
A mapping function that does not require surface meteorology measurements, but provides comparable accuracy and precision to others that requires such data is presented in [Niell, 1996]<ref> [Niell, 1996] Niell, A., 1996. Global mapping functions for the atmosphere delay at radio wavelengths. Journal of Geophysical Research. 101, pp. 3227-3246.</ref>. This mapping only | A mapping function that does not require surface meteorology measurements, but provides comparable accuracy and precision to others that requires such data is presented in [Niell, 1996]<ref> [Niell, 1996] Niell, A., 1996. Global mapping functions for the atmosphere delay at radio wavelengths. Journal of Geophysical Research. 101, pp. 3227-3246.</ref>. This mapping only uses the receiver geographic location and measurement time as inputs. | ||
The Niell's mapping involves two different obliquity factors, for the dry and wet components, which are computed from the equations (1) to (4), where <math>(E)</math> is the elevation of ray and <math>(H)</math> is the receiver height, in kilometres: | The Niell's mapping involves two different obliquity factors, for the dry and wet components, which are computed from the equations (1) to (4), where <math>(E)</math> is the elevation of ray and <math>(H)</math> is the receiver height, in kilometres: | ||
| Line 27: | Line 28: | ||
where, <math>m(E,a,b,c)</math> is the [Marini, 1972]<ref> [Marini, 1972] Marini, J., 1972. Correction of Satellite tracking data for an arbitrary Tropospheric Pro_le. Radio Science. 7(2), pp. 223-231.</ref> mapping normalised to unity at zenith: | ::where, <math>m(E,a,b,c)</math> is the [Marini, 1972]<ref> [Marini, 1972] Marini, J., 1972. Correction of Satellite tracking data for an arbitrary Tropospheric Pro_le. Radio Science. 7(2), pp. 223-231.</ref> mapping normalised to unity at zenith: | ||
::<math> | ::<math> | ||
| Line 33: | Line 35: | ||
* The Hydrostatic parameters <math>a_d</math>, <math>b_d</math>, <math>c_d</math> are time <math>(t)</math> and latitude (<math>\ | |||
* The Hydrostatic parameters <math>a_d</math>, <math>b_d</math>, <math>c_d</math> are time <math>(t)</math> and latitude (<math>\Phi)</math> dependent parameters given by: | |||
::<math> | ::<math> | ||
| Line 39: | Line 42: | ||
where, <math>t</math> is the time from January <math>0.0</math>, in days, and <math>T_0</math> is taken as DoY <math>28</math> (i.e., <math>T_0=28</math>). The parameters <math>\xi_{_{avg}}(\phi_i)</math> and <math>\xi_{_{amp}}(\phi_i)</math> are linearly interpolated from table 1 between the nearest <math>\xi(\ | where, <math>t</math> is the time from January <math>0.0</math>, in days, and <math>T_0</math> is taken as DoY <math>28</math> (i.e., <math>T_0=28</math>). The parameters <math>\xi_{_{avg}}(\phi_i)</math> and <math>\xi_{_{amp}}(\phi_i)</math> are linearly interpolated from table 1 between the nearest <math>\xi(\Phi_i)</math>. The <math>a_{ht}</math>, <math>b_{ht}</math>, <math>c_{ht}</math> are taken directly from the same table 1. | ||
*The wet parameters <math>a_w</math>, <math>b_w</math>, <math>c_w</math> are latitude dependent and are linearly interpolated from table 2 between the nearest <math>\xi(\ | *The wet parameters <math>a_w</math>, <math>b_w</math>, <math>c_w</math> are latitude dependent and are linearly interpolated from table 2 between the nearest <math>\xi(\Phi_i)</math>. | ||
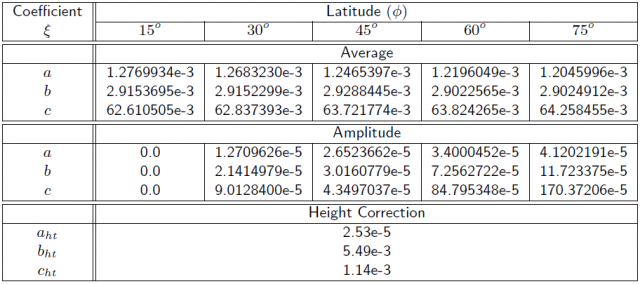
::[[File:Niell_Mapping_Table_1.png|none|thumb| | ::[[File:Niell_Mapping_Table_1.png|none|thumb|640px|'''''Table 1:''''' Coefficients of the hydrostatic mapping function.]] | ||
::[[File:Niell_Mapping_Table_2.png|none|thumb| | ::[[File:Niell_Mapping_Table_2.png|none|thumb|640px|'''''Table 2:''''' Coefficients of the wet mapping function.]] | ||
| Line 56: | Line 60: | ||
[[Category:Fundamentals]] | [[Category:Fundamentals]] | ||
[[Category:GNSS Measurements Modelling]] | |||
Latest revision as of 11:35, 23 February 2012
| Fundamentals | |
|---|---|
| Title | Mapping of Niell |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
A mapping function that does not require surface meteorology measurements, but provides comparable accuracy and precision to others that requires such data is presented in [Niell, 1996][1]. This mapping only uses the receiver geographic location and measurement time as inputs.
The Niell's mapping involves two different obliquity factors, for the dry and wet components, which are computed from the equations (1) to (4), where [math]\displaystyle{ (E) }[/math] is the elevation of ray and [math]\displaystyle{ (H) }[/math] is the receiver height, in kilometres:
Hydrostatic mapping function:
- [math]\displaystyle{ \begin{array}{l} M_{dry}(E,H)= m(E,a_d,b_d,c_d)+ \Delta m(E,H)\\ \qquad\mbox{with}\\ \Delta m(E,H)= \left[ \frac{1}{sin E} - m(E,a_{ht},b_{ht},c_{ht}) \right ] \cdot H \end{array} \qquad\mbox{(1)} }[/math]
Wet Mapping Function:
- [math]\displaystyle{ M_{wet}(E)= m(E,a_w,b_w,c_w) \qquad\mbox{(2)} }[/math]
- where, [math]\displaystyle{ m(E,a,b,c) }[/math] is the [Marini, 1972][2] mapping normalised to unity at zenith:
- [math]\displaystyle{ m(E,a,b,c)= \frac{1+\frac{a}{1+\frac{b}{1+c}}}{\sin E+\frac{a}{\sin E+\frac{b}{\sin E+c}}} \qquad\mbox{(3)} }[/math]
- The Hydrostatic parameters [math]\displaystyle{ a_d }[/math], [math]\displaystyle{ b_d }[/math], [math]\displaystyle{ c_d }[/math] are time [math]\displaystyle{ (t) }[/math] and latitude ([math]\displaystyle{ \Phi) }[/math] dependent parameters given by:
- [math]\displaystyle{ \xi(\phi,t)=\xi_{_{avg}}(\phi)-\xi_{_{amp}}(\phi) \cos \left ( 2\pi \frac{t-T_0}{365.25} \right ) \qquad\mbox{(4)} }[/math]
where, [math]\displaystyle{ t }[/math] is the time from January [math]\displaystyle{ 0.0 }[/math], in days, and [math]\displaystyle{ T_0 }[/math] is taken as DoY [math]\displaystyle{ 28 }[/math] (i.e., [math]\displaystyle{ T_0=28 }[/math]). The parameters [math]\displaystyle{ \xi_{_{avg}}(\phi_i) }[/math] and [math]\displaystyle{ \xi_{_{amp}}(\phi_i) }[/math] are linearly interpolated from table 1 between the nearest [math]\displaystyle{ \xi(\Phi_i) }[/math]. The [math]\displaystyle{ a_{ht} }[/math], [math]\displaystyle{ b_{ht} }[/math], [math]\displaystyle{ c_{ht} }[/math] are taken directly from the same table 1.
- The wet parameters [math]\displaystyle{ a_w }[/math], [math]\displaystyle{ b_w }[/math], [math]\displaystyle{ c_w }[/math] are latitude dependent and are linearly interpolated from table 2 between the nearest [math]\displaystyle{ \xi(\Phi_i) }[/math].
References
- ^ [Niell, 1996] Niell, A., 1996. Global mapping functions for the atmosphere delay at radio wavelengths. Journal of Geophysical Research. 101, pp. 3227-3246.
- ^ [Marini, 1972] Marini, J., 1972. Correction of Satellite tracking data for an arbitrary Tropospheric Pro_le. Radio Science. 7(2), pp. 223-231.