If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Monitoring Climate Using Ground-based GNSS Measurements: Difference between revisions
m (Created page with "{{Article Infobox2 |Category=Applications |Authors=Tong Ning and Gunnar Elgered - Chalmers University of Technology |Editors=GMV |Level=Advanced |YearOfPublication=2015 |Title={{...") |
mNo edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
Integrated amount of Water Vapour (IWV) in the Earth's atmosphere can be measured by ground-based networks from Global Navigation Satellite Systems (GNSS). The estimated long time series of the IWV can be used as an independent data source to assess possible global warming scenarios and/or evaluate the performance of climate models. | Integrated amount of Water Vapour (IWV) in the Earth's atmosphere can be measured by ground-based networks from Global Navigation Satellite Systems (GNSS). The estimated long time series of the IWV can be used as an independent data source to assess possible global warming scenarios and/or evaluate the performance of climate models. | ||
| Line 19: | Line 16: | ||
Traditionally, radiosondes are used to observe long time series of the IWV <ref>Ross, R.J., and W.P. Elliott, Radiosonde based northern hemisphere tropospheric water vapor trends, J. Climate, 14, 1,602{1,612, doi:10.1175/1520-0442(2001)014<1602:RBNHTW>2.0.CO;2, 2001.</ref>. The limitation of radiosonde data for climate research is that the derived IWV is not homogeneous over long time periods due to calibration uncertainties and sensor changes. A Water Vapour Radiometer (WVR) can also be used to provide IWV estimates <ref>Elgered, G., and P.O.J. Jarlemark, Ground-based microwave radiometry and long-term observations of atmospheric water vapor, Radio Sci., 33, 707{717, doi: 10.1029/98RS00488, 1998.</ref>. However, the WVR has not been proven to be sufficiently stable in terms of determining the long time series of the IWV. Furthermore, the WVR is not a commonly used instrument and it is inaccurate when the drop size is not significantly smaller than the observed wavelength, i.e. during rain. | Traditionally, radiosondes are used to observe long time series of the IWV <ref>Ross, R.J., and W.P. Elliott, Radiosonde based northern hemisphere tropospheric water vapor trends, J. Climate, 14, 1,602{1,612, doi:10.1175/1520-0442(2001)014<1602:RBNHTW>2.0.CO;2, 2001.</ref>. The limitation of radiosonde data for climate research is that the derived IWV is not homogeneous over long time periods due to calibration uncertainties and sensor changes. A Water Vapour Radiometer (WVR) can also be used to provide IWV estimates <ref>Elgered, G., and P.O.J. Jarlemark, Ground-based microwave radiometry and long-term observations of atmospheric water vapor, Radio Sci., 33, 707{717, doi: 10.1029/98RS00488, 1998.</ref>. However, the WVR has not been proven to be sufficiently stable in terms of determining the long time series of the IWV. Furthermore, the WVR is not a commonly used instrument and it is inaccurate when the drop size is not significantly smaller than the observed wavelength, i.e. during rain. | ||
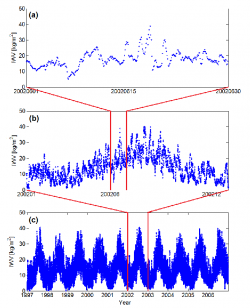
[[File: Iwv_fig1.png|right|thumb|250px]] | [[File: Iwv_fig1.png|right|thumb|250px| Figure 1: The hourly IWV time series, derived from the observations acquired at the IGS site ONSA at the west coast of Sweden, shown for (a) the month of June, 2002, (b) the year of 2002, (c) the time period from January 1997 to December 2006.]] | ||
More recently, based on the path delay when radio waves propagate through the neutral atmosphere of the Earth, the IWV can be inferred from observations acquired from space geodetic techniques, such as GNSS and Very Long Baseline Interferometry (VLBI). The IWV estimated from VLBI observations has a higher accuracy due to that the VLBI antenna has a very high directivity which is less affected by reflected signals from the ground. However, most of the geodetic VLBI sites do not provide continuous measurements and there are less than 150 VLBI telescopes world-wide. The poor temporal and spatial resolutions of the VLBI-derived IWV limit the role of the technique to the calibration of the IWV from co-located GNSS stations. | More recently, based on the path delay when radio waves propagate through the neutral atmosphere of the Earth, the IWV can be inferred from observations acquired from space geodetic techniques, such as GNSS and Very Long Baseline Interferometry (VLBI). The IWV estimated from VLBI observations has a higher accuracy due to that the VLBI antenna has a very high directivity which is less affected by reflected signals from the ground. However, most of the geodetic VLBI sites do not provide continuous measurements and there are less than 150 VLBI telescopes world-wide. The poor temporal and spatial resolutions of the VLBI-derived IWV limit the role of the technique to the calibration of the IWV from co-located GNSS stations. | ||
The method of using observations acquired from ground-based GNSS, e.g. GPS, sites to estimate IWV is widely recognized. GNSS observations from the ground can be made under in principle all weather conditions with a high temporal resolution (up to a few minutes) which is desired to capture short-term variability of the IWV (see Figure). In addition, the number of ground GNSS sites is continuously increasing both globally and regionally. | The method of using observations acquired from ground-based GNSS, e.g. GPS, sites to estimate IWV is widely recognized. GNSS observations from the ground can be made under in principle all weather conditions with a high temporal resolution (up to a few minutes) which is desired to capture short-term variability of the IWV (see Figure 1). In addition, the number of ground GNSS sites is continuously increasing both globally and regionally. | ||
Globally more than 380 sites are used in the International GNSS Service (IGS) as of 1 December, 2014. Since April 2005, Denmark is hosting the EIG EUMETNET GNSS water vapour programme (E-GVAP) to provide EUMETNET members with water vapour estimates for operational meteorology in near real-time. Currently, the E-GVAP network consists of more than 1500 GNSS sites, which are mainly in Europe. | Globally more than 380 sites are used in the International GNSS Service (IGS) as of 1 December, 2014. Since April 2005, Denmark is hosting the EIG EUMETNET GNSS water vapour programme (E-GVAP) to provide EUMETNET members with water vapour estimates for operational meteorology in near real-time. Currently, the E-GVAP network consists of more than 1500 GNSS sites, which are mainly in Europe. | ||
| Line 34: | Line 31: | ||
= Evaluation of climate models = | = Evaluation of climate models = | ||
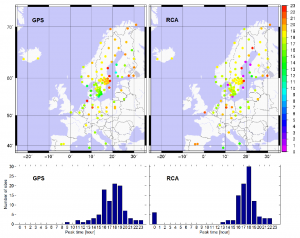
[[File: Iwv_fig2.png|right|thumb|300px]] | [[File: Iwv_fig2.png|right|thumb|300px|Figure 2: Peak time of the diurnal cycle of the IWV, for the summer months (JJA), obtained from the GPS data and the RCA simulation for each GPS site (upper panels) and histograms of the peak time (lower panels). The hour is in local solar time.]] | ||
The Earth's climate system and its changes over time can be simulated by Global Climate Models (GCMs). The simulations of the past and the present are of great importance for us to understand the Earth's climate system and causes for climate change. GCMs are also used to simulate the response of the climate system to current and future changes in radiative forcing <ref>Meehl, G., T. Stocker, W. Collins, and et al., Global climate projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, edited by S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. Averyt, M. Tignor, and H. Miller, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007.</ref>, which are normally referred to as climate feedbacks. As the most important climate feedback, water vapour feedback plays a vital role in the climate system. Therefore, it is desired and required that the IWV simulated by climate models are evaluated using accurate and independent observations. | The Earth's climate system and its changes over time can be simulated by Global Climate Models (GCMs). The simulations of the past and the present are of great importance for us to understand the Earth's climate system and causes for climate change. GCMs are also used to simulate the response of the climate system to current and future changes in radiative forcing <ref>Meehl, G., T. Stocker, W. Collins, and et al., Global climate projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, edited by S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. Averyt, M. Tignor, and H. Miller, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007.</ref>, which are normally referred to as climate feedbacks. As the most important climate feedback, water vapour feedback plays a vital role in the climate system. Therefore, it is desired and required that the IWV simulated by climate models are evaluated using accurate and independent observations. | ||
| Line 40: | Line 37: | ||
Given the advantages we discussed before (high temporal resolution and continuously improved spatial resolution), the GNSS data have a superiority for the evaluation of the IWV over different time scales, e.g. seasonal and diurnal, and on a global scale. In addition, currently the ground-based GNSS data have not yet been assimilated in any climate reanalysis products which makes them an independent data set suitable for the evaluation of climate models. | Given the advantages we discussed before (high temporal resolution and continuously improved spatial resolution), the GNSS data have a superiority for the evaluation of the IWV over different time scales, e.g. seasonal and diurnal, and on a global scale. In addition, currently the ground-based GNSS data have not yet been assimilated in any climate reanalysis products which makes them an independent data set suitable for the evaluation of climate models. | ||
One example of using GNSS-derived IWV to evaluate the ability of climate models to simulate the diurnal cycles of the IWV is shown in the | One example of using GNSS-derived IWV to evaluate the ability of climate models to simulate the diurnal cycles of the IWV is shown in Figure 2<ref>Ning, T., and G. Elgered, Trends in the atmospheric water vapor content from ground-based GPS: the impact of the elevation cutoff angle, IEEE J-STARS, 5(3), doi:10.1109/JSTARS.2012.2191392, 2012.</ref>. The diurnal cycles for 14 consecutive summer months (from 1997 to 2010): June, July, and August, were estimated at 99 sites using the GPS-derived IWV and the simulation from the regional Rossby Centre Atmospheric (RCA) climate model which is developed at the Swedish Meteorological and Hydrological Institute. The result shows a clear positive correlation between GPS and RCA. The time of the maximum varies from 16 to 19 local solar time (LST) for the GPS data while there is a dominant peak at 18 LST for the RCA data. The RCA captures the geographical variations from west to east, with later peaks in the afternoon further to the east. | ||
= Long-term trends in IWV = | = Long-term trends in IWV = | ||
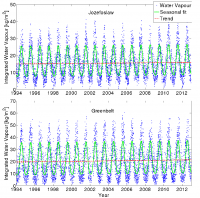
[[File: Iwv_fig3.png|right|thumb|200px]] | [[File: Iwv_fig3.png|right|thumb|200px|Figure 3: The time series of the daily IWV obtained at two GNSS site: Jozefoslaw in Poland and Greehelt in US during 19 years. The blue dots are hourly GNSS observations. Modelling a linear trend (the red line) and seasonal components (the green line). The estimated IWV trends for the two sites are 0.52 kg/(m2.decade) and 0.94 kg/(m2.decade), respectively.]] | ||
Linear trends in the IWV are masked by seasonal variations as well as the variability caused by moving weather systems of dry and wet air masses. In order to estimate linear trends a model can be used that takes the seasonal variants into account: | Linear trends in the IWV are masked by seasonal variations as well as the variability caused by moving weather systems of dry and wet air masses. In order to estimate linear trends a model can be used that takes the seasonal variants into account: | ||
| Line 52: | Line 49: | ||
where I is the IWV and t is the time in years. The parameters I<sub>0</sub> and a<sub>1</sub> are the mean offset and the linear trend of the IWV, respectively; a<sub>2</sub> and a<sub>3</sub> describe the annual component, and a<sub>4</sub> and a<sub>5</sub> describe the semi-annual component. | where I is the IWV and t is the time in years. The parameters I<sub>0</sub> and a<sub>1</sub> are the mean offset and the linear trend of the IWV, respectively; a<sub>2</sub> and a<sub>3</sub> describe the annual component, and a<sub>4</sub> and a<sub>5</sub> describe the semi-annual component. | ||
All these coefficients are determined through the method of least squares. Two examples of the IWV time series and estimated linear trends obtained from GNSS observations are shown in | All these coefficients are determined through the method of least squares. Two examples of the IWV time series and estimated linear trends obtained from GNSS observations are shown in Figure 3 for two sites: Jozefoslaw (21.03 °E, 52.10 °N) in Poland and Greenbelt (-76.83 °E, 39.02 °N) in the US. Using 19 years (1994 to 2012) of data, the estimated IWV trends for the two sites are 0.52 <math>kg/(m^2 . decade)</math> and 0.94 <math>kg/(m^2 . decade)</math>, respectively. | ||
| Line 58: | Line 55: | ||
In order to properly interpret the IWV trends derived from GNSS observations, the uncertainty of the trend needs to be addressed. It is determined by the length of the IWV time series, the magnitude of the formal error of the individual IWV value, and the short-term variations in the IWV. In addition, the IWV trend maybe be affected by sudden changes in the GNSS data, e.g. instrument replacements and changes of the electromagnetic environment around the antenna. | In order to properly interpret the IWV trends derived from GNSS observations, the uncertainty of the trend needs to be addressed. It is determined by the length of the IWV time series, the magnitude of the formal error of the individual IWV value, and the short-term variations in the IWV. In addition, the IWV trend maybe be affected by sudden changes in the GNSS data, e.g. instrument replacements and changes of the electromagnetic environment around the antenna. | ||
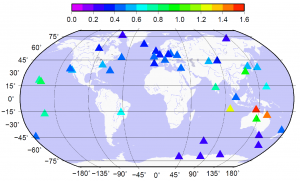
[[File: Iwv_fig4.png|left|thumb|300px]] | [[File: Iwv_fig4.png|left|thumb|300px|Figure 4: Linear IWV trends estimated for 42 global GNSS sites for the time period from 1 January 1997 to 31 December 2011. The red circles mean positive trends and the blue circles mean negative trends. The size of the circle is proportional the value of the trend as indicated in Figure 4. The trends are in the range from -1.65 kg/(m2.decade) to 2.32 kg/(m2.decade).]] | ||
The trend uncertainty can be quantified using statistical models. If we assume that the IWV formal errors are white noise, the calculated trend uncertainty can be as low as 0.03 <math>kg/(m^2 . decade)</math> for 14 years of data <ref>Ning, T., and G. Elgered, Trends in the atmospheric water vapor content from ground-based GPS: the impact of the elevation cutoff angle, IEEE J-STARS, 5(3), doi:10.1109/JSTARS.2012.2191392, 2012.</ref>. This uncertainty, however, only gives information on how the estimated trend differs from what would be estimated if the IWV did not contain deviations from the model other than white noise. In order to address the trend significance, the true short-term variation in the IWV, which can be of time scales from days up to several months and is not modelled by the equation in the previous section, needs to be taken into account. Using 10 years of data from 33 GNSS sites in Finland and Sweden, <ref>Nilsson, T., and G. Elgered, Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data, J. Geophys. Res., 113, D19101, doi:10. 1029/2008JD010110, 2008.</ref> found that the trend uncertainty, after taking the temporal correlation of the variation about the estimated model into account, are of the order of 0.4 <math>kg/(m^2 . decade)</math>. | The trend uncertainty can be quantified using statistical models. If we assume that the IWV formal errors are white noise, the calculated trend uncertainty can be as low as 0.03 <math>kg/(m^2 . decade)</math> for 14 years of data <ref>Ning, T., and G. Elgered, Trends in the atmospheric water vapor content from ground-based GPS: the impact of the elevation cutoff angle, IEEE J-STARS, 5(3), doi:10.1109/JSTARS.2012.2191392, 2012.</ref>. This uncertainty, however, only gives information on how the estimated trend differs from what would be estimated if the IWV did not contain deviations from the model other than white noise. In order to address the trend significance, the true short-term variation in the IWV, which can be of time scales from days up to several months and is not modelled by the equation in the previous section, needs to be taken into account. Using 10 years of data from 33 GNSS sites in Finland and Sweden, <ref>Nilsson, T., and G. Elgered, Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data, J. Geophys. Res., 113, D19101, doi:10. 1029/2008JD010110, 2008.</ref> found that the trend uncertainty, after taking the temporal correlation of the variation about the estimated model into account, are of the order of 0.4 <math>kg/(m^2 . decade)</math>. | ||
[[File: Iwv_fig5.png|right|thumb|300px]] | [[File: Iwv_fig5.png|right|thumb|300px|Figure 5: Uncertainties of the IWV trends for all the sites, which are presented in Figure 4, after taking short-term variations into account. The uncertainties vary from 0.21 kg/(m2.decade) to 1.52 kg/(m2.decade).]] | ||
An example of the effect by a sudden change in the GNSS data has occurred at the IGS site ONSA at the west coast of Sweden, where a radome change was made on 1 February 1999. The change introduced an offset of 0.4 <math>kg/(m^2 . decade)</math> in the IWV <ref>Gradinarsky, L.P., J.M. Johansson, H.R. Bouma, H.-G. Scherneck, and G. Elgered, Climate monitoring using GPS, Phys. Chem. Earth, 27, 225{340, doi:10.1016/S1474-7065(02)00009-8, 2002.</ref>. After the correction for the offset, the linear trend estimated from a 14 years data for ONSA changes from -0.2 <math>kg/(m^2 . decade)</math> to +0.2 <math>kg/(m^2 . decade)</math>. | An example of the effect by a sudden change in the GNSS data has occurred at the IGS site ONSA at the west coast of Sweden, where a radome change was made on 1 February 1999. The change introduced an offset of 0.4 <math>kg/(m^2 . decade)</math> in the IWV <ref>Gradinarsky, L.P., J.M. Johansson, H.R. Bouma, H.-G. Scherneck, and G. Elgered, Climate monitoring using GPS, Phys. Chem. Earth, 27, 225{340, doi:10.1016/S1474-7065(02)00009-8, 2002.</ref>. After the correction for the offset, the linear trend estimated from a 14 years data for ONSA changes from -0.2 <math>kg/(m^2 . decade)</math> to +0.2 <math>kg/(m^2 . decade)</math>. | ||
| Line 68: | Line 65: | ||
In conclusion, due to the relative short time period of the GNSS-derived IWV (< 20 years), the short-term variations dominate the uncertainty of the estimated linear trends. It should also be pointed out that the impact from the systematic error due to the changes related to an instrument or the antenna environment cannot be ignored. Corrections of such errors are necessary for a reliable trend estimation. | In conclusion, due to the relative short time period of the GNSS-derived IWV (< 20 years), the short-term variations dominate the uncertainty of the estimated linear trends. It should also be pointed out that the impact from the systematic error due to the changes related to an instrument or the antenna environment cannot be ignored. Corrections of such errors are necessary for a reliable trend estimation. | ||
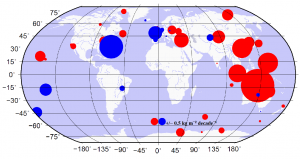
A final example of globally estimated IWV trends is shown in | A final example of globally estimated IWV trends is shown in Figure 4 where the trends are in the range from -1.65 <math>kg/(m^2 . decade)</math> to 2.32 <math>kg/(m^2 . decade)</math> for 42 globally distributed GNSS sites and for a 15 years data. After taking the short-term variations into account, the corresponding trend uncertainties vary from 0.21 <math>kg/(m^2 . decade)</math> to 1.52 <math>kg/(m^2 . decade)</math> (see Figure 5). | ||
| Line 75: | Line 72: | ||
[[Category:Applications]] | [[Category:Applications]] | ||
[[Category:Scientific Applications]] | |||
Latest revision as of 14:34, 28 January 2015
| Applications | |
|---|---|
| Title | Monitoring Climate Using Ground-based GNSS Measurements |
| Author(s) | Tong Ning and Gunnar Elgered - Chalmers University of Technology |
| Edited by | GMV |
| Level | Advanced |
| Year of Publication | 2015 |
Integrated amount of Water Vapour (IWV) in the Earth's atmosphere can be measured by ground-based networks from Global Navigation Satellite Systems (GNSS). The estimated long time series of the IWV can be used as an independent data source to assess possible global warming scenarios and/or evaluate the performance of climate models.
Water vapour is one state of water within the hydrospheric cycle through which water vapour constantly enters the atmosphere by evaporation, forms clouds by condensation, and subsequently comes back to the Earth's surface by precipitation [1]. The movement of water vapour is strongly coupled to redistribution of the energy and thus has a significant impact on the climate system. Since the whole water cycle is regulated by the temperature, global warming will have an impact on it. Assuming conservation of relative humidity, the changes in the atmospheric water vapour are related to a change in the temperature with a ratio of approximately 7%/K [2]. Therefore, monitoring long-term changes of the IWV is of great importance for climate research.
Techniques for the long-term IWV estimation
Traditionally, radiosondes are used to observe long time series of the IWV [3]. The limitation of radiosonde data for climate research is that the derived IWV is not homogeneous over long time periods due to calibration uncertainties and sensor changes. A Water Vapour Radiometer (WVR) can also be used to provide IWV estimates [4]. However, the WVR has not been proven to be sufficiently stable in terms of determining the long time series of the IWV. Furthermore, the WVR is not a commonly used instrument and it is inaccurate when the drop size is not significantly smaller than the observed wavelength, i.e. during rain.
More recently, based on the path delay when radio waves propagate through the neutral atmosphere of the Earth, the IWV can be inferred from observations acquired from space geodetic techniques, such as GNSS and Very Long Baseline Interferometry (VLBI). The IWV estimated from VLBI observations has a higher accuracy due to that the VLBI antenna has a very high directivity which is less affected by reflected signals from the ground. However, most of the geodetic VLBI sites do not provide continuous measurements and there are less than 150 VLBI telescopes world-wide. The poor temporal and spatial resolutions of the VLBI-derived IWV limit the role of the technique to the calibration of the IWV from co-located GNSS stations.
The method of using observations acquired from ground-based GNSS, e.g. GPS, sites to estimate IWV is widely recognized. GNSS observations from the ground can be made under in principle all weather conditions with a high temporal resolution (up to a few minutes) which is desired to capture short-term variability of the IWV (see Figure 1). In addition, the number of ground GNSS sites is continuously increasing both globally and regionally.
Globally more than 380 sites are used in the International GNSS Service (IGS) as of 1 December, 2014. Since April 2005, Denmark is hosting the EIG EUMETNET GNSS water vapour programme (E-GVAP) to provide EUMETNET members with water vapour estimates for operational meteorology in near real-time. Currently, the E-GVAP network consists of more than 1500 GNSS sites, which are mainly in Europe.
The long time series of the IWV obtained from the GNSS data is used in two different climate applications:
- 1. to evaluate the IWV obtained from numerical weather models in climate research.
- 2. To monitor long term variability, e.g. linear trends and diurnal cycles, of the IWV at specific sites.
Evaluation of climate models
The Earth's climate system and its changes over time can be simulated by Global Climate Models (GCMs). The simulations of the past and the present are of great importance for us to understand the Earth's climate system and causes for climate change. GCMs are also used to simulate the response of the climate system to current and future changes in radiative forcing [5], which are normally referred to as climate feedbacks. As the most important climate feedback, water vapour feedback plays a vital role in the climate system. Therefore, it is desired and required that the IWV simulated by climate models are evaluated using accurate and independent observations.
Given the advantages we discussed before (high temporal resolution and continuously improved spatial resolution), the GNSS data have a superiority for the evaluation of the IWV over different time scales, e.g. seasonal and diurnal, and on a global scale. In addition, currently the ground-based GNSS data have not yet been assimilated in any climate reanalysis products which makes them an independent data set suitable for the evaluation of climate models.
One example of using GNSS-derived IWV to evaluate the ability of climate models to simulate the diurnal cycles of the IWV is shown in Figure 2[6]. The diurnal cycles for 14 consecutive summer months (from 1997 to 2010): June, July, and August, were estimated at 99 sites using the GPS-derived IWV and the simulation from the regional Rossby Centre Atmospheric (RCA) climate model which is developed at the Swedish Meteorological and Hydrological Institute. The result shows a clear positive correlation between GPS and RCA. The time of the maximum varies from 16 to 19 local solar time (LST) for the GPS data while there is a dominant peak at 18 LST for the RCA data. The RCA captures the geographical variations from west to east, with later peaks in the afternoon further to the east.
Long-term trends in IWV
Linear trends in the IWV are masked by seasonal variations as well as the variability caused by moving weather systems of dry and wet air masses. In order to estimate linear trends a model can be used that takes the seasonal variants into account:
[math]\displaystyle{ I=I_0+a_1t+a_2sin(2 \pi t)+a_3cos(2 \pi t)+a_4sin(4 \pi t)+a_5cos(4 \pi t) }[/math]
where I is the IWV and t is the time in years. The parameters I0 and a1 are the mean offset and the linear trend of the IWV, respectively; a2 and a3 describe the annual component, and a4 and a5 describe the semi-annual component.
All these coefficients are determined through the method of least squares. Two examples of the IWV time series and estimated linear trends obtained from GNSS observations are shown in Figure 3 for two sites: Jozefoslaw (21.03 °E, 52.10 °N) in Poland and Greenbelt (-76.83 °E, 39.02 °N) in the US. Using 19 years (1994 to 2012) of data, the estimated IWV trends for the two sites are 0.52 [math]\displaystyle{ kg/(m^2 . decade) }[/math] and 0.94 [math]\displaystyle{ kg/(m^2 . decade) }[/math], respectively.
Uncertainty of the estimated IWV trend
In order to properly interpret the IWV trends derived from GNSS observations, the uncertainty of the trend needs to be addressed. It is determined by the length of the IWV time series, the magnitude of the formal error of the individual IWV value, and the short-term variations in the IWV. In addition, the IWV trend maybe be affected by sudden changes in the GNSS data, e.g. instrument replacements and changes of the electromagnetic environment around the antenna.
The trend uncertainty can be quantified using statistical models. If we assume that the IWV formal errors are white noise, the calculated trend uncertainty can be as low as 0.03 [math]\displaystyle{ kg/(m^2 . decade) }[/math] for 14 years of data [7]. This uncertainty, however, only gives information on how the estimated trend differs from what would be estimated if the IWV did not contain deviations from the model other than white noise. In order to address the trend significance, the true short-term variation in the IWV, which can be of time scales from days up to several months and is not modelled by the equation in the previous section, needs to be taken into account. Using 10 years of data from 33 GNSS sites in Finland and Sweden, [8] found that the trend uncertainty, after taking the temporal correlation of the variation about the estimated model into account, are of the order of 0.4 [math]\displaystyle{ kg/(m^2 . decade) }[/math].
An example of the effect by a sudden change in the GNSS data has occurred at the IGS site ONSA at the west coast of Sweden, where a radome change was made on 1 February 1999. The change introduced an offset of 0.4 [math]\displaystyle{ kg/(m^2 . decade) }[/math] in the IWV [9]. After the correction for the offset, the linear trend estimated from a 14 years data for ONSA changes from -0.2 [math]\displaystyle{ kg/(m^2 . decade) }[/math] to +0.2 [math]\displaystyle{ kg/(m^2 . decade) }[/math].
In conclusion, due to the relative short time period of the GNSS-derived IWV (< 20 years), the short-term variations dominate the uncertainty of the estimated linear trends. It should also be pointed out that the impact from the systematic error due to the changes related to an instrument or the antenna environment cannot be ignored. Corrections of such errors are necessary for a reliable trend estimation.
A final example of globally estimated IWV trends is shown in Figure 4 where the trends are in the range from -1.65 [math]\displaystyle{ kg/(m^2 . decade) }[/math] to 2.32 [math]\displaystyle{ kg/(m^2 . decade) }[/math] for 42 globally distributed GNSS sites and for a 15 years data. After taking the short-term variations into account, the corresponding trend uncertainties vary from 0.21 [math]\displaystyle{ kg/(m^2 . decade) }[/math] to 1.52 [math]\displaystyle{ kg/(m^2 . decade) }[/math] (see Figure 5).
References
- ^ Bengtsson, L., The global atmospheric water cycle, Environ. Res. Lett., 109, doi:10.1088/1748-9326/5/2/025002, 2010.
- ^ Trenberth, K.E., A. Dai, R.M. Rasmussen, and D.B. Parsons, The changing character of precipitation, Bull Amer Meteor Soc., 84(9), 1,205{1,217, doi:10.1175/BAMS-84-9-1205, 2003.
- ^ Ross, R.J., and W.P. Elliott, Radiosonde based northern hemisphere tropospheric water vapor trends, J. Climate, 14, 1,602{1,612, doi:10.1175/1520-0442(2001)014<1602:RBNHTW>2.0.CO;2, 2001.
- ^ Elgered, G., and P.O.J. Jarlemark, Ground-based microwave radiometry and long-term observations of atmospheric water vapor, Radio Sci., 33, 707{717, doi: 10.1029/98RS00488, 1998.
- ^ Meehl, G., T. Stocker, W. Collins, and et al., Global climate projections. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, edited by S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. Averyt, M. Tignor, and H. Miller, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2007.
- ^ Ning, T., and G. Elgered, Trends in the atmospheric water vapor content from ground-based GPS: the impact of the elevation cutoff angle, IEEE J-STARS, 5(3), doi:10.1109/JSTARS.2012.2191392, 2012.
- ^ Ning, T., and G. Elgered, Trends in the atmospheric water vapor content from ground-based GPS: the impact of the elevation cutoff angle, IEEE J-STARS, 5(3), doi:10.1109/JSTARS.2012.2191392, 2012.
- ^ Nilsson, T., and G. Elgered, Long-term trends in the atmospheric water vapor content estimated from ground-based GPS data, J. Geophys. Res., 113, D19101, doi:10. 1029/2008JD010110, 2008.
- ^ Gradinarsky, L.P., J.M. Johansson, H.R. Bouma, H.-G. Scherneck, and G. Elgered, Climate monitoring using GPS, Phys. Chem. Earth, 27, 225{340, doi:10.1016/S1474-7065(02)00009-8, 2002.