If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
RTK Fundamentals: Difference between revisions
m (→RTK Algorithm) |
|||
| Line 64: | Line 64: | ||
===Ambiguity Resolution=== | ===Ambiguity Resolution=== | ||
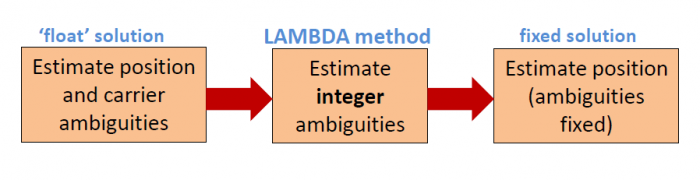
As it was said above the ambiguity resolution is the key of positioning precision in RTK Technique. It can be divided in mainly three steps, as shown in the figure. | |||
[[File:LambdaMethod.PNG|700px|center]] | |||
The first step is an "ordinary" least-squares, that can be done either in a batch implementation or a Kalman filter. In this process the integer nature of the ambiguities is not considered, and therefore, the solution of the process are real-valued estimates; the so-called 'float' solution, that includes baseline coordinates, differential atmospheric delays and carrier phase ambiguities.<ref name="GPS_WORLD_LAMBDA">[http://chromatographyonline.findanalytichem.com/lcgc/article/articleDetail.jsp?id=584852&sk=&date=&pageID=3 Bernd Eissfeller, Thomas Pany, Günter Heinrichs, Christian Tiberius, ''Real-Time Kinematic in the Light of GPS Modernization and Galileo'', Oct. 1, 2002, GPS Word]</ref> | |||
The second step is the LAMBDA method itself <ref>[http://enterprise.lr.tudelft.nl/publications/files/PT_BEIJING93.PDF ''Least-Squares Estimation of the Integer GPS Ambiguities''] by P. Teunissen, 1993.</ref><ref>[http://enterprise.lr.tudelft.nl/publications/files/Teunissen_JoG_1995_V70N1-2.pdf ''The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation''] by P. Teunissen, 1995.</ref><ref>[http://enterprise.lr.tudelft.nl/publications/files/lgr12.pdf ''The LAMBDA method for integer ambiguity estimation: implementation aspects''] by P. de Jonge and C. Tiberius, 1996.</ref> , developed by [http://lr.tudelft.nl/index.php?id=26369&L=1 Delft University of Technology]. It consists mainly in the decorrelation of the ambiguities, taking into account their integer nature. This decorrelation lets to a fast and efficiently integer least-squares computation.<ref name="TU_Delf_Lambda">[http://lr.tudelft.nl/index.php?id=26369&L=1 Lambda Method homepage by Delft University of Technology.]</ref> | |||
Finally, in the last step, the solution of the remaining parameters, i.e. the baseline coordinates and additional parameters such as atmospheric delays, is computed keeping the ambiguities fixed to the integer values obtained in second step. This final solution is known as the "fixed" solution and the obtained values generally have centimeter level precision or less.<ref name="GPS_WORLD_LAMBDA"/> <ref name="TU_Delf_Lambda"/> | |||
The integer least-squares principle embodied in the LAMBDA method has been demonstrated to be optimal. The integer least-squares estimator is best in the sense of maximizing the probability of correct integer estimation, i.e. in maximizing the ambiguity success-rate. This measure expresses, given a certain scenario, how successful one can expect to be in resolving the integer carrier phase ambiguities correctly. The ambiguity success-rate - a statistical probability - is a number between 0 and 1 (to be interpreted as 0 percent and 100 percent, respectively). As an exact evaluation of this success-rate is complicated in the context of integer least-squares estimation, therefore an approximation is used, based on so-called bootstrapping. The bootstrap success-rate is a guaranteed (and hence safe) lower bound for the success-rate; the actual integer least-squares success-rate will be larger than, or at least be equal to, the value given.<ref name="GPS_WORLD_LAMBDA"/> | The integer least-squares principle embodied in the LAMBDA method has been demonstrated to be optimal. The integer least-squares estimator is best in the sense of maximizing the probability of correct integer estimation, i.e. in maximizing the ambiguity success-rate. This measure expresses, given a certain scenario, how successful one can expect to be in resolving the integer carrier phase ambiguities correctly. The ambiguity success-rate - a statistical probability - is a number between 0 and 1 (to be interpreted as 0 percent and 100 percent, respectively). As an exact evaluation of this success-rate is complicated in the context of integer least-squares estimation, therefore an approximation is used, based on so-called bootstrapping. The bootstrap success-rate is a guaranteed (and hence safe) lower bound for the success-rate; the actual integer least-squares success-rate will be larger than, or at least be equal to, the value given.<ref name="GPS_WORLD_LAMBDA"/> | ||
Revision as of 17:32, 8 November 2011
| Fundamentals | |
|---|---|
| Title | RTK Fundamentals |
| Author(s) | See Credits section |
| Level | Basic |
| Year of Publication | 2011 |
Real Time Kinematic (RTK) satellite navigation is a DGNSS technique used in land survey and in hydrographic survey based on the use of carrier phase measurements of the GPS, GLONASS and/or Galileo signals where a single reference station provides the real-time corrections, providing up to centimeter-level accuracy. When referring to GPS in particular, the system is also commonly referred to as Carrier-Phase Enhancement, CPGPS.[1]
RTK Technique
The classical GNSS receivers compare a C/A code pseudoranges signal being sent from the satellite with an internally generated copy of the same signal. Since the signal from the satellite takes time to reach the receiver, the two signals do not "line up" properly; the satellite's copy is delayed in relation to the local copy. By progressively delaying the local copy more and more, the two signals will eventually line up properly. That delay is the time needed for the signal to reach the receiver, and from this the distance from the satellite can be calculated.[1]
The accuracy of the resulting range measurement is generally a function of the ability of the receiver's electronics to accurately compare the two signals. In general receivers are able to align the signals to about 1% of one bit-width. For instance, the coarse-acquisition (C/A) code sent on the GPS system sends a bit every 0.98 microsecond, so a receiver is accurate to 0.01 microsecond, or about 3 metres in terms of distance. The military-only P(Y) signal sent by the same satellites is clocked ten times as fast, so with similar techniques the receiver will be accurate to about 30 cm. Other effects introduce errors much greater than this, and accuracy based on an uncorrected C/A signal is generally about 15 m.[1]
RTK follows the same general concept, but uses the satellite's carrier phase as its signal, not the messages contained within. The improvement possible using this signal is potentially very high if one continues to assume a 1% accuracy in locking. For instance, the GPS coarse-acquisition (C/A) code broadcast in the L1 signal changes phase at 1.023 MHz, but the L1 carrier itself is 1575.42 MHz, over a thousand times as fast. This frequency corresponds to a wavelength of 19 cm for the L1 signal. Thus a ±1% error in L1 carrier phase measurement corresponds to a ±1.9mm error in baseline estimation.[1]
RTK Algorithm
The difficulty in making an RTK system is properly aligning the signals.[1] As stated in Septentrio homepage, the carrier phase measurements are extremely precise (down to the fractions of millimeter), but they contain an unknown integer initialization constant, the so-called “phase ambiguity”. Therefore RTK positioning has to resolve integer ambiguities to achieve the high level of precision.[2]
The RTK Algorithm is based on double differenced observables that can eliminate selective availability effects as well as other biases. The highlights of the algorithm are described next. At a given epoch, and for a given satellite, the simplified carrier phase observation equation is the following:
[math]\displaystyle{ \qquad \phi =\rho-I+Tr+c(b_{Rx}-b_{Sat} )+〖N\lambda+\varepsilon〗_\phi \qquad \mbox{(1)} }[/math]
Where:
[math]\displaystyle{ I }[/math] is the signal path delay due to the ionosphere;
[math]\displaystyle{ Tr }[/math] is the signal path delay due to the troposphere;
[math]\displaystyle{ b_{Rx} }[/math] is the receiver clock offset from the reference (GPS) time;
[math]\displaystyle{ b_{Sat} }[/math] is the satellite clock offset from the reference (GPS) time;
[math]\displaystyle{ c }[/math] is the vacuum speed of light;
[math]\displaystyle{ \lambda }[/math] is the carrier nominal wavelength;
[math]\displaystyle{ N }[/math] is the ambiguity of the carrier-phase (integer number);
[math]\displaystyle{ \varepsilon_\phi }[/math] are the measurement noise components, including multipath and other effects;
[math]\displaystyle{ \rho }[/math] is the geometrical range between the satellite and the receiver, computed as a function of the satellite [math]\displaystyle{ (x_{Sat}, y_{Sat},z_{Sat}) }[/math] and receiver [math]\displaystyle{ (x_{Rx}, y_{Rx},z_{Rx}) }[/math] coordinates as:
[math]\displaystyle{ \qquad \rho=\sqrt{〖(x_{Sat}-x_{Rx})〗^2+〖(y_{Sat}-y_{Rx})〗^2+〖(z_{Sat}-z_{Rx})〗^2 } \qquad \mbox{(2)} }[/math].
For two receivers a and b making simultaneous measurements at the same nominal time to satellites 1 and 2, the double difference observable is:
[math]\displaystyle{ \qquad \phi_a^{12} - \phi_b^{12} =\rho_a^{12}-\rho_b^{12}-I_a^{12}+I_b^{12}+Tr_a^{12}-Tr_b^{12}+\lambda(N_a^{12}-N_b^{12})+\varepsilon_a^{12}- \varepsilon_b^{12} \qquad \mbox{(3)} }[/math]
In the above equation receiver and satellite clock offsets and hardware biases cancel, since double differencing is effectively differencing between satellites and between receivers. The single difference ambiguities difference [math]\displaystyle{ N_a^{12}-N_b^{12} }[/math] is commonly parameterized as a new ambiguity parameter [math]\displaystyle{ N_a^{12} }[/math]. The advantage of double differencing is that the new ambiguity parameter [math]\displaystyle{ N_a^{12} }[/math] is an integer because the non-integer terms in the GPS carrier phase observation, due to clock and hardware delays in the transmitter and receiver, are eliminated.
Between the different challenges to achieve the high level of precision, i.e. cm-level positioning, there are two:
- The compensation of atmospheric effects is not complete and the induced errors increase with the baseline distance due to error decorrelation. For baselines of more than 15-20 km, ambiguity fixing is less reliable during periods of high ionospheric activity. There exist a number of so-called Network RTK techniques, where information from a network of base stations is used to better predict the variations of ionosphere delays and orbit errors.
- Resolve the unknown integer ambiguities of the double-differenced carrier phase observables. This process is referred to as Integer Ambiguity Resolution and is the key in RTK algorithm.
Ambiguity Resolution
As it was said above the ambiguity resolution is the key of positioning precision in RTK Technique. It can be divided in mainly three steps, as shown in the figure.
The first step is an "ordinary" least-squares, that can be done either in a batch implementation or a Kalman filter. In this process the integer nature of the ambiguities is not considered, and therefore, the solution of the process are real-valued estimates; the so-called 'float' solution, that includes baseline coordinates, differential atmospheric delays and carrier phase ambiguities.[3]
The second step is the LAMBDA method itself [4][5][6] , developed by Delft University of Technology. It consists mainly in the decorrelation of the ambiguities, taking into account their integer nature. This decorrelation lets to a fast and efficiently integer least-squares computation.[7]
Finally, in the last step, the solution of the remaining parameters, i.e. the baseline coordinates and additional parameters such as atmospheric delays, is computed keeping the ambiguities fixed to the integer values obtained in second step. This final solution is known as the "fixed" solution and the obtained values generally have centimeter level precision or less.[3] [7]
The integer least-squares principle embodied in the LAMBDA method has been demonstrated to be optimal. The integer least-squares estimator is best in the sense of maximizing the probability of correct integer estimation, i.e. in maximizing the ambiguity success-rate. This measure expresses, given a certain scenario, how successful one can expect to be in resolving the integer carrier phase ambiguities correctly. The ambiguity success-rate - a statistical probability - is a number between 0 and 1 (to be interpreted as 0 percent and 100 percent, respectively). As an exact evaluation of this success-rate is complicated in the context of integer least-squares estimation, therefore an approximation is used, based on so-called bootstrapping. The bootstrap success-rate is a guaranteed (and hence safe) lower bound for the success-rate; the actual integer least-squares success-rate will be larger than, or at least be equal to, the value given.[3]
The LAMBDA method, the second step in figure, is a separate, generally applicable module for integer estimation, no matter the number of GNSS frequencies and no matter the absence of pseudorange code measurements on a particular frequency or incidentally missing measurements for some of the satellites. The TU Delft University can provide Matlab and Fortran 77 source code of the subroutines for the LAMBDA method.[3]
RTK on-going Research
As stated in the article Introduction to Network RTK:[8]
In recent years first-generation Network RTK services have been developed and they have been established in several countries. These services have proven the practical feasibility of the Network RTK technique and they gained wide acceptance by the user community. Network RTK is emerging as the leading method for precise satellite-based positioning. Based on these experiences the development of second-generation Network RTK systems is under way which will make use of improved algorithms and new transmission standards. A wide range of ongoing and anticipated research is related to Network RTK. Research topics are:
- hierarchical network design: the contribution of global and regional real-time networks to small-scale Network RTK services
- content and format of Network RTK correction messages: Virtual Reference Station (VRS) concept versus broadcast Network RTK concepts
- substitution of observation corrections (RTK) by state space information (PPP – Precise Point Positioning)
- improvement of algorithms for the prediction of atmospheric corrections
- mitigation of station-dependent errors (mainly multipath) at the reference stations
- development of quality indicators for network RTK corrections either from the correction computation itself or based on the observations of additional monitor sites
- new data communication systems (e.g. internet-based, or Digital Audio Broadcast)
- inclusion of the future third GPS frequency and the future Galileo system
- extraction and processing of Network RTK by-products: tropospheric and ionospheric delays, local crustal deformations.
Credits
Edited by GMV. The text in the introduction and the section RTK Technique is mostly taken from Wikipedia with minor adaptation,[1] provided under Creative Commons Attribution-ShareAlike License.
The section Ambiguity Resolution has been taken from the article Real-Time Kinematic in the Light of GPS Modernization and Galileo[3]
The section RTK on-going Research has been taken from the article Introduction to Network RTK.[8]
Notes
References
- ^ a b c d e f RTK in Wikipedia
- ^ DGPS vs RTK, Septentrio
- ^ a b c d e Bernd Eissfeller, Thomas Pany, Günter Heinrichs, Christian Tiberius, Real-Time Kinematic in the Light of GPS Modernization and Galileo, Oct. 1, 2002, GPS Word
- ^ Least-Squares Estimation of the Integer GPS Ambiguities by P. Teunissen, 1993.
- ^ The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation by P. Teunissen, 1995.
- ^ The LAMBDA method for integer ambiguity estimation: implementation aspects by P. de Jonge and C. Tiberius, 1996.
- ^ a b Lambda Method homepage by Delft University of Technology.
- ^ a b Introduction to Network RTK , International Association of Geodesy (IAG) Working Group 4.5.1: Network RTK