An intuitive approach to the GNSS positioning

The basic observable in a GNSS system is the time required for a signal to travel from the satellite (transmitter) to the receiver. This travelling time, multiplied by the speed of light, provides a measure of the apparent distance (pseudo range) between them. The following example summarises, for a two-dimensional case, the basic ideas involved in the GNSS positioning:

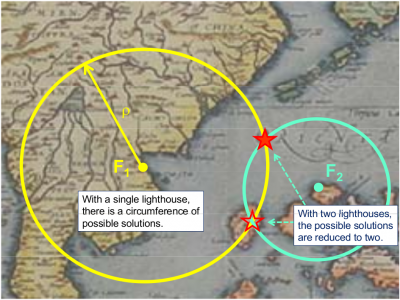
Let's suppose that a lighthouse is emitting acoustic signals at regular intervals of 10 minutes and intense enough to be heard some kilometres away. Let's also assume a ship with a clock perfectly synchronised with the one in the lighthouse, receiving these signals at a time not being an exact multiple of 10 minutes, for example, 20 seconds later [math]\displaystyle{ \left (t = n * 10^m + 20^s \right) }[/math] These 20 seconds will correspond to the propagation time of sound from the lighthouse (transmitter) to the ship (receiver). The distance ρ between them can be obtained multiplying this value by the speed of sound [math]\displaystyle{ v \simeq 335 m/s }[/math]. That is, ρ = 20 s * 335 m/s = 6.7 km. Obviously, with a single lighthouse it is only possible to determine a single measure of distance. So, the ship could be at any point over a circle of radius ρ, see figure 1.1.

With a second lighthouse, the ship position will be given by the intersection of the two circumferences centred in the two lighthouses and radius determined by their distances to the ship (measured using the acoustic signals). In this case, the ship could be situated at any of the two points of intersection shown in figure 1.1. A third lighthouse will solve the previous ambiguity, nevertheless a rough knowledge of the ship position may allow us to proceed without the third lighthouse. For instance, in figure 1.1, one of the solutions falls on the ground (on an island).

Figure 1.1: 2D positioning: With a single lighthouse, there is a circumference of possible ship locations. With two lighthouses, the possible solutions are reduced to two. In the figure one of them can be ruled out because it falls on an island.

A deeper analysis of a 2-D pseudorange based positioning

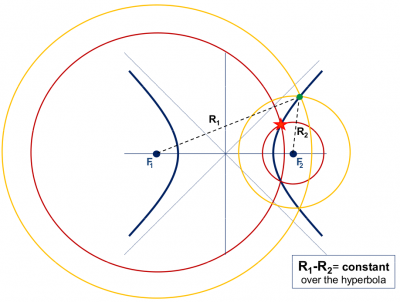
Right now, a perfect synchronism between lighthouses and ship clocks has been assumed, but in fact this is very difficult to assure. Notice that a synchronism error between these clocks will produce an erroneous measure of signal propagation time (because it is linked to such clocks) and, in consequence, an error in the range measurements. Let's assume that the ship clock is biased by an offset dτ regarding the lighthouses clocks (which are supposed to be fully synchronised). Thence, the measured ranges, R1 and R2, will be shifted by an amount [math]\displaystyle{ dt = v.d \tau }[/math]:

[math]\displaystyle{ R_1 = \rho_1 + dt,\space R_2 = \rho_2 + dt }[/math]

That is, the radius of the circles of figure 1.1 will vary by an unknown amount dτ, see figure 1.2. From hereafter we will call Ri as pseudorange, because it contains an unknown error dτ. At first glance, it might seem that the intersection of these circles (with an undefined radius Ri) could reach any point on the plane (for an arbitrary dτ value). However, they will only intersect on the branches of a hyperbola, whose foci are located at the two lighthouses, see figure 1.2. Indeed, as the clock offset dτ cancels when differencing the pseudoranges, the possible ship locations must verify the following equation (which defines an hyperbola, see figure 1.2):

Figure 1.2: An (unknown) offset dτ in the ship's clock produces a shift in the measured ranges (Ri = �i + dt) (or pseudoranges), varying the circumference radius. But, as both pseudoranges R1 and R2 have been measured with the same clock, this offset cancels on the difference of ranges R1 􀀀R2 = �1 􀀀�2 = ctt. Thence, the ship is located at a branch of the hyperbola R1 􀀀 R2 = ctt.