If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
An intuitive approach to the GNSS positioning: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 4: | Line 4: | ||
Let's suppose that a lighthouse is emitting acoustic signals at regular intervals of 10 minutes and intense enough to be heard some kilometres away. Let's also assume a ship with a clock perfectly synchronised with the one in the lighthouse, receiving these signals at a time not being an exact multiple of 10 minutes, for | Let's suppose that a lighthouse is emitting acoustic signals at regular intervals of 10 minutes and intense enough to be heard some kilometres away. Let's also assume a ship with a clock perfectly synchronised with the one in the lighthouse, receiving these signals at a time not being an exact multiple of 10 minutes, for | ||
example, 20 seconds later <math>\left (t = n * 10^m + 20^s \right)</math> | example, 20 seconds later <math>\left (t = n * 10^m + 20^s \right)</math> | ||
These 20 seconds will correspond to the propagation time of sound from the lighthouse (transmitter) to the ship (receiver). The distance ρ between them can be obtained multiplying this value by the speed of sound v' 335 m/s. | These 20 seconds will correspond to the propagation time of sound from the lighthouse (transmitter) to the ship (receiver). The distance ρ between them can be obtained multiplying this value by the speed of sound <math>v' \simeq 335 m/s</math>. | ||
That is, ρ = 20 s * 335 m/s = 6:7 km. | That is, ρ = 20 s * 335 m/s = 6:7 km. | ||
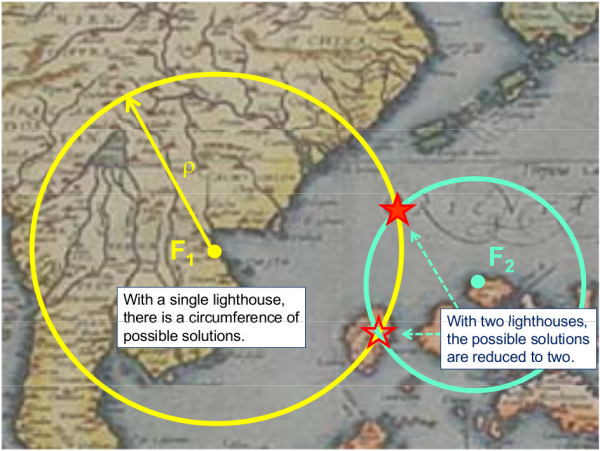
Obviously, with a single lighthouse it is only possible to determine a single measure of distance. So, the ship could be at any point over a circle of radius ρ, see figure 1.1. | Obviously, with a single lighthouse it is only possible to determine a single measure of distance. So, the ship could be at any point over a circle of radius ρ, see figure 1.1. | ||
Revision as of 20:35, 4 January 2011
The basic observable in a GNSS system is the time required for a signal to travel from the satellite (transmitter) to the receiver. This travelling time, multiplied by the speed of light, provides a measure of the apparent distance (pseudo range) between them. The following example summarises, for a two-dimensional case, the basic ideas involved in the GNSS positioning:
Let's suppose that a lighthouse is emitting acoustic signals at regular intervals of 10 minutes and intense enough to be heard some kilometres away. Let's also assume a ship with a clock perfectly synchronised with the one in the lighthouse, receiving these signals at a time not being an exact multiple of 10 minutes, for example, 20 seconds later [math]\displaystyle{ \left (t = n * 10^m + 20^s \right) }[/math] These 20 seconds will correspond to the propagation time of sound from the lighthouse (transmitter) to the ship (receiver). The distance ρ between them can be obtained multiplying this value by the speed of sound [math]\displaystyle{ v' \simeq 335 m/s }[/math]. That is, ρ = 20 s * 335 m/s = 6:7 km. Obviously, with a single lighthouse it is only possible to determine a single measure of distance. So, the ship could be at any point over a circle of radius ρ, see figure 1.1.
With a second lighthouse, the ship position will be given by the intersection of the two circumferences centred in the two lighthouses and radius determined by their distances to the ship (measured using the acoustic signals). In this case, the ship could be situated at any of the two points of intersection shown in figure 1.1. A third lighthouse will solve the previous ambiguity, nevertheless a rough knowledge of the ship position may allow us to proceed without the third lighthouse. For instance, in figure 1.1, one of the solutions falls on the ground (on an island).