If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor

Data Demodulation and Processing: Difference between revisions

From Navipedia
Jump to navigation Jump to search
Line 70: Line 70:


The pseudo-range to a given satellite, m, can be computed as (neglecting all propagation and equipment delays as well as noise):
The pseudo-range to a given satellite, m, can be computed as (neglecting all propagation and equipment delays as well as noise):
<math>\ro^m=c(T_U^m – T_S^m)</math>
<math>\rho^m=c(T_U^m - T_S^m)</math>


Where
Where
*<math>T_S</math> is the transmission time using the satellite clock, which has an error relatively to an absolute time reference (e.g. GPS time)
*<math>T_S</math> is the transmission time using the satellite clock, which has an error relatively to an absolute time reference (e.g. GPS time)
*<math>T_U</math> is the reception time using the receiver clock, which has an error relatively to an absolute time reference (e.g. GPS time)
*<math>T_U</math> is the reception time using the receiver clock, which has an error relatively to an absolute time reference (e.g. GPS time)
*c is the speed of light


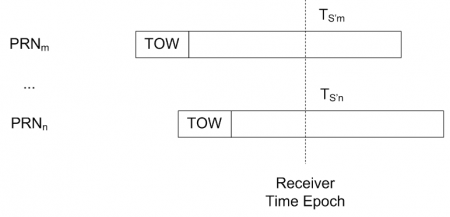
In reality, most GNSS receivers extrapolate the transmission time (at satellite clock) for all satellites at each receiver time epoch. Figure 2 illustrates this concept: <math>T_S’</math> are extrapolated for satellites m and n, where TOW is the time stamp recorded by the satellite at the beginning of each subframe.
In reality, most GNSS receivers extrapolate the transmission time (at satellite clock) for all satellites at each receiver time epoch. Figure 2 illustrates this concept: <math>T_S’</math> are extrapolated for satellites m and n, where TOW is the time stamp recorded by the satellite at the beginning of each subframe.




[[File:ddp_extrapol.png|center|thumb|650px|'''''Figure 2:''''' Extrapolation of transmission time at each receiver time epoch.]]
[[File:ddp_extrapol.png|center|thumb|450px|'''''Figure 2:''''' Extrapolation of transmission time at each receiver time epoch.]]




Line 86: Line 87:


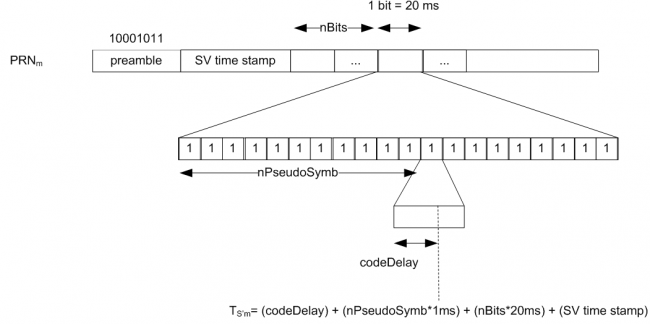
[[File:ddp_example.png|center|thumb|650px|'''''Figure 3:''''' Example of computation of extrapolated transmitted time.]]
[[File:ddp_example.png|center|thumb|650px|'''''Figure 3:''''' Example of computation of extrapolated transmitted time.]]


==Applications Processing==
==Applications Processing==

Revision as of 18:43, 4 May 2011


ReceiversReceivers
Title Data Demodulation and Processing
Author(s) GMV
Level Advanced
Year of Publication 2011
Logo GMV.png


While the tracking loops extract code and carrier information to synchronize the locally generated PRN code with the incoming signal, the Data demodulation and Processing block aims at extracting “useful information” to be used by the Applications Processing when generating a navigation solution. The core of this “useful information” consists on the navigation message and the observables, namely pseudo-range and Doppler frequency.


Concept

The inputs to the Data Demodulation and Processing block are the measurements from the tracking loops (code and carrier information) as well as the sign of the prompt correlator outputs. In fact, when a signal is being correctly tracked, the sign of the prompt correlator output is positive when the transmitted navigation symbol is 1 and negative when the symbol is -1, by definition of correlation.

The following nomenclature is used herein:

  • Pseudo-symbol: binary information corresponding to an excerpt of a symbol over a short time interval (e.g. one PRN code)
  • Symbol: binary information corresponding to the coded navigation message (e.g. for GPS L1 C/A symbols are the same as bits)
  • Bit: binary information corresponding to the navigation message


The process to extract the information necessary to compute a navigation solution consists in:

  • Synchronization: both at symbol and frame level
  • Data demodulation: to extract bits of the navigation message
  • Generation of basic observables


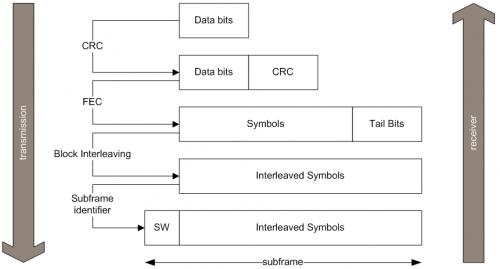
Figure 1 illustrates an example of how data is coded into the message structure, using the case of Galileo signals, where the subframe is the main element and frames are concatenations of subframes. Each step is further detailed in the following sections.


Figure 1: Example of a sequence of data de/modulation using the Galileo example.

Synchronization

Before achieving symbol synchronization, GNSS receivers often integrate the correlators over a period of a single PRN code.

  • Symbol Synchronization

For the case of GPS L1 C/A, where the PRN code duration is 1 ms and that 1 data bit lasts 20 ms, it means that there are 20 pseudo-bit in each bit. In order words, if the receiver is correctly tracking the signal, the sequence of pseudo-bits can be decomposed of bursts of 20 identical 1 (or -1) corresponding to a navigation message bit. Common resolve this ambiguity is to recur to histograms and counters to perform the so-called “bit synchronization” [1]. Please note that this nomenclature is valid for the GPS legacy signals (e.g. L1 C/A) but for most of the modernized signals, one should talk about “symbol synchronization”. After symbol synchronization is achieved, GNSS receivers typically increase the correlators integration times up to the symbol duration (e.g. 20 ms for GPS L1 C/A); and they start outputting (integrated) symbols, while checking that the histogram does not slip.

  • Frame Synchronization

Frame synchronization consists in finding out where are the frames from the sequence of symbols that the tracking loops are now providing. For the case of GPS L1 C/A, frame synchronization is achieved by looking for a preamble “10001011” which flags the beginning of all subframes of the navigation message; these preambles can be called Synchronization Words (SW).

At this point:

  • the receiver is able to retrieve the navigation message bits using the applicable SIS ICD, in case the message has no encoding, e.g. for GPS L1 C/A
  • the receiver is able to retrieve the symbols for each frame that still need to be decoded, in case the message used encoding, e.g. for Galileo Open Service

Data Demodulation

Data demodulation consists in extracting the bits of the navigation message with the maximum level of confidence. The steps required to achieve this goal actually depend on the signal at hand, and the applicable SIS ICD should be consulted on a case by case basis. Some of the techniques used are:

  • Parity Decoding: the parity of pre-defined sets of bits (e.g. words) is checked against a field containing the parity computed at transmission and sent within the navigation message. Any discrepancies would imply that there was at least one error in the transmission. This same concept is the basis for Cyclic Redundancy Checks (CRC).


  • Forward Error Correction (FEC): FEC encoding[2] consists in representing bits in more than one symbol, such that additional information is transmitted, allowing the receiver to detect and correct some potential errors, hence improving the performance of the channel. As an example, Galileo Open Service use forward error convolutional codes with a constraint length of 7 and a coding rate of 1/2 to spread the navigation message, i.e. one bit is codified as two symbols. Receivers may use Viterbi decoders[3] to recover the transmitted navigation message.


  • Block Interleaving: consists in transmitting the symbols in a different order. As an example, Galileo Open Service assembles the symbols in blocks of M columns x N rows and then transposes the block before sending the symbols in the SIS. The reverse operation needs to be conducted at the receiver in order to recover the transmitted symbols. The advantage of block interleaving is that it renders the message more robust to burst errors, since burst errors are now spread over a larger part of the message and may be still recoverable, e.g. using the FEC decoding techniques which have some capabilities to correct errors.

Generation of Basic Observables

At this point, the receiver is tracking the incoming signal and has extracted the navigation message, and therefore can compute the observables. Although Doppler frequency is quite straight forward and can be directly taken from the FLL or the instantaneous phase measured at the PLL, the pseudo-range still needs to be computed from the code delays values provided by the DLL.


The pseudo-range to a given satellite, m, can be computed as (neglecting all propagation and equipment delays as well as noise): [math]\displaystyle{ \rho^m=c(T_U^m - T_S^m) }[/math]

Where

  • [math]\displaystyle{ T_S }[/math] is the transmission time using the satellite clock, which has an error relatively to an absolute time reference (e.g. GPS time)
  • [math]\displaystyle{ T_U }[/math] is the reception time using the receiver clock, which has an error relatively to an absolute time reference (e.g. GPS time)
  • c is the speed of light

In reality, most GNSS receivers extrapolate the transmission time (at satellite clock) for all satellites at each receiver time epoch. Figure 2 illustrates this concept: [math]\displaystyle{ T_S’ }[/math] are extrapolated for satellites m and n, where TOW is the time stamp recorded by the satellite at the beginning of each subframe.


Figure 2: Extrapolation of transmission time at each receiver time epoch.


Figure 3 illustrates the computation of the extrapolated transmission time at the receiver, using the example of GPS L1 C/A, where 1 bit lasts 20 ms and each symbol lasts 1 ms. The code delay is the value output by the DLL.


Figure 3: Example of computation of extrapolated transmitted time.

Applications Processing

Finally, this information is passed to the Applications Processing block, which

Related articles

References

  1. ^ A. J. Van Dierendonck, “GPS Receivers”, from “Global Positioning System: Theory and Applications”, Volume I, Edited by B. W. Parkinson, J. J. Spilker Jr
  2. ^ http://en.wikipedia.org/wiki/Forward_error_correction
  3. ^ http://en.wikipedia.org/wiki/Viterbi_decoder
Retrieved from "https://gssc.esa.int/navipedia/index.php?title=Data_Demodulation_and_Processing&oldid=4093"