If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Front End: Difference between revisions
Rui.Sarnadas (talk | contribs) |
Rui.Sarnadas (talk | contribs) |
||
| Line 38: | Line 38: | ||
==Quantization and Sampling== | ==Quantization and Sampling== | ||
{| align="right" | |||
{| | |||
|- | |- | ||
| [[File:quantization.png| | | [[File:quantization.png|right|thumb|220px|'''''Figure 3:''''' Different quantization levels and approaches.]] | ||
| | | [[File:quantization_degradation.png|right|thumb|220px| '''''Figure 4:''''' Signal-to-Noise ratio degradation in quantization.]] | ||
| | |||
| | |||
|} | |} | ||
In analog to digital conversion there is an inherent ''quantization'' process, responsible for the output of a discrete digital quantity to an input signal value. | |||
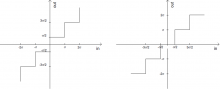
Different quantization methods, such as ''uniform'', ''non-uniform'', ''centered'', or ''non-centered'' (if there is no zero level) can be used, depending on the noise characteristics, as illustrated in Figure 3. Note that the ''Amoroso'' and ''DataFusion'' methods are non-uniform quantizers with different edges and quantized values, where ''P15'', ''P50'' (the ''median'') and ''P85'' are percentile values. | Different quantization methods, such as ''uniform'', ''non-uniform'', ''centered'', or ''non-centered'' (if there is no zero level) can be used, depending on the noise characteristics, as illustrated in Figure 3. Note that the ''Amoroso'' and ''DataFusion'' methods are non-uniform quantizers with different edges and quantized values, where ''P15'', ''P50'' (the ''median'') and ''P85'' are percentile values. | ||
The choice of quantization method and range depends on the noise characteristics. In GNSS receivers, the power levels of input signals are low, so the ADC quantization sees only noise-like signals at the input. Figure 4 shows the Signal-to-Noise Ratio (SNR) degradation, measured at a reciever's correlator output. In the figure, precorrelation bandwidth is neglected and infinite sampling rate is assumed, i.e. only the quantization process itself is taken into account. | The choice of quantization method and range depends on the noise characteristics. In GNSS receivers, the power levels of input signals are low, so the ADC quantization sees only noise-like signals at the input. Figure 4 shows the Signal-to-Noise Ratio (SNR) degradation, measured at a reciever's correlator output. In the figure, precorrelation bandwidth is neglected and infinite sampling rate is assumed, i.e. only the quantization process itself is taken into account. | ||
A uniform quantization with <math>k\,</math> bits has <math>2k-1\,</math> edges, and these quantization edges (thresholds) must be optimized in terms of the noise variance <math>\sigma\,</math>, given by <math>k=L / \sigma\,</math> | A uniform quantization with <math>k\,</math> bits has <math>2k-1\,</math> edges, and these quantization edges (thresholds) must be optimized in terms of the noise variance <math>\sigma\,</math>, given by: | ||
<math>k=L / \sigma\,</math> | |||
[[File:nyquist_and_aliasing.png|right|thumb| | As for the number of bits to use, it can be seen from Figure 4 that signal degradation when using 2-bit quantization is about 1.5 dB, increasing to 3.5 dB when using 1-bit quantization. For GNSS signals and receivers, however, these are quite affordable losses for decreasing the number of quantization bits. Although using 1-bit data also discards the need for an AGC, therefore simplifying the hardware, enabling gain control through an AGC system may still help in interference mitigation. | ||
When the ADC samples the input signal (typicaly at a lower IF frequency after down-conversion), the ''sampling frequency'' <math>f_s\,</math> should be carefuly chosen. In fact, for GNSS signals, <math>f_s\,</math> should not be a multiple of | [[File:nyquist_and_aliasing.png|right|thumb|220px|'''''Figure 5:''''' Illustration of Nyquist theorem and aliasing effects.]] | ||
When the ADC samples the input signal (typicaly at a lower IF frequency after down-conversion), the ''sampling frequency'' <math>f_s\,</math> should be carefuly chosen. In fact, for GNSS signals, <math>f_s\,</math> should not be a multiple of 10.23 MHz, since this is the fundamental frequency in GNSS signal generation, as shown [[GPS signal description|here]]. As stated by the Nyquist–Shannon sampling theorem<ref>[[wikipedia:Nyquist–Shannon sampling theorem]]</ref>, the sampling frequency <math>f_s\,</math>, needed to represent and reproduce the signal, is related to the one-sided baseband bandwith <math>B\,</math> by: | |||
Revision as of 16:00, 8 April 2011
| Receivers | |
|---|---|
| Title | Front End |
| Author(s) | GMV |
| Level | Advanced |
| Year of Publication | 2011 |
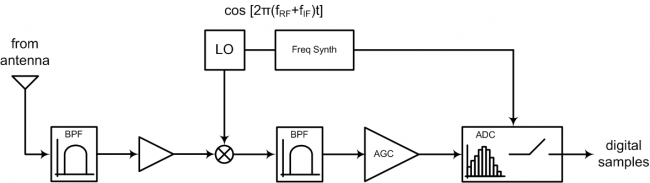
A GNSS signal is captured through the receiver's antenna, and is fed to the front end section. The front end is then responsible for "preparing" the received signals for signal processing tasks, and many different implementations can achieve the desired results. As allways, some requirement and trade-off analysis is needed when designing a front-end for GNSS receivers, depending on the application at hand. Figure 1 illustrates a typical front end structure in GNSS receivers.
Within a front end, the frequency synthesizer (shown in Figure 1) is the heart, by providing the receiver time and frequency reference for all the components. Such components, at front end architecture level, gather typical interconnected steps to process and convert a RF signal to a baseband digital signal:
- Filtering and amplification: these stages are necessary to ensure low noise and out-of-band rejection in the received signals, as well as amplification stages to compensate for transmission losses.
- Down-conversion: The front end is responsible for down-converting the signal, whether using direct conversion[1] techniques, to convert the RF spectrum directly to baseband, or heterodyning[2] approaches, where typically a multi-stage approach is used to shift the spectrum to intermediate frequencies (IF), with the appropriate band filtering, ultimately converting the IF signals to baseband[3].
- Quantization: The incoming signals are ditized through analog to digital converters[4] (ADC), ensuring that quantization errors and dynamic ranges are appropriate to accomodate the signal's characteristics.
- Automatic Gain Control: The automatic gain control[5] (AGC) stage is closely related to the down-conversion and quantization steps, and is responsible for adjusting the gain of the front end section to an appropriate level, in terms of the signal's range of input and output levels.
These operations and different stages in front end signal processing are described in the following sections.
Filtering and Amplification
Due to the GNSS signal's low power upon reception, there is usually a set of filtering and low-noise amplification stages after the antenna. Although the implementation itself varies between architectures and hardware realizations, the principle is the same: the signal is amplified, keeping the noise figure low and rejecting possible out-of-band interference. This can be achieved by interleaving Low-Noise Amplifiers (LNA) and filter stages. For more details on amplification, filtering and losses see the antenna section.
Down-conversion
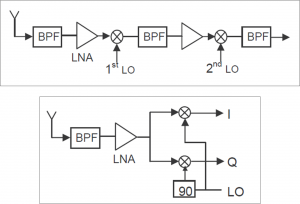
The down-conversion stage's main objective is to convert the input signal from RF to IF and / or to baseband (possibly after a pre-amplification stage). This is achieved through signal mixing operations, such as homodyning and heterodyning, which consist in mixing two different frequency signals in order to generate the same information at two different frequencies, where one is the sum of the two frequencies mixed, and the other is their difference. The basis of the mixing process is the local oscilator (LO), which must be carefully chosen to avoid harmonics and image frequencies near IF. Examples of homodyne and heterodyne mixers are shown in Figure 2.
Heterodyne implementations are the most common. There is typically a two-stage approach, where these multiple stages down-convert the signals to different IF, leading to large separation of image frequencies[6]. Furthermore, this multi-stage design allows for lower quality factor filters, where different trade-offs and fine tunning of derived architectures is more flexible (e.g. the superheterodyne approach). The success of heterodyning is mainly due to the fact that the resulting IF spectrum (lower frequencies than IF) allows for lower cost ADC stages, while using lower quality factor filters. Also, the multi-stage approach enables further filtering of out of band noise and interference, as well as rejection of unwanted frequency images.
For the case of homodyne mixers, there is only a single stage of signal down-conversion, and the local oscilator is tunned at RF. This approach is often reffered to as direct conversion, since the mixing at RF converts the RF spectrum directly to baseband. Although an atractive solution, since it eliminates the need for intermediate filters like image frequency removal, direct conversion is chalenging due to the need of filters with high quality factors (i.e. increased cost and performance). Another problem is that down-converting directly to baseband shifts harmonics close to zero, making them difficult to filter out.
One topic that is often introduced while discussing down-conversion is direct sampling. Direct RF sampling means exactly that: signal are sampled directly at RF, without down-conversion stages. Althouth this approach discards mixers and LO in the design, it also requires amplifiers and ADC to operate at RF. As technology goes, hardware components at RF level (around 1.2 GHz to 1.6 GHz) are impratical for mass market applications, for design and component costs. Despite the difficulty to design and implement, direct sampling strategies have their advantages: in the down-conversion stages where an oscilator is present, mixers introduce unwanted signals, and any mismatch of the LO leads to errors. Also, direct sampling yields reduced sensitivity to clock jitter and noise folding, and the same front-end can be used for all GNSS signals.
Quantization and Sampling
In analog to digital conversion there is an inherent quantization process, responsible for the output of a discrete digital quantity to an input signal value. Different quantization methods, such as uniform, non-uniform, centered, or non-centered (if there is no zero level) can be used, depending on the noise characteristics, as illustrated in Figure 3. Note that the Amoroso and DataFusion methods are non-uniform quantizers with different edges and quantized values, where P15, P50 (the median) and P85 are percentile values.
The choice of quantization method and range depends on the noise characteristics. In GNSS receivers, the power levels of input signals are low, so the ADC quantization sees only noise-like signals at the input. Figure 4 shows the Signal-to-Noise Ratio (SNR) degradation, measured at a reciever's correlator output. In the figure, precorrelation bandwidth is neglected and infinite sampling rate is assumed, i.e. only the quantization process itself is taken into account.
A uniform quantization with [math]\displaystyle{ k\, }[/math] bits has [math]\displaystyle{ 2k-1\, }[/math] edges, and these quantization edges (thresholds) must be optimized in terms of the noise variance [math]\displaystyle{ \sigma\, }[/math], given by:
[math]\displaystyle{ k=L / \sigma\, }[/math]
As for the number of bits to use, it can be seen from Figure 4 that signal degradation when using 2-bit quantization is about 1.5 dB, increasing to 3.5 dB when using 1-bit quantization. For GNSS signals and receivers, however, these are quite affordable losses for decreasing the number of quantization bits. Although using 1-bit data also discards the need for an AGC, therefore simplifying the hardware, enabling gain control through an AGC system may still help in interference mitigation.
When the ADC samples the input signal (typicaly at a lower IF frequency after down-conversion), the sampling frequency [math]\displaystyle{ f_s\, }[/math] should be carefuly chosen. In fact, for GNSS signals, [math]\displaystyle{ f_s\, }[/math] should not be a multiple of 10.23 MHz, since this is the fundamental frequency in GNSS signal generation, as shown here. As stated by the Nyquist–Shannon sampling theorem[7], the sampling frequency [math]\displaystyle{ f_s\, }[/math], needed to represent and reproduce the signal, is related to the one-sided baseband bandwith [math]\displaystyle{ B\, }[/math] by:
[math]\displaystyle{ f_s \gt 2 B\, }[/math]
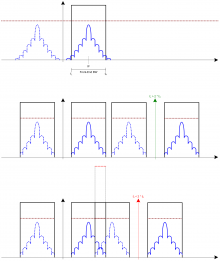
The sampling process can also be seen as shifting an placing the [math]\displaystyle{ 0\, }[/math] (zero) frequency over [math]\displaystyle{ N\, }[/math] frequencies, given by:
[math]\displaystyle{ \pm N \times f_s, N \in \mathbb{Z}\, }[/math]
In other words, the signal center frequency and spectrum is shifted and added [math]\displaystyle{ N\, }[/math] times over the full spectrum. The resulting replicas at [math]\displaystyle{ \pm N \times f_s\, }[/math] must not overlap to avoid aliasing[8] effects. These sampling effects are illustrated in Figure 5.
Automatic Gain Control
From RF to Baseband
Related articles
References
- ^ http://www.gpsworld.com/gnss-system/galileo/pulling-wideband-7053
- ^ wikipedia:Heterodyne receiver
- ^ wikipedia:Digital down converter
- ^ wikipedia:Analog-to-digital converter
- ^ wikipedia:Automatic gain control
- ^ wikipedia:Image frequency
- ^ wikipedia:Nyquist–Shannon sampling theorem
- ^ wikipedia:Aliasing