If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Electromagnetic Beam Bending: Difference between revisions
Carlos.Lopez (talk | contribs) No edit summary |
m (fixed broken link.) |
||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{Article Infobox2 | {{Article Infobox2 | ||
|Category=Fundamentals | |Category=Fundamentals | ||
|Authors=J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. | |||
|Authors=J. Sanz Subirana, | |||
|Level=Basic | |Level=Basic | ||
|YearOfPublication=2011 | |YearOfPublication=2011 | ||
|Title={{PAGENAME}} | |||
}} | }} | ||
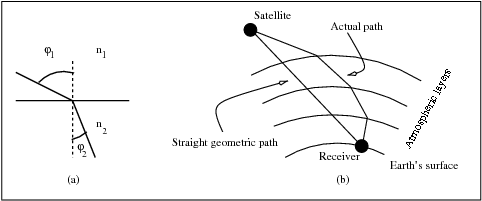
As it is known, the density of the atmospheric gas and plasma is not homogeneous. This causes spatial and temporal variations in the refraction index. Due to the refractive index gradients, the rays suffer an excess of geometric path, regarding to the free space path, when crossing the atmosphere. The Snell's law states that if an electromagnetic wave travels from an environment with refractive index <math>n_1</math> to a second one with refractive index <math>n_2</math> and crosses the separation between them with an angle <math>\varphi_1</math>, it will be deviated with an angle <math>\varphi_2</math>. The relation between these four values is summarised by the expression: <math>n_1 \cdot \sin \varphi_1 = n_2 \cdot \sin \varphi_2</math>. | As it is known, the density of the atmospheric gas and plasma is not homogeneous. This causes spatial and temporal variations in the refraction index. Due to the refractive index gradients, the rays suffer an excess of geometric path, regarding to the free space path, when crossing the atmosphere. The Snell's law states that if an electromagnetic wave travels from an environment with refractive index <math>n_1</math> to a second one with refractive index <math>n_2</math> and crosses the separation between them with an angle <math>\varphi_1</math>, it will be deviated with an angle <math>\varphi_2</math>. The relation between these four values is summarised by the expression: <math>n_1 \cdot \sin \varphi_1 = n_2 \cdot \sin \varphi_2</math>. | ||
| Line 12: | Line 12: | ||
Figure 1(a) illustrates this basic postulate: <math>\varphi_2 < \varphi_1</math> because <math>n_2 > n_1</math>. The consequence of this law can be seen in Figure 1(b), the successive trespasses of different layers, each one with its own refractive index, | Figure 1(a) illustrates this basic postulate: <math>\varphi_2 < \varphi_1</math> because <math>n_2 > n_1</math>. The consequence of this law can be seen in Figure 1(b), the successive trespasses of different layers, each one with its own refractive index, cause a curvature in the ray path that causes a delay as discussed above. | ||
For the Troposphere (see [Parkinson et al., 1996]<ref>[Parkinson et al., 1996] Parkinson, B., Spilker, J. and Enge, P., 1996. Global Positioning System, Vol. I and II. Theory and Applications. American Institute of Aeronautics, USA.</ref>), the effect caused by neglecting path curvature is less than <math>3</math> millimetres for elevations greater than <math>20</math> degrees, <math>2</math> centimetres for elevations close to <math>10</math> degrees and increases to <math>17</math> centimetres at elevations close to <math>5</math> degrees (mainly due to dry gases). | For the Troposphere (see [Parkinson et al., 1996]<ref>[Parkinson et al., 1996] Parkinson, B., Spilker, J. and Enge, P., 1996. Global Positioning System, Vol. I and II. Theory and Applications. American Institute of Aeronautics, USA.</ref>), the effect caused by neglecting path curvature is less than <math>3</math> millimetres for elevations greater than <math>20</math> degrees, <math>2</math> centimetres for elevations close to <math>10</math> degrees and increases to <math>17</math> centimetres at elevations close to <math>5</math> degrees (mainly due to dry gases). | ||
For the Ionosphere, these errors can reach up to few centimetres for L1 and L2 GPS signals [Hoque and Jakowsky, 2008]<ref> [Hoque and Jakowsky, 2008] Hoque, M. and Jakowsky, N., 2008. Estimate of higher order ionospheric errors in GNSS positioning. Radio Science. 43,pp. 1-15. </ref>, at low elevations and under high solar activity conditions. | For the Ionosphere, these errors can reach up to few centimetres for L1 and L2 GPS signals [Hoque and Jakowsky, 2008]<ref> [Hoque and Jakowsky, 2008] Hoque, M. and Jakowsky, N., 2008. Estimate of higher order ionospheric errors in GNSS positioning. Radio Science. 43,pp. 1-15. </ref>, at low elevations and under high solar activity conditions. On the other hand the bending angle is proportional to the inverse of the squared frequency and mostly cancels in the ionosphere-free combination <ref> Hajj, G., Kursinsky, E., Romans, L., Bertier, W. and Leroy, S., 2002. A technical description of atmospheric sounding by GPS occultation. Journal of Atmospheric and Solar-Terrestrial Physics 64, pp. 451–469 </ref> (see also the tutorial <ref> Sanz, J., Juan, J. and Hernandez-Pajares, M., 2012. Analysis of propagation effects from GNSS observables based on laboratory exercises. Course on Propagation effects, channel models and related error sources on GNSS, ESA/ESAC., Madrid, Spain. http://gage.upc.edu/tutorials</ref>). | ||
Latest revision as of 17:00, 8 September 2014
| Fundamentals | |
|---|---|
| Title | Electromagnetic Beam Bending |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
As it is known, the density of the atmospheric gas and plasma is not homogeneous. This causes spatial and temporal variations in the refraction index. Due to the refractive index gradients, the rays suffer an excess of geometric path, regarding to the free space path, when crossing the atmosphere. The Snell's law states that if an electromagnetic wave travels from an environment with refractive index [math]\displaystyle{ n_1 }[/math] to a second one with refractive index [math]\displaystyle{ n_2 }[/math] and crosses the separation between them with an angle [math]\displaystyle{ \varphi_1 }[/math], it will be deviated with an angle [math]\displaystyle{ \varphi_2 }[/math]. The relation between these four values is summarised by the expression: [math]\displaystyle{ n_1 \cdot \sin \varphi_1 = n_2 \cdot \sin \varphi_2 }[/math].
Figure 1(a) illustrates this basic postulate: [math]\displaystyle{ \varphi_2 \lt \varphi_1 }[/math] because [math]\displaystyle{ n_2 \gt n_1 }[/math]. The consequence of this law can be seen in Figure 1(b), the successive trespasses of different layers, each one with its own refractive index, cause a curvature in the ray path that causes a delay as discussed above.
For the Troposphere (see [Parkinson et al., 1996][1]), the effect caused by neglecting path curvature is less than [math]\displaystyle{ 3 }[/math] millimetres for elevations greater than [math]\displaystyle{ 20 }[/math] degrees, [math]\displaystyle{ 2 }[/math] centimetres for elevations close to [math]\displaystyle{ 10 }[/math] degrees and increases to [math]\displaystyle{ 17 }[/math] centimetres at elevations close to [math]\displaystyle{ 5 }[/math] degrees (mainly due to dry gases).
For the Ionosphere, these errors can reach up to few centimetres for L1 and L2 GPS signals [Hoque and Jakowsky, 2008][2], at low elevations and under high solar activity conditions. On the other hand the bending angle is proportional to the inverse of the squared frequency and mostly cancels in the ionosphere-free combination [3] (see also the tutorial [4]).
References
- ^ [Parkinson et al., 1996] Parkinson, B., Spilker, J. and Enge, P., 1996. Global Positioning System, Vol. I and II. Theory and Applications. American Institute of Aeronautics, USA.
- ^ [Hoque and Jakowsky, 2008] Hoque, M. and Jakowsky, N., 2008. Estimate of higher order ionospheric errors in GNSS positioning. Radio Science. 43,pp. 1-15.
- ^ Hajj, G., Kursinsky, E., Romans, L., Bertier, W. and Leroy, S., 2002. A technical description of atmospheric sounding by GPS occultation. Journal of Atmospheric and Solar-Terrestrial Physics 64, pp. 451–469
- ^ Sanz, J., Juan, J. and Hernandez-Pajares, M., 2012. Analysis of propagation effects from GNSS observables based on laboratory exercises. Course on Propagation effects, channel models and related error sources on GNSS, ESA/ESAC., Madrid, Spain. http://gage.upc.edu/tutorials